线性调频信号高耦合系数条件下的目标跟踪

黄 强，王建卫

(南京电子技术研究所， 南京210039)

0 引言

线性调频信号具有诸多优点，例如通过相位调制可以获得大时宽带宽积，匹配滤波对多普勒频移不敏感等［1］。因此，线性调频信号被广泛应用于雷达领域。但线性调频信号经过脉冲压缩后具有很强的距离多普勒效应，使得距离量测有一定偏差(偏差与径向速度和耦合系数有关)，为后续的目标状态估计和数据互联带来较大的影响。

为了解决这个问题，国内外很多学者采用了测速的方法［2-3］，但该方法有很大的局限性，无法在工程中应用。另外纯粹数据处理的方法是先不考虑距离耦合的影响，使用Kalman滤波器在有距离偏移的情况下进行滤波，然后根据滤波估计的径向速度和距离多普勒耦合系数对距离进行修正。该方法在低耦合系数(且耦合系数较小变化)和低速目标情况下是适用的。但在高耦合系数和高速目标情况下，经过该方法修正后的距离依然存在着较大偏差。文献［4-5］采用带有径向速度的扩展卡尔曼滤波(Extend Kalman Filter，EKF)方法，该方法需要具有径向速度测量量，但在实际情况下很难测得径向速度。文献［6-7］中，在极坐标系下滤波，距离维量测中不改变径向速度带来的距离走动，在一定程度上改善了距离估计精度。为此本文把该方法推广到直角坐标系，采用EKF和不敏卡尔曼滤波(Unsented Transformation Kalman Filter，UKF)的方法进行带距离多普勒耦合距离走动的滤波，最后通过仿真，分析了几种方法的优缺点，并给出了相应结论。

1 问题的描述

对于线性调频信号，当目标存在径向速度时，就会发生多普勒失配现象。也就是匹配滤波器输出的峰值并非出现在期望的t=0时刻。相反，峰值输出位置的移动量与多普勒频移成比例。由于对目标距离的估计是基于该峰值出现的时间，所以多普勒失配将引起测距误差。相应的距离误差为

式中:f0为发射信号的中心频率;τ为脉冲宽度;v为目标径向速度;B为信号带宽。从式(1)中可以看出，线性调频信号多普勒失配引起的测距误差和中心频率、脉冲宽度和目标速度成正比，和信号带宽成反比。定义多普勒耦合系数为

下面给出不同波段雷达距离误差计算，参见表1。

表1 不同波段雷达距离误差

从表1可以看出，对于远距离高速目标，不同频段造成的距离误差从百米到十公里量级，差别较大。对于远程弹道导弹和卫星的运动速度要远远大于2 km/s，造成的距离误差将成倍的增加。如果目标的径向速度恒定不变，则采用先估计速度再距离修正不会存在太大的问题。但往往轨道目标的运动速度相对于观测站变化剧烈，采用该方法修正后的距离依然存在着较大偏差。下面以示例说明:图1为采用STK软件生成的某高速目标的径向速度曲线;图2为采用先估计径向速度再修正距离误差的距离精度(假定多普勒耦合系数为2)。

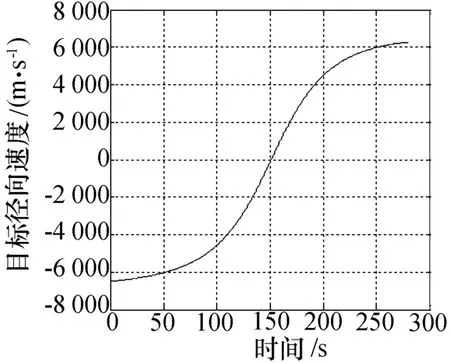
图1 目标径向速度随时间变化曲线

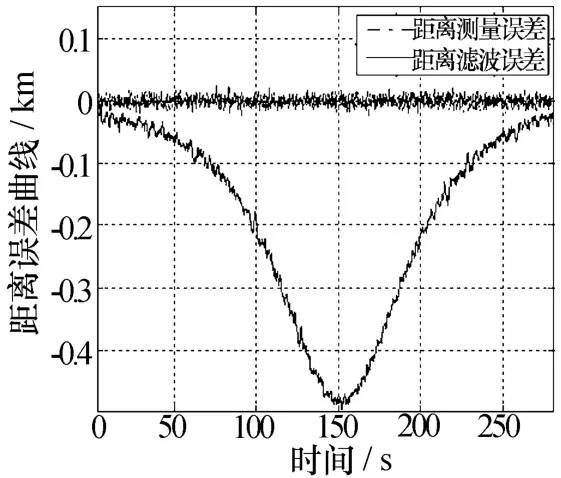
图2 先估计后修正的距离误差

从图2可以看出，在目标径向速度变化最大时(150 s)修正后的距离误差最大，达到了近0.5 km。也就是说，对于高速目标和高耦合系数条件下，采用先估计再修正的方法已经不再适用，因此需要采用新方法来解决这个问题。

2 滤波新算法

以往的算法都是在估计出目标径向速度后修正距离走动误差，这对较小耦合系数和较低速度目标是适用的，但对高耦合系数和高速目标已不再适用。下面介绍本文的新方法。

2.1 极坐标滤波算法

假定目标在距离维独立滤波。目标的运动方程如下

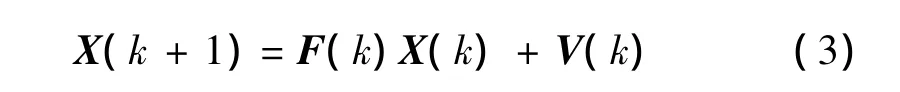
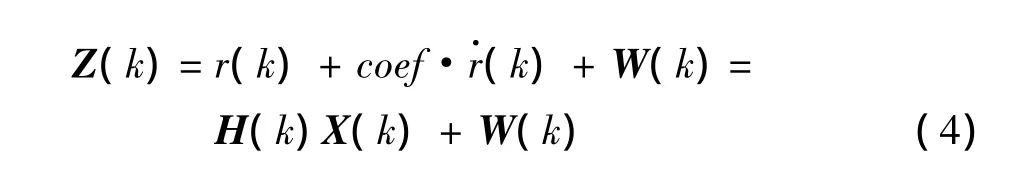
式中:coef为耦合系数，可参考式(2);H(k)=［1，coef，0］，W(k)为具有协方差R(k)(1×1矩阵)的零均值，白色高斯量测噪声序列。

从式(4)可以看出，其和常规量测方程唯一差别就是H矩阵中第二项是耦合系数coef，而不是零。滤波方法和常规的线性卡尔曼滤波方法相同，可以参考文献［8］。

2.2 直角坐标EKF和UKF滤波算法

如果目标的状态在直角坐标系下描述，就需要采用非线性滤波的方法。下面介绍基于EKF和UKF滤波的算法。目标在直角坐标系下的运动方程可以描述为

式中:Z(k)=［r(k)，a(k)，e(k)］T，分别为目标距离、方位和仰角。W(k)为具有协方差R(k)(3×3矩阵)的零均值，白色高斯量测噪声序列。h(k，X(k))如下式

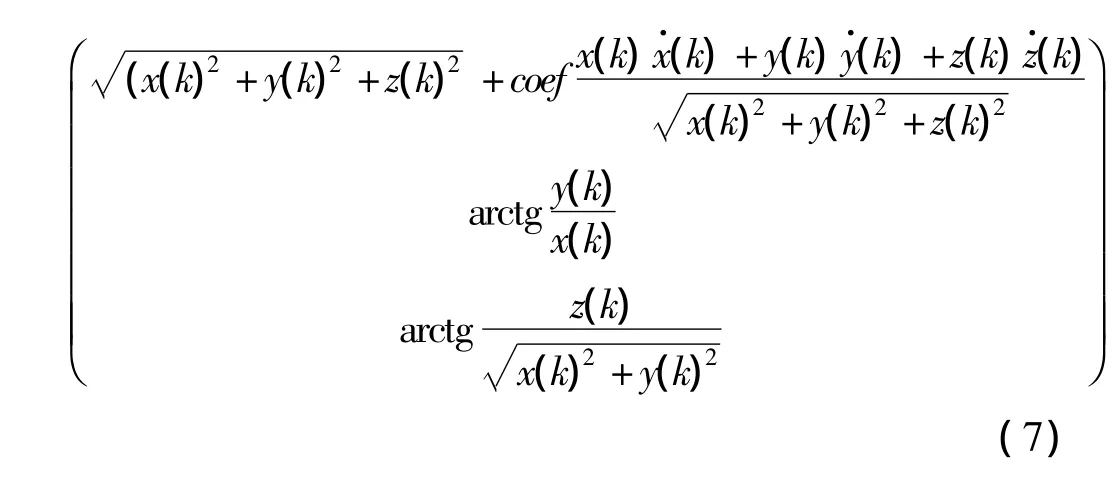
对于EKF滤波算法，其本质上就是把非线性问题线性化(泰勒展开)，然后采用线性滤波的方法来进行滤波。对于本文方法的EKF滤波需要计算量测方程式(7)的3×9雅可比矩阵H，其非零元素计算如下

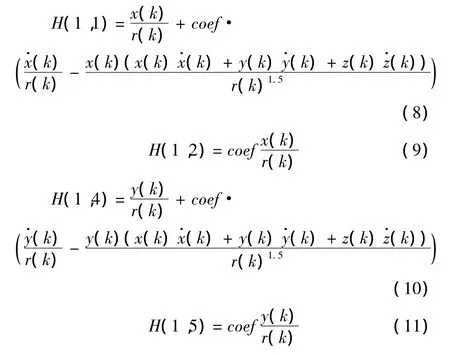
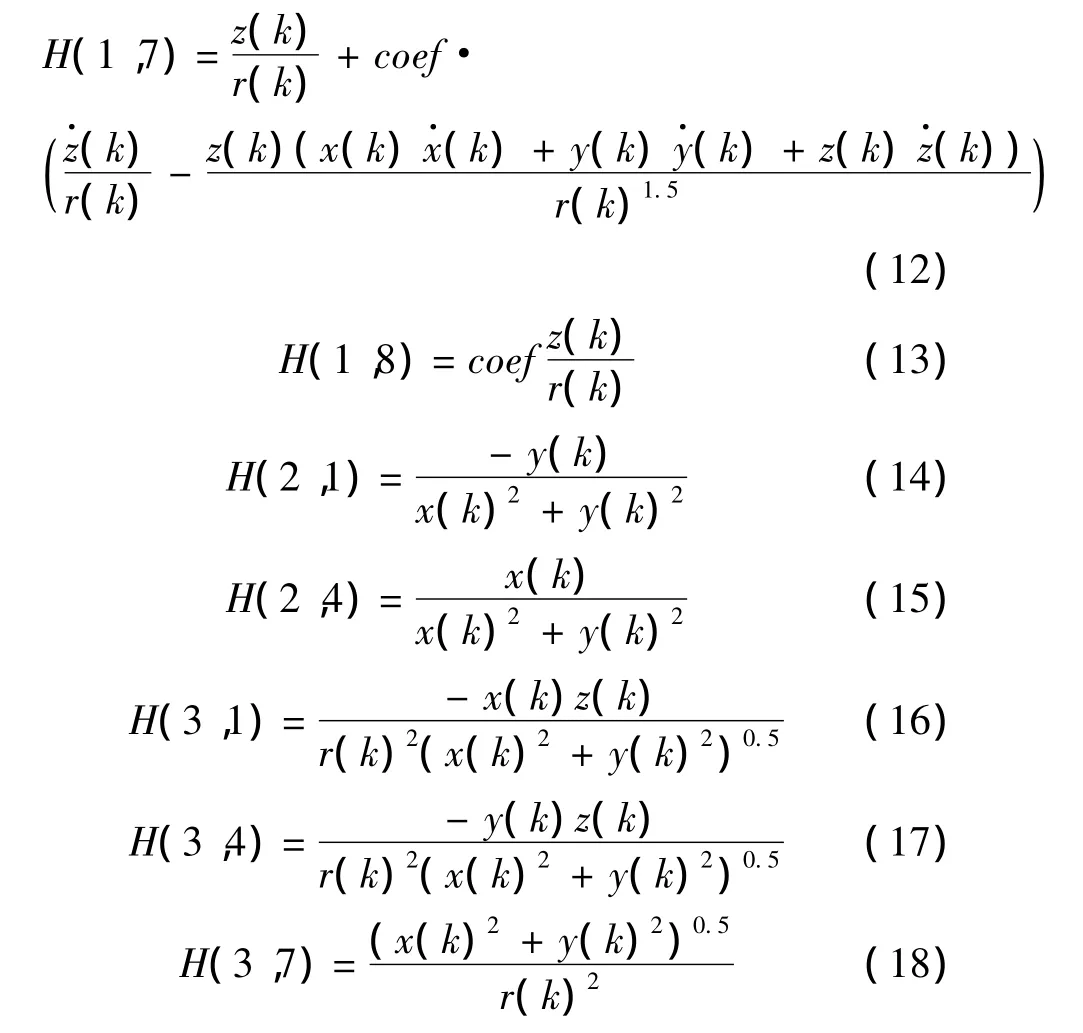
根据预测向量可以计算得到当前时刻的雅可比矩阵H，就可以套用线性滤波方法进行EKF滤波，具体方法可以参考文献［8］。

而另外一种对付非线性滤波的方法就是UKF，UKF是在不敏变换(Unsented Transformation，UT)基础上发展起来的，其精度相当于二阶泰勒展开的精度，其运算量远远大于EKF的运算量。由于其在对付非线性方面的优良特性，使其也在工程中得到了广泛应用。UKF应用于距离走动的直角坐标系滤波中，改动相对较少，只需要考虑距离量测方程中的多普勒失配带来的距离误差项即可(参考式(7))，具体的UKF滤波算法可以参考文献［8］。

3 仿真分析

下面分别采用本文提出的3种方法进行仿真分析，比较3种方法的滤波精度。目标采用STK软件产生的弹道导弹数据，其径向速度曲线参考图1。假定雷达的测距精度7 m，测角精度3 mrad，采样数据率为0.1 s，距离走动系数为2，目标运动模型采用singer模型。图3为极坐标系滤波结果，图4为直角坐标系EKF滤波结果，图5为直角坐标系UKF滤波结果。表2为3种滤波方法的精度对比分析结果。

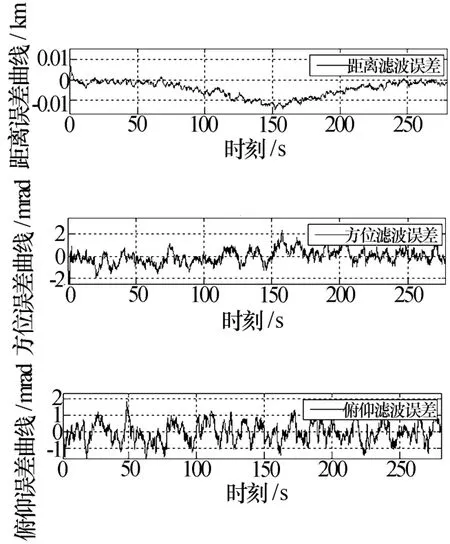
图3 极坐标系滤波结果

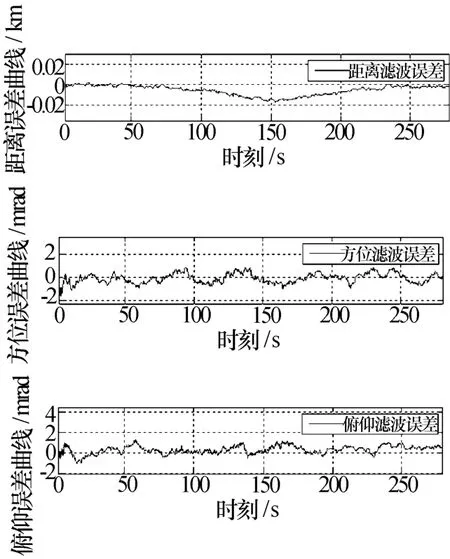
图4 直角坐标系EKF滤波结果

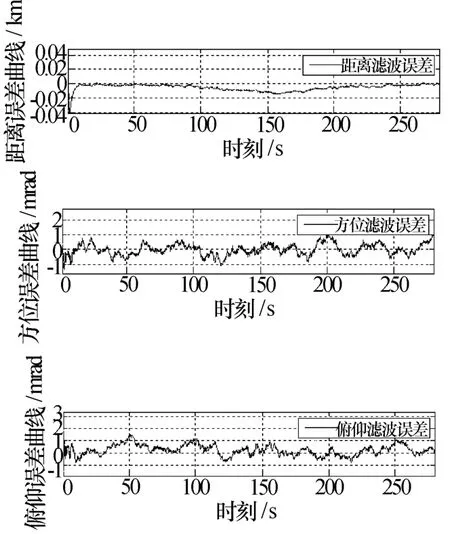
图5 直角坐标系UKF滤波结果

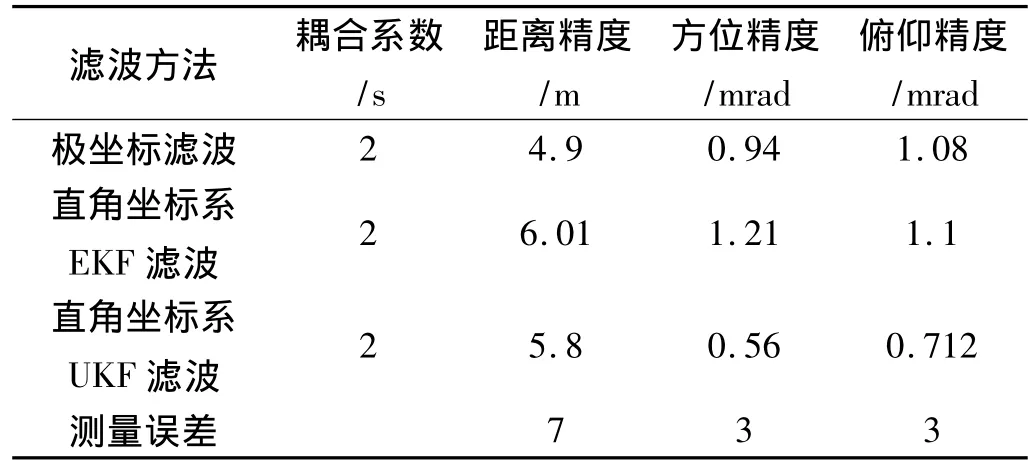
表2 不同滤波方法的滤波精度

从图3、图4、图5和表2可以看出，在考虑高耦合系数条件下极坐标系滤波距离精度最高，其次为UKF，EKF最差;角精度UKF最高，其次为极坐标系三维解耦滤波，EKF最差。主要原因是距离量测方程中加入了耦合误差项，使得非线性加强，导致了EKF滤波精度的下降，同时也说明了UKF对付非线性滤波问题的有效性。从以上分析可知，如果受限于运算资源并需要保证一定的滤波精度，可以采用极坐标系下三维解耦滤波算法;如果不受运算资源的限制，可以在工程应用中采用UKF滤波算法。

4 结束语

为了解决高频段雷达在跟踪高速目标过程中，由于采用线性调频信号带来的多普勒失配距离偏差，本文采用不改变距离量测方程，也就是不破坏量测方程的可观测性，分别给出了极坐标系三维解耦滤波、直角坐标系EKF滤波和直角坐标系UKF滤波算法。最后通过仿真验证了在高耦合系数条件下本文算法的有效性和相应的适用条件，同时给出了3种滤波方法的精度对比分析结果。在工程实践中将会遇到各种各样的问题和不同的需求，因此在工程中采用什么算法还要根据实际情况来定。本文的高耦合系数条件下的滤波算法可供应用时参考。

［1］ 向敬成.雷达系统［M］.北京:电子工业出版社，2001.Xiang Jingcheng.Radar systems［M］.Beijing:Publishing House of Electronics Industry，2001.

［2］ 赵 锋，王雪松，肖顺平.高耦合系数条件下径向速度估计的新方法［J］.电子学报，2005，9(33):1571-1575.Zhao Feng，Wang Xuesong，Xiao Shunping.A new method of radial velocity estimation for high coupling coeficient［J］.Acta Electronica Sinica，2005，9(33):1571-1575.

［3］ Abatzoglou T J，et al.Range，radial velocity，and acceleration MLE using radar LFM pulse train［J］.IEEE Transactions on Aerospace and Electronic Systems，1998，34(4):107l-1083.

［4］ 王建国，何佩琨，龙 腾.径向速度测量在Kalman滤波中的应用［J］.北京理工大学学报，2002，22(2):225-227.Wang Jianguo，He Peikun，Long Teng.Use of radial velocity measurements in Kalman filter［J］.Journal of Beijing Institute of Technology，2002，22(2):225-227.

［5］ 王建国，龙 腾，何佩琨.一种线性调频波形下的目标跟踪算法［J］.现代雷达，2003，2(25):26-29.Wang Jianguo，Long Teng，He Peikun.A target tracking algorithm with LFM waveforms［J］.Morden Radar，2003，2(25):26-29.

［6］ Fitzgerald R J.Effect of range-Doppler coupling on chirp radar tracking accuracy［J］.IEEE Transactions on Aerospace and Electronic Systems，1974，10(4):528-532.

［7］ Wong W.Blair W D.Steady state tracking with LFM waveforms［J］.IEEE Transactions on Aerospace and Electronic Systems，2000，36(2):701-709.

［8］ 何 友，修建娟，张晶炜，等.雷达数据处理及应用［M］.北京:电子工业出版社，2006.He You，Xiu Jianjuan，Zhang Jingwei，et al.Radar data processing with applications［M］.Beijing:Publishing House of Electronics Industry，2006.