相控阵天线瞬时带宽扩展方法研究

郑小雨，刘洛琨，郭 虹，杨金金

(解放军信息工程大学信息系统工程学院， 郑州450002)

0 引言

相控阵天线主要应用于雷达、通信、电子对抗等系统中。随着需求的提高，近些年来，这些应用系统已逐步转变为宽带系统［1］。因此，相控阵天线也应具备大瞬时带宽的工作能力。传统的阵列在每个阵元采用移相器(Phase Shifter，PS)实现空域波束扫描。但当阵列接收宽带信号时，会出现波束指向漂移现象［2］。除此之外，当阵列孔径过大时，由于孔径渡越时间的影响，阵列合成信号将会有所损失或合成波形展宽［3］。为了克服以上问题，许多学者针对如何扩展阵列瞬时带宽进行了深入的研究［4-7］。现阶段，相控阵天线多采用实时延时(TrueTimeDelay，TTD)技术以实现系统大瞬时带宽的要求［8-9］。

如果在阵元级加入TTD，由于所需设备数量众多，会引起系统复杂度及成本的增加，同时，延时线由于精度有限，其量化误差也会使输出波形畸变。因此，在包含多个阵元的子阵级使用TTD，可以大幅度减少设备数量，并且量化误差可以由阵元级PS在中心频点进行近似补偿［9］。

本文对相控阵天线瞬时带宽进行了研究。

1 瞬时带宽的限制因素

相控阵天线瞬时带宽的限制因素主要有以下两点:第一，阵列采用移相器控制波束扫描，并且通常是以信号的中心频率设计移相器的波控码控制天线波束的指向。当接收信号具有一定的带宽时，频率会偏离中心频率，若控制移相器的波控码不变，那么移相器提供的相位权将会保持不变，这就导致波束扫描的指向发生偏离，我们将这种随信号频率变化而引起的波束在空间上角度指向偏离的现象称为空间色散。第二，相控阵天线在接收宽带宽角信号时，由于孔径渡越时间的限制，阵列两端天线单元所接收到的信号将不能同时相加，这种由于宽带信号在宽角扫描所引起的信号合成损失或波形展宽现象称为时间色散。

下面，我们具体分析空间色散与时间色散对阵列瞬时带宽的影响。为了便于后面的讨论，下面给出一个未划分线阵的结构框图，如图1所示。其中，阵元数为M，每个阵元使用数字移相器实现波束扫描。

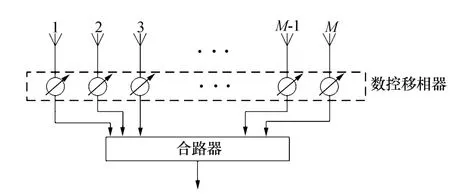
图1 使用数字移相器的均匀线阵结构图

1.1 空间色散

正如前文所述，阵列实现波束扫描是通过改变每一路天线的相位补偿实现的。先假定工作频率为接收信号的中心频率f0，若要实现天线阵列波束指向θB，则每个天线单元由移相器提供的相位补偿应为

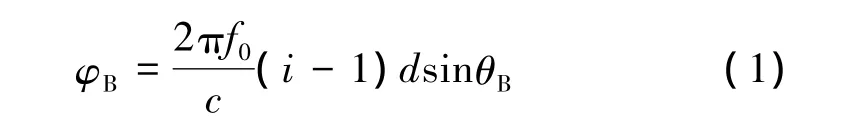
式中:i=1，2，…，M;d为阵元间距;c为真空中的光速。φB会比2π大很多，而移相器所提供的相移值一般小于2π。因此，移相器所提供的相移可由式(2)求得

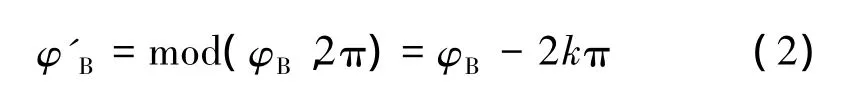
式中:k=0，±1，±2，…;mod(·)表示取模运算。移相器所提供的相移值不随频率变化，当接收信号的频率由f0变为f0+Δf时，阵列理想的相移值应为

此时，阵列的空间相位差与阵内相位差将不再相等，两者之间的差值为

相位之间的差值导致在f0+Δf处，波束指向变为

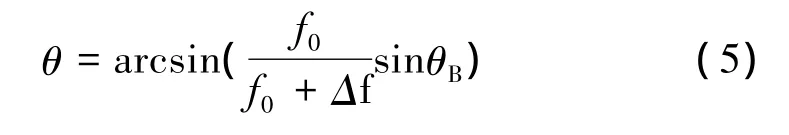
例如，移相器以中心频率8 GHz，波束指向45°的目标信号进行相位补偿，当频偏0.2 GHz时，仍进行相同的相位补偿将导致波束指向偏移到43.62°。图2即为中心频率为8 GHz，信号带宽400 MHz时，仅采用移相器进行波束扫描的结果。仿真中，阵列为128元均匀线阵，阵元间距为中心频点所对应波长的一半。

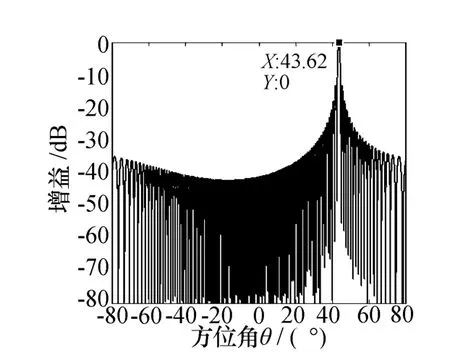
图2 仅使用移相器波束扫描图

以上的分析与仿真说明，信号频率变化引起的波束指向偏移随信号带宽与扫描角的增加而增加。由此可见，若要实现相控阵天线的大瞬时带宽，需要解决空间色散问题。

1.2 时间色散

最大允许的信号瞬时带宽除受波束指向偏移的限制之外，还受到阵列孔径渡越时间的影响。一维线阵的阵列孔径可表示为

式中:P为阵列首尾两端阵元的距离。假设有一来自θB方向的信号，到达两端天线的时间差为

式中:TA为孔径渡越时间，它反映阵列两端单元收到来自同一目标信号的时间差。假设信号带宽为B(B=2Δf)，那么该信号的脉冲宽度可表示为

通过图3可以很容易理解，当孔径渡越时间TA大于信号带宽的倒数T时，接收到的信号将无法直接合成。

图3 孔径渡越时间对瞬时带宽的影响

2 子阵级处理扩大瞬时带宽

通过以上的分析发现，仅仅在阵元级采用移相器不可能获得大的瞬时带宽。从理论上讲，在阵列每个单元采用实时延时线可以有效地实现任意大瞬时带宽的要求。在工程中，常采用六位数字移相器实现波束扫描，即数控移相器的分辨率为5.625°，转换为弧度制约为0.098 2 rad，在进行方向图运算时，相位权等同于指数函数ejφ。依此分辨率，则 φ为在［0，2π］内为0.098 2的整数倍，若将此分辨率转换成TTD的延时精度，分辨率约为

当中心频率为8 GHz时，分辨率约为1.95 ps。大孔径阵列往往需要总延时量至少为纳秒级的延时线，则TTD至少为10位数控延时线。如此高精度的实时延时线成本往往很高，并且，即使设备有皮秒级的延时误差，也会对波束指向产生很大影响。若使用分辨率低的延时线，量化误差将会导致波束的严重畸变。因此，在实际中多采用子阵划分的策略在子阵级使用实时延时线，阵元级使用移相器扩展阵列瞬时带宽。工程中多采用均匀子阵划分，因为子阵间规模相同可以增强通道间的一致性，减小通道间幅相误差影响，并且可以使阵列接收端设备种类数降低，实现低成本，同样有利于后期的阵列误差校正，提高可操作性。因此，本文阵列处理方式均采用子阵均匀划分方案。

下面，将从理论角度，分析采用子阵级TTD+阵元级PS实现宽带波束扫描的可行性。图4给出了子阵级处理的结构图。

图4 子阵级信号处理

假设一个M元线阵，均匀划分为N个子阵，每个子阵内 L个阵元，信号带宽为［f0-Δf，f0+Δf］，在不考虑量化误差并假设子阵级TTD已经补偿宽带信号时间色散影响的条件下，子阵级TTD的等效相移量为

式中:f=f0+Δf;n为子阵序号。阵元级移相器的相移量为

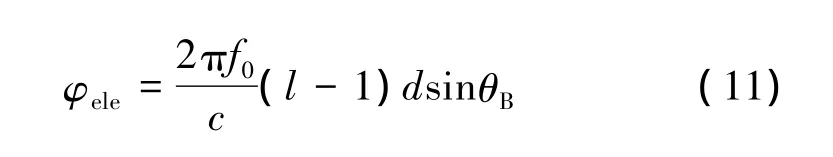
式中:l为子阵内的阵元序号。将每个子阵的相移量等效为阵元级的相移量后，每个阵元的总相移值为

在频率f处，若要实现无偏差的波束合成，每个阵元应得到的馈相值为

由式(12)、式(13)可得每个阵元的相位误差为

通过式(4)与式(14)对比可以发现，仅采用移相器的阵列中每个阵元的相位误差随阵元距参考单元距离的增加而线性增加;而采用子阵级TTD相当于将每个子阵的相位误差进行整体补偿，即阵元相位误差仅与子阵孔径有关。通过计算可以得到子阵级TTD处理后的阵列方向图为

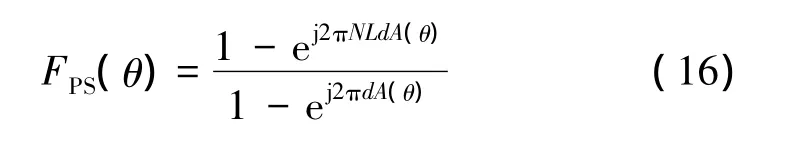
通过对比式(15)与式(16)也可以发现，子阵级TTD处理后的方向图由子阵方向图与子阵级阵列方向图两部分组成，而前一部分是导致波束指向偏移的主要原因。

综上所述，在子阵级使用TTD可以明显减少补偿相位与理论相位值之间的误差，改善宽带信号波束指向偏移的问题。下面将通过仿真对子阵级TTD+阵元级PS策略的性能进行分析。

仿真条件:128元线阵均匀划分为8个子阵，阵元间距d为信号中心频率f0对应波长的一半，中心频率为8 GHz，信号偏离中心频率Δf=0.2 GHz，仿真结果如图5所示。

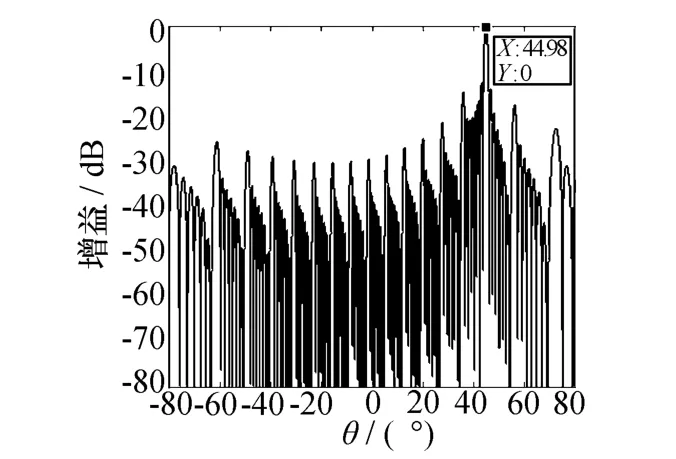
图5 子阵级TTD+阵元级PS处理阵列方向图

将图5与图2对比可以发现，在宽带信号中心频率为8 GHz，偏离中心频率0.2 GHz的条件下，子阵级TTD+阵元级PS处理方法的阵列波束指向为44.98°，因此，该方法可以有效抑制波束指向偏移问题。图5中高旁瓣是由于阵列均匀划分后，子阵间相位中心距离远大于半波长且呈周期性分布产生栅瓣所致。

前文已经说明，指向偏移是由于工作频率偏离中心频点时，阵元所得到的移相值与理想值不同导致的。下面通过仿真说明图4与图1两种阵列处理方法的相位补偿误差情况，仿真条件与图5仿真条件相同。

图6 相位补偿误差分析

图6a)中三条曲线分别表示没有经过“模2π”运算，在中心频点f0=8 GHz，接收信号f=f0+Δf=8.2 GHz条件下，阵元的理想相位补偿值、仅采用移相器的实际相位补偿值以及采用子阵级TTD+阵元级PS的实际相位补偿值，即为式(17)的仿真图，式中参量如前文所述;为方便观察，图6b)为第65～80号阵元局部放大的相位补偿，图6c)为经“模2π”处理后，第65～80号阵元局部放大的相位补偿图;图6d)为每个阵元相对理想相位补偿值的补偿误差图。

以上仿真图表示阵元级等效相移值与理想相移值的偏离程度，通过这组仿真可以发现，仅使用移相器的阵列相位误差呈线性增加，并且与理想相移值有较大误差。因此，波束指向偏移大;而子阵级TTD+阵元级PS的方法可以有效降低相位补偿误差。所以，波束指向偏移在此条件下仅为0.02°。从图6d)中也可以发现，仅采用PS不进行阵列划分相位补偿误差无周期性，而经过均匀划分后的子阵级TTD+阵元级PS方法的相位补偿误差呈周期性，这也说明了图5仿真中出现栅瓣的原因。

3 TTD分级使用扩展瞬时带宽

通过以上分析，可以发现子阵级TTD+阵元级PS的方法对改善瞬时带宽是有效的。但是，假设阵列孔径为P，阵元数为 M，阵元间距为 d，最大指向角为θmax，则需要的每个实时延时线总长度为

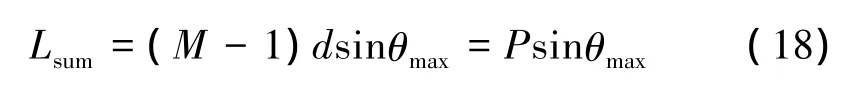
因此，延时线的长度及分辨率将使设备成本偏高。若减少此种延时线在阵列中的使用数量，将会大幅降低设备的成本。基于此，本文提出一种延时线的分级使用方法，阵列处理结构如图7所示。

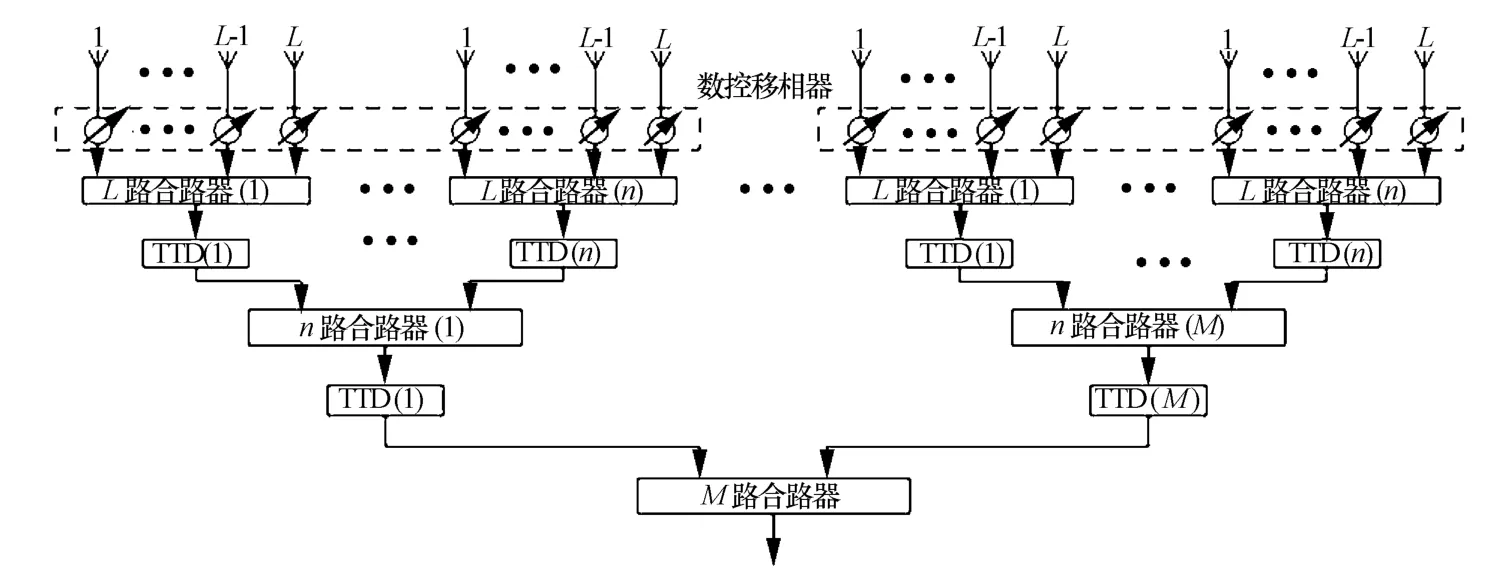
图7 两级TTD结构

在这种结构中，最外层子阵采用和前文一样的延时线，内层子阵仅需采用总长度为内层子阵孔径大小的延时线即可，大大降低了延时线的长度，节约了设备成本。下面，同样以128元均匀线阵为例，对采用此种策略进行方向图仿真。处理方法为先将全阵列划分为16个子阵，然后将16个子阵进一步划分为4个子阵。仿真结果如图8所示。

图8 TTD两级使用仿真图

图8a)为信号带宽400 MHz时的方向图，与图5对比可以发现，第一栅瓣电平降低了6.8 dB。图8b)为信号带宽 800 MHz，即 f0=8 GHz，f=f0+Δf=8.4 GHz条件下，两种子阵处理方法的性能对比。可以看出，运用两级TTD方法使第一栅瓣电平降低了7.6 dB，仔细对比可发现，单级TTD的指向为44.96°，而TTD两级使用的波束指向为44.98°，精度更高。若要满足第一旁瓣电平低于-15 dB要求下实现宽带信号接收，本文提出方法可实现的瞬时带宽是单级TTD方法的2倍。在实际中，两级TTD的延时量控制由子阵间的相对位置决定，阵元级移相器的波控码由子阵内阵元相对位置及在中心频点处两级TTD的量化误差同时决定。本文分级使用TTD策略可扩大信号瞬时带宽的实质是减小了每个子阵的孔径大小。

综上分析可得，分级使用TTD的策略在适当增加馈电复杂度的条件下，降低了成本并可实现更大的瞬时带宽。

4 结束语

本文首先从理论角度分析了相控阵天线瞬时带宽的限制因素;然后，通过公式计算得出采用子阵级TTD+阵元级PS方法扩展瞬时带宽的可行性;最后，提出了一种TTD分级使用的方法。仿真分析表明:该方法在适当增加馈电复杂度的代价下，降低了系统成本并可以实现更大的瞬时带宽。本文对宽带相控阵天线的工程设计具有一定的指导意义。

［1］Rodenbeck C T，Kim S G，Tu W H，et al.Ultra-wideband low-cost phased-array radars［J］.IEEE Transactions on Microwave Theory and Techniques，2005，53(12):3697-3703.

［2］Yajima M，Hasegawa T.Beam pointing error of wideband phased array antennas with reduced true-time-delay devices［C］//IEEE Global Telecommunications Conference.［S.l.］:IEEE Press，2005.

［3］Wang J，Cai D，Lei P.Aperture effect influence and analysis of stepped frequency wideband phased array radar［C］//2011 IEEE CIE International Conference on Radar.Chengdu:IEEE Press，2011.

［4］张 蕾，郭陈江，丁 君.子阵级应用延迟线对相控阵天线带宽改善的分析［J］.航空计算技术，2008，37(6):65-67.Zhang Lei，Guo Chenjiang，Ding Jun.Improving band width of the phased array antennas based on sub-array true time delayers［J］.Aeronautical Computer Technique，2008，37(6):65-67.

［5］朱瑞平，王朝阳.一种低栅瓣大瞬时带宽相控阵天线的设计方法［J］.电波科学学报，2008，23(4):745-748.Zhu Ruiping，Wang Chaoyang.Design method for wide band and low grating lobe phased array antennas［J］.Chinese Journal of Radio Science，2008，23(4):745-748.

［6］张光义.相控阵雷达瞬时带宽的几个问题［J］.现代雷达，1990，12(4):1-10.Zhang Guangyi.Several problems of the instantaneous bandwidth of phased array radar［J］.Modern Radar，1990，12(4):1-10.

［7］张金平，李建新，孙红兵.宽带相控阵天线实时延时器分级应用研究［J］.现代雷达，2010，32(7):75-78.Zhang Jinping，Li Jianxin，Sun Hongbing.A study on layered scheme of real-time delayers for the widebond phased array［J］.Modern Radar，2010，32(7):75-78.

［8］LaManna M.Performance study of an ultra wideband multifunction phased array［C］//2010 IEEE International Symposium on Phased Array Systems and Technology.Waltham，Massachusetts:IEEE Press，2010:498-503.

［9］高 铁，李建新，郭燕昌.相位量化对相控阵天线峰值副瓣电平影响的研究［J］.中国空间科学技术，1994，14(1):14-19.Gao Tie，Li Jianxin，Guo Yanchang.On effect of phase quantization upon peak sidelobe level in phased array atennas［J］.Chinese Space Science and Technology，1994，14(1):14-19.