无人机角跟踪系统抗干扰性能分析

盛怀洁，廖明飞

(合肥电子工程学院，安徽合肥230037)

0 引言

无人机角跟踪系统是无人机视距测控链路正常工作的关键系统，也是无人机测控系统抗干扰的薄弱环节。目前，往往将遥测遥控的抗干扰性能［1－5］等价为无人机测控系统的抗干扰性能，而忽略角跟踪这一关键环节。如何构建无人机角跟踪系统抗干扰性能指标，准确地衡量角跟踪系统的抗干扰性，是无人机系统电子防护急需研究和解决的问题之一。

通过分析无人机角跟踪系统的体制和干扰响应，构建了系统抗干扰性能指标，提出了系统抗干扰性能分析方法，在无人机角跟踪系统抗干扰性能分析方面做出了有益探索。

1 无人机角跟踪系统体制与干扰响应分析

根据角跟踪系统在角误差形成与提取方式上的不同，目前常用无人机角跟踪体制为相位干涉仪和单脉冲 2 种［6，7］。

相位干涉仪体制［7］自跟踪接收系统的工作过程是:利用分开一定距离的成对天线，接收飞行器的下行信号，通过处理提取2路信号的高频相位差，得到与目标偏离天线等信号轴的量值和方向有关的误差电压，再经转换后控制伺服，驱动天线始终自动对准目标。

单脉冲体制［7］自跟踪接收系统的工作过程是:利用波束部分重叠的成对波束或空间分立的两平行波束接收飞行器下行信号，通过提取和比较两波束形成的信号振幅关系或相位关系，得到与目标偏离天线等信号轴的量值和方向有关的误差电压，以此电压适当变换得到伺服系统的控制电压，控制伺服使天线自动对准目标。与相位干涉仪角跟踪系统相比，单通道的单脉冲系统在系统结构组成上相对简单，这也是单通道的单脉冲系统在当前无人机角跟踪系统中得到大量运用的重要原因。

无人机角跟踪系统的相位干涉仪体制和单脉冲体制均属于“同时波瓣”原理测角跟踪的范畴，2种体制的跟踪测角均是几乎同时接收两信号，通过比较而得出角误差，理论上获得角误差信息的时间可以很短。“同时波瓣”原理决定:干扰进入系统后，可以和跟踪信号一样，经天线接收后形成与干扰源方向有关的偏角信息，而角跟踪系统不具有识别此偏角信息的能力。因此，分析干扰对无人机角跟踪系统的影响时，不能仅仅将干扰的效果视为对跟踪误差提取过程信噪比的降低［8，9］。定性分析可知，利用了“同时波瓣”原理的无人机角跟踪系统，对干扰的响应可分为2种:

①干扰与跟踪信号同时进入角跟踪系统，在系统提取角误差前，干扰信号相对于天线指向的偏角信息没有畸变，经过跟踪接收机提取的误差电压同时包含跟踪信号和干扰信号的偏角信息，误差电压所对应的偏角为两者偏角信息与各自功率的加权合成，干扰使系统对合成信号方向形成稳定跟踪，干扰效果是使角跟踪系统的跟踪指向背离，此时的干扰可定义为对无人机角跟踪系统的诱偏干扰;

②干扰与跟踪信号同时进入系统，在系统提取角误差前，干扰信号相对于天线指向的偏角信息发生畸变，经过跟踪接收机提取的误差电压在均值上仅与跟踪信号偏角信息有关，方差与干信比有关，此时的输出误差电压控制伺服系统，将引起天线跟踪角度的抖动，干扰对无人机角跟踪系统的干扰效果是使角跟踪系统的跟踪精度下降，此时的干扰可定义为对无人机角跟踪系统的抖动干扰。

据上所述，认为干扰信号在角跟踪系统处理过程中能否保持其偏角信息是干扰响应类型的判定条件。当干扰信号经过角跟踪系统的处理保持了其偏角信息时，为诱偏干扰;反之，为抖动干扰。系统抗干扰性能指标的构建可以以干扰响应的分类为依据，建立适应性指标，以达到准确分析、全面衡量系统抗干扰性能的目的。

2 无人机角跟踪系统抗干扰性能构建

从对无人机角跟踪系统干扰响应的分析可知，诱偏干扰和抖动干扰这2种干扰响应在形成机理上存在差异，难以用1个或多个通用指标衡量其抗干扰性能。针对不同干扰响应，分别建立了内部噪声信噪比处理增益GN、诱偏干扰功率压制系数Ka、抖动干扰功率压制系数Kj和抖动干扰信噪比处理增益KG4个抗干扰性能指标，用于衡量无人机角跟踪系统固有抗干扰特性［10］以及系统在2种干扰响应类型下的抗干扰性能［11］。

2.1 内部噪声信噪比处理增益GN

如果将无人机角跟踪系统的内部噪声等效为其一中频输入端的一个噪声项，则系统鉴相器输入端的信噪比将与系统一中频输入端信噪比、系统结构组成和信号处理方法相关。两信噪比的比值可以一定程度地描述系统固有的抗干扰性能。

内部噪声信噪比处理增益GN的定义为:将无人机角跟踪系统的内部噪声等效到其一中频的输入端时，系统误差电压鉴相输入信噪比SNRo与一中频信噪比SNRi1的比值。其表达式为:

式中，SNRi1为角跟踪系统一中频信噪比;SNRo为系统误差电压鉴相器输入信噪比。

内部噪声信噪比处理增益GN的计算方法为:将系统的内部噪声等效至系统的一中频，作为总噪声项输入系统，推导建立等效到一中频的内部噪声与跟踪信号同时经过系统处理时，误差电压鉴相输入信噪比SNRo与一中频信噪比SNRi1和系统滤波带宽等参数的关系模型，直接将两信噪比相除即为系统的内部噪声信噪比处理增益GN。

内部噪声信噪比处理增益GN可以衡量不同角跟踪系统的潜在抗干扰性能。GN值越大，说明系统内部结构和信号处理技术对跟踪信号的筛选能力越好，对噪声的抑制性能越强，当外部干扰效果为形成大功率内部噪声时，系统更不易被该类型的干扰信号干扰，即要形成同样干扰效果，该类型干扰信号对此系统付出的干扰功率比对其他系统要大，此系统的抗干扰性能更好。

2.2 诱偏干扰功率压制系数Ka

当干扰信号经过角跟踪系统处理后，仍然保持其相对跟踪天线指向的偏角信息，跟踪接收机输出的误差电压所对应的偏角方向为干扰信号与跟踪信号两者功率、偏角加权合成的等效合成信号的偏角方向，此时所形成的干扰称为诱偏干扰。诱偏干扰形成时角跟踪系统将视干扰信号为另一个跟踪信号。

诱偏干扰功率压制系数［12］Ka的定义为:使跟踪天线指向与目标方向产生给定的偏差ε0时，角跟踪系统输入干扰功率Pj与信号功率Ps的比值。其表达式为:

式中，θs为干扰进入系统时跟踪天线指向与目标方向夹角;θj为干扰进入系统时跟踪天线指向与干扰方向夹角;θ0为指定的干扰进入方向与跟踪天线指向的夹角;θs'为角跟踪系统稳定时跟踪天线与目标方向夹角;ε0为给定的跟踪天线指向与目标方向夹角。

式(2)的初始条件为:跟踪天线指向与目标方向夹角θs=0，且与干扰源方向夹角为θj=θ0。

诱偏干扰功率压制系数Ka的计算方法为:建立干扰信号与跟踪信号同时进入无人机角跟踪系统时，系统输出误差电压 UΔ与系统输入干信比Pj/Ps、跟踪天线指向与干扰信号方向的夹角以及跟踪天线指向与跟踪信号方向的夹角的多维关系模型。令最终误差电压UΔ=0，得到天线最终指向与干信比Pj/Ps的二维关系，取跟踪天线最终指向与目标的偏角的绝对值等于给定的跟踪天线指向与目标方向夹角ε0，此时的系统输入干信比Pj/Ps即为系统对该干扰的诱偏干扰功率压制系数Ka。

诱偏干扰功率压制系数Ka可以衡量某一角跟踪系统对不同诱偏干扰源的抗干扰性能，Ka值越大，说明对该系统产生同样诱偏干扰效果所需的干扰功率越大，系统对该干扰的抗干扰能力越强;反之，系统对该干扰的抗干扰能力越弱。

同样，诱偏干扰功率压制系数Ka还可以衡量不同角跟踪系统的抗干扰性能。干扰信号相同的条件下，Ka值越大，说明跟踪信号功率相同时对该系统产生同样诱偏干扰效果所需的干扰功率越大，该系统的抗干扰能力越强;反之，该系统的抗干扰能力越弱。

2.3 抖动干扰功率压制系数Kj

当干扰信号经过角跟踪系统处理，其相对跟踪天线指向的偏角信息发生畸变，跟踪接收机输出的误差电压在一定范围波动，输出误差电压的均值对应跟踪信号相对跟踪天线指向，方差对应与系统输入干信比和干扰偏角有关，此时所形成的干扰称为抖动干扰。抖动干扰形成时角跟踪系统将视干扰信号为内部噪声。

抖动干扰功率压制系数［12］Kj的定义为:使角跟踪系统达到给定跟踪精度ξ0时，系统输入干扰功率Pj与信号功率Ps的比值。其表达式为:

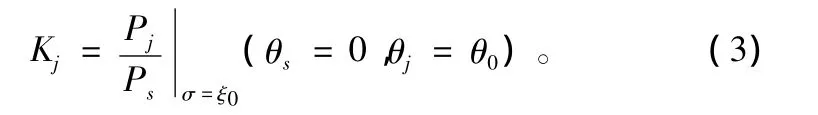
式中，θs为干扰进入系统时跟踪天线指向与目标方向夹角;θj为干扰进入系统时跟踪天线指向与干扰方向夹角;θ0为指定的干扰进入方向与跟踪天线指向夹角;σ为受干扰后角跟踪系统的跟踪精度;ξ0为给定的角跟踪系统跟踪精度。

式(3)的初始条件为:跟踪天线指向与目标方向夹角θs=0，且与干扰源方向夹角为θj=θ0。

抖动干扰功率压制系数Kj的计算方法为:建立干扰信号与跟踪信号同时进入无人机角跟踪系统时，系统最终跟踪精度σ与系统输入干信比Pj/Ps、系统的滤波特性和伺服系统参数等的关系模型。取跟踪精度σ达到给定值ξ0，此时的系统输入干信比Pj/Ps即为系统对该干扰的压制系数Kj。

抖动干扰功率压制系数Kj可以衡量某一角跟踪系统对不同抖动干扰源的抗干扰性能，Kj值越大，说明对该系统产生同样抖动干扰效果所需的干扰功率越大，系统对该干扰的抗干扰能力越强;反之，系统对该干扰的抗干扰能力越弱。

同样，抖动干扰功率压制系数Kj还可以衡量不同角跟踪系统的抗干扰性能。干扰信号相同的条件下，Kj值越大，说明跟踪信号功率相同时对该系统产生同样抖动干扰效果所需的干扰功率越大，该系统的抗干扰能力越强;反之，该系统的抗干扰能力越弱。

2.4 抖动干扰信噪比处理增益KG

此指标为抖动干扰功率压制系数Kj的简化。在伺服系统参数固定的条件下，当角跟踪系统误差电压鉴相器的输入信噪比小于内部噪声所对应的信噪比时，跟踪精度与误差电压鉴相器输入信噪比成正比关系。所以，只要推导系统输入信噪比(信干比)与误差电压鉴相器的鉴相输入信噪比的关系，即可描述此种抖动干扰效果的系统抗干扰性能。

抖动干扰信噪比处理增益KG的定义为:无人机角跟踪系统误差电压鉴相输入信噪比SNRo与系统输入信噪比SNRi的比值:

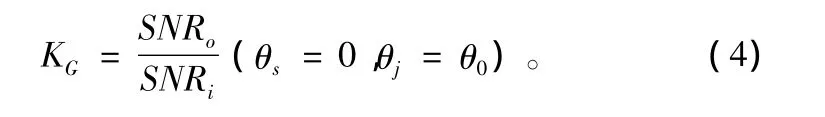
式中，θs为干扰进入系统时跟踪天线指向与目标方向夹角;θj为干扰进入系统时跟踪天线指向与干扰方向夹角;θ0为指定的干扰进入方向与跟踪天线指向夹角;SNRi为角跟踪系统输入信噪比(信干比);SNRo为系统误差电压鉴相器输入信噪比。

式(4)的初始条件为:跟踪天线指向与目标方向夹角θs=0，且与干扰源方向夹角为θj=θ0。

抖动干扰信噪比处理增益KG的计算方法为:建立干扰信号与跟踪信号同时进入系统时的误差电压鉴相输入信噪比SNRo与系统输入信噪比SNRi和系统滤波带宽等参数的关系模型，直接将两信噪比相除即为系统对该干扰的抖动干扰信噪比处理增益KG。

抖动干扰信噪比处理增益KG可以衡量某一角跟踪系统对不同抖动干扰源的抗干扰性能，KG值越大，说明对该系统产生同样抖动干扰效果所需的干扰功率越大，系统对该干扰的抗干扰能力越强;反之，系统对该干扰的抗干扰能力越弱。

同样，抖动干扰信噪比处理增益KG还可以衡量不同角跟踪系统的抗干扰性能。在干扰信号相同的条件下，KG值越大，说明跟踪信号功率相同时对该系统产生同样抖动干扰效果所需的干扰功率越大，该系统的抗干扰能力越强;反之，该系统的抗干扰能力越弱。因为此指标的建立没有将伺服系统包括其中，则此衡量的前提条件为各角跟踪系统的伺服系统性能相同。

上述指标的建立，为无人机角跟踪系统抗干扰性能的衡量提供了量化标准。

3 无人机角跟踪系统抗干扰性能分析方法

分析无人机角跟踪系统的抗干扰性能，首先构建角跟踪系统模型。不同体制下不同跟踪信号所对应的角跟踪系统模型包括:相位干涉仪窄带信号角跟踪系统模型、相位干涉仪宽带信号角跟踪系统模型以及单脉冲窄带信号角跟踪系统模型、单脉冲宽带信号角跟踪系统模型和单脉冲扩频信号角跟踪系统模型。对每一个系统，遵行下面的分析流程，如图1所示。

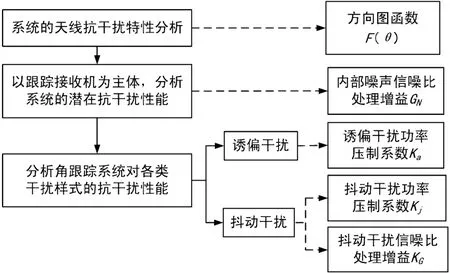
图1 无人机角跟踪系统抗干扰性能分析流程

天线抗干扰特性。主要分析跟踪天线的空域特性和频率特性，说明装配该天线的无人机角跟踪系统在天线接收部分对干扰所具备的抗干扰性能。用天线的方向图函数F(θ)定量表示系统天线的抗干扰性能。天线抗干扰特性的分析，也是分析各类干扰进入角跟踪系统时系统抗干扰性能的重要组成部分。

潜在抗干扰性能。系统对内部噪声的处理增益，体现系统潜在的抗干扰性能。系统对内部噪声的处理增益越高，则系统的跟踪接收灵敏度越高，系统潜在的抗干扰性能也越强。无人机角跟踪系统的内部噪声信噪比处理增益GN，是独立于各类干扰形式的重要的抗干扰性能组成部分。将内部噪声信噪比处理增益的指标值定义为系统的抗内部噪声性能。当干扰对无人机角跟踪系统的干扰效果为抖动干扰时，系统对干扰的抗干扰性能分析可以直接利用系统对内部噪声信噪比处理增益的结论。

对各类干扰信号的抗干扰性能。选择噪声调频干扰和噪声调幅干扰为典型的干扰样式，针对各个角跟踪系统，理论推导系统对干扰信号和跟踪信号的处理过程，确定具体干扰对系统的干扰效果——诱偏干扰和抖动干扰。然后根据分析得出的2类干扰效果，分别选取对应的抗干扰性能指标。对于诱偏干扰，选取式(2)所确定的诱偏干扰功率压制系数Ka;对于抖动干扰，选取式(3)所确定的抖动干扰功率压制系数Kj。当系统的伺服参数系统条件下或者当衡量同一角跟踪系统的抗干扰性能时，也可直接选取式(4)所确定的抖动干扰信噪比处理增益KG。通过指标的计算，最终定量分析无人机角跟踪系统的抗干扰性能，并将系统对噪声调频干扰和噪声调幅干扰的抗干扰性能拓展为系统抗宽带干扰和抗窄带干扰的性能。

通过以上步骤，得到系统的天线抗干扰特性、抗内部噪声性能、抗宽带干扰性能和抗窄带干扰性能，就可以比较完整地描述无人机角跟踪系统所具有的抗干扰性能。

4 结束语

在分析无人机角跟踪系统的体制以及系统对干扰的干扰响应基础上，构建了用于定量衡量无人机角跟踪系统固有抗干扰性能、特定干扰样式下抗干扰性能的4项抗干扰性能指标:内部噪声信噪比处理增益、诱偏干扰功率压制系数、抖动干扰功率压制系数和抖动干扰信噪比处理增益，并提出了一种分析无人机角跟踪系统抗干扰性能的方法，对无人机测控系统抗干扰性能的分析具有一定的价值。将指标进行综合分析以研究系统整体抗干扰性能则是继续讨论和研究的问题。

［1］ 胡 军，都基焱，刘文清．多无人机控制与定位系统的研究［J］．航空科学技术，2004(3):29－32．

［2］ 张 旭，吴 潜．扩频测控系统的抗干扰能力分析［J］．电讯技术，2011，51(5):24 －27．

［3］ 马传焱．无人机测控系统抗干扰技术与应用分析［J］．飞航导弹，2006(11):9－11．

［4］ 祁栋升，陈自力，白勇博，等．无人机数据链中Turbo码研究与 FPGA 实现［J］．无线电工程，2010，40(12):51－57．

［5］ 丁 丹，刘茂国．一种高效抗干扰无人机测控链路的实现［J］．电讯技术，2009，49(6):41－44．

［6］ 祝小平．无人机设计手册(下册)［M］．北京:国防工业出版社，2007:531－537．

［7］ 韩敬杰．无人飞行器跟踪测角体制研究［J］．无线电工程，2006，36(4):35 －36．

［8］ 张建伟，黄树彩，韩朝超，等．压制性干扰对反导导弹末制导精度的影响［J］．现代防御技术，2010，38(3):35－38．

［9］ 王冰洁，钱建军，赵 彤，等．混沌激光雷达抗干扰性能分析［J］．中国激光，2011，38(5):1 －6．

［10］周新刚，赵惠昌，张淑宁，等．典型近炸引信固有抗干扰性能测度理论和仿真［J］．系统仿真学报，2010，22(6):1 454－1 456．

［11］孙凤荣，冷东方，崔永久．搜索雷达抗有源噪声干扰效果定量评估方法［J］．航天电子对抗，2000(3):20 －23．

［12］罗景青．雷达对抗原理［M］．北京:解放军出版社，2003:284－292．