基于Logistic映射与LWT的音频隐写算法

赵哲鸿，高 勇

(四川大学电子信息学院，四川成都610065)

0 引言

近年来，由于互联网和数字媒体的广泛使用，用户的私有信息面临着很大的被泄露的危险。因此，如何增加信息在传输过程中的安全性成为了目前信息安全领域的一大难题。隐写术通过隐藏通信过程的存在性来保证通信的安全，它有3个性能指标，按照重要性排序依次是透明性、容量和鲁棒性。

隐写术主要以图像［1］、音频和文本等媒体为隐藏载体，本文以音频为研究对象。音频隐写算法主要指利用人耳听觉的掩蔽效应，将秘密信息隐藏到普通的音频数据流以达到隐蔽通信的目的的一种算法。音频隐写算法有很多种，其中具有代表性的算法有:最不重要位算法［2］、相位编码算法［3，4］、回声隐藏算法［4－6］、扩频隐藏算法［7］、基于离散傅里叶变换(DFT)隐写［8］、基于离散余弦变换(DCT)隐写［9］和基于离散小波变换(DWT)隐写［10－13］等。

通过对当前主流音频隐写算法的分析可以发现:传统的LSB算法虽然容量大，但是鲁棒性与透明性较差;相位编码算法与回声隐藏算法虽然鲁棒性和透明性有所提高，但是隐藏容量又偏小;扩频隐藏算法鲁棒性较好，但是不能兼顾透明与容量。文献［10］将秘密信息在小波域内进行嵌入，与传统的LSB方法相比，在相同容量的情况下提高了透明性，但是由于小波变换的系数是浮点数，在缩放过程中会导致误差的产生，因此恢复出来的秘密信息含有一定的噪音，影响舒适性。针对这个问题，Sajad等人在文献［11］中使用了小波提升的办法，使得小波变换实现了从整数到整数的变换，恢复的秘密语音的音质有了很大改善。该方法中被替换掉的载体小波系数的二进制比特的位数是动态变化的。由于此替换操作将导致含密载体小波系数值的改变，因此在恢复秘密语音的时候不能准确确定每个载体小波系数中被替换掉的比特位数。另外，该算法没有在前端对秘密语音进行置乱处理。而文献［12］利用了语音信号的小波系数在经过排序之后与载体音频信号的小波系数具有同样的形状这一特性，大大提高了含密载体的透明性。但是该方法引入了与秘密语音相同点数的秘钥，密钥长度过长，且该密钥是1～秘密信息长度的自然数，一旦秘钥遭到攻击将导致密钥值发生改变，从而使得秘密语音的小波系数的排序发生变化，不能正确恢复出秘密语音。

因此，针对以上出现的对秘密语音没有处理或处理不充分的问题，采用基于Logistic映射［14－16］的置乱方法对秘密语音进行预处理，具体做法如下:对秘密语音的每一个小波系数的二进制比特分别用同一个Logistic序列进行置乱，因为生成Logistic序列的时间与序列的长度成正比关系，而传统的扰乱方法需要生成与秘密语音相同长度的序列，而此方法生成的Logistic序列长度为固定的16位，并且与秘密语音的长度无关，这就相当于间接解决了序列长度过长导致的扰乱速度慢的问题。

1 音频隐写算法

1.1 整数小波提升变换

由于传统的小波变换是在傅里叶分析的基础上发展而来，因此在一定程度上受到傅里叶分析的限制。针对传统的小波变换存在的问题，在文献［13］中，Sweldens提出了一种不依赖于傅里叶变换的新的小波构造的方法——提升小波变换法，具有如下优点:① 能够实现快速运算;② 可节省存储单元;③逆小波变换的实现简单、快速且直接;④ 可以实现信号从整数到整数的变换。本文采用小波提升算法主要是利用了第④个优点。

提升小波变换的3个步骤如下:

①分解。将输入信号si分解成2个不相交的子集，最简单的办法是将si根据奇偶性分成2组，分解过程表示为 F(si)=(si－1，di－1)。其中 si－1表示偶数子序列，di－1表示奇数子序列。

②预测。在基于原始数据相关性的基础上，用偶数子序列si－1的预测值P(si－1)值去预测奇数子序列di－1，P为预测算子。然后用更小的子集si－1和奇数子序列di－1代替原始信号集si。经过n步重复分解和预测过程之后，原始信号集si可以用{sn，dn，．．．，s1，d1}表示。

③更新。更新的目的是使原信号的某些全局特性在它的子集si－1之中能够继续保持。为了保持原信号的全局特性就必须构造一个更新算子U，它的定义如下:

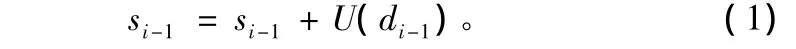
以上3个步骤完成了一次正向提升，即传统小波变换的一层分解。重构的过程与正向提升相反，首先逆更新恢复出偶数序列，之后由偶数序列逆预测出奇数序列，最后将奇数序列与偶数序列重构出原始信号。

1.2 Logistic映射

Logistic序列具有构造简单、对初始值和控制参数敏感的特点，并且它可以通过初始值精确重构。经过Logistic序列映射之后的信号具有混沌特性，很难预测，其表达式为:

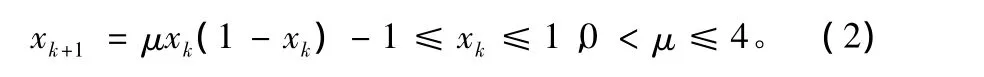
式中，μ为控制参数。由上述公式产生的序列完全依赖于初始值x0以及控制参数μ，即使初始值发生很小的扰动，序列的结果也将完全不同，因此，可将初始值和控制参数看作整个混沌序列的一把密钥。通常，用Lyapunov指数来判别一个系统是否具有混沌特性，当系统的Lyapunov指数为正时，系统才呈现出混沌状态。文献［14］中指出，只有当控制参数μ∈［3.75，4)之间时，Logistic序列才呈现出混沌状态。在本文中，置乱采用的Logistic序列初始值为x0=0.81，μ =3.96。

1.3 秘密语音的嵌入

为了嵌入秘密语音，对秘密语音和载体语音都进行整数小波提升变换。在做整数小波提升变换之前，先把秘密语音和载体语音采样点的值都变成整数，之后利用提升小波变换构造出Harr小波的提升小波基，并利用这个提升小波基对载体语音和秘密语音进行整数小波提升运算，这样得出的载体和秘密语音小波系数就是整数。假设秘密语音为S、长度为N，表示为:S={s(n)，1≤n≤N}。首先，对S用Harr小波基进行一次小波提升变换，将得到的小波系数转化为二进制数据串，表示为:

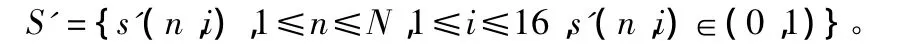
然后对每个s'(n，i)用相同的Logistic序列进行置乱。假设载体语音为H、长度为N1，用H={h(k)，1≤k≤N1}表示，对载体语音用与秘密语音一样的小波基函数进行提升变换，并将得到的整数小波系数转化为二进制数，表示为:

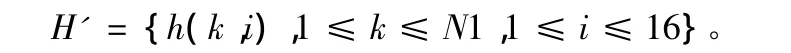
综合考虑隐藏容量和算法鲁棒性等因素，将S'中的比特对应地替换H'比特的第9～12位，得到新的载体小波系数H″。将H″做逆向小波提升变换得到含密载体语音H‴。音频隐写算法的秘密语音嵌入原理如图1所示。

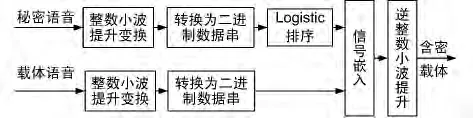
图1 秘密语音的嵌入原理

1.4 秘密语音的提取

秘密语音的提取过程是隐藏过程的逆过程。首先，将Haar小波基函数进行提升，之后再用提升之后的小波对含密载体语音进行小波提升分解，对得到的小波系数进行二进制转换，再依次取出每个二进制数的9～12比特位，将它们整合到一起构成扰乱之后的秘密语音小波系数，最后再对它们用Logistic序列解扰乱，得到正确排序的秘密语音小波系数，将这些系数进行逆小波提升变换，得到恢复出的秘密语音。

2 仿真及实验分析

实验采用的秘密语音长度为5 s，采样频率为8 kHz，分辨率为16 bit，载体语音长度为20 s，采样频率为8 kHz，分辨率为16 bit。秘密语音和载体语音的小波提升的小波基均选用Harr小波，置乱用到的Logistic序列的初始值x0=0.81，μ =3．96。

2.1 透明性分析

原始秘密语音、原始载体语音、恢复出的秘密语音和含密载体语音波形如图2所示。

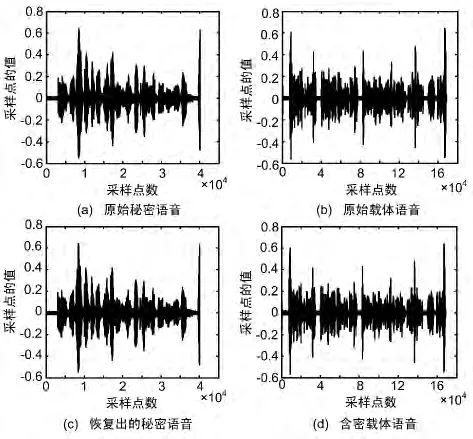
图2 透明性分析

通过观察图形可以看出，藏入了秘密语音的载体与原始载体几乎没有差别，说明了该算法的透明性比较好，并且由该算法恢复出的秘密语音与原始秘密语音也有很大的相似度。

图2是通过图形直观地分析算法的透明性，在客观上，用信噪比(SNR)来衡量嵌入秘密语音后载体的失真，定义为:

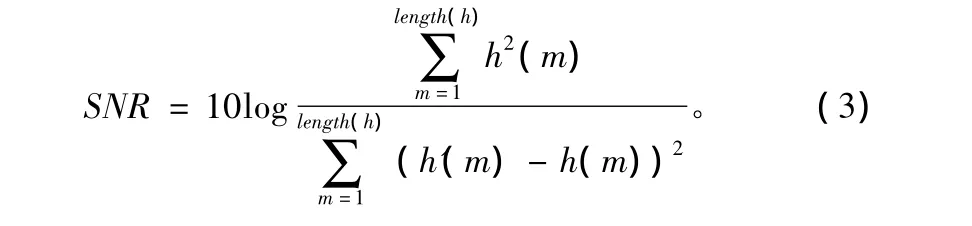
式中，h(m)表示原始载体语音;h'(m)表示含有秘密语音的载体语音。用归一化相关系(NC)来衡量恢复出的秘密语音的失真，定义为:

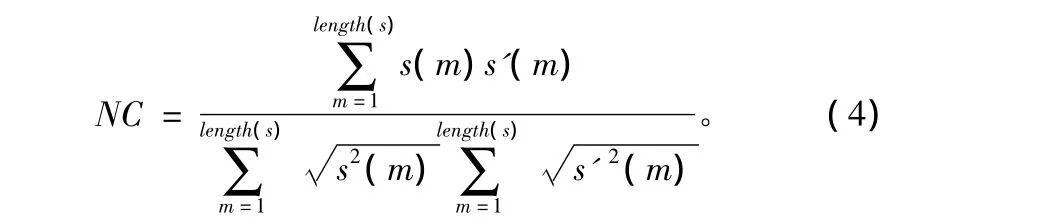
式中，s(m)表示原始的秘密语音;s'(m)表示恢复出的秘密语音。SNR与NC的值越大，说明算法的透明性越好。由该算法计算出的载体信息的SNR为23.803 5 dB，密语音的NC值为0.996 8。这些数据从客观上说明该算法的透明性好，而且恢复出的秘密语音几乎与原始的秘密语音一模一样，语音的舒适度较好。

2.2 容量分析与网络传输结果

将含密载体音频信号经过QQ传输之后的载体以及恢复出的秘密语音如图3所示。

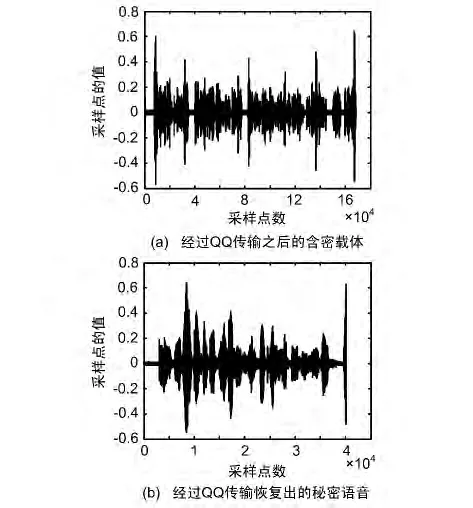
图3 网络传输性能分析

本文算法将每个载体小波系数与秘密语音小波系数均转化为16 bit，且每个秘密语音的小波系数只替换掉载体小波的9～12这4位，说明该算法的容量最高可达载体容量的25%，比文献［10］中的算法高出5%。

求出将含密载体语音信号经过QQ传输之后载体的SNR以及恢复出的秘密语音的NC的值，并将它们与不经过QQ传输的情况进行对比，得出的结果如表1所示。

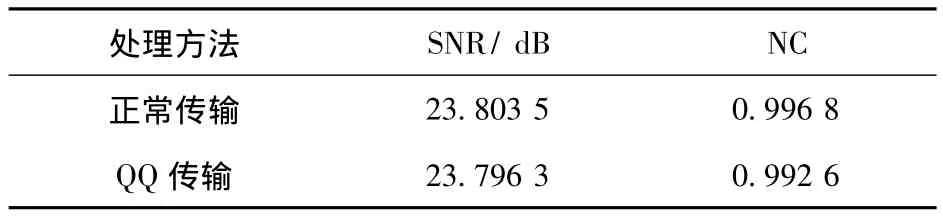
表1 网络传输性能指标

通过以上图形及数据可以看出，经过QQ网络传输之后，含密载体的SNR与秘密语音的NC基本上没有发生变化，说明该算法在经过网络传输之后，也能够正确地提取出原始的秘密语音信号。

3 结束语

本文提出的Logistic置乱与小波提升的高层LSB音频隐写算法，容量比文献［10］提高了5%，另外在前端的置乱加大了破解秘密语音的难度，与传统的LSB算法相比，鲁棒性更好。实验证明该算法网络信道中传输含密载体信号之后，能够正确提取出秘密语音，且提取秘密信息时不需要原始载体，具有一定的实用价值。

［1］ 周福成，杨任尔，何加铭．一种基于像素差和菱形编码的图像隐写方法［J］．无线电通信技术，2013，39(4):76 －80，88．

［2］ MOHAMMAD P，AHMAD D．LSB-based Audio Steganography Method Based on Lifting Wavelet Transform［C］∥2007 IEEE International Symposium on Signal Processing and Information Technology，2007:600-603．

［3］ ZENG Wei，AI Hao-jun，HU Rui-min．A Novel Steganalysis Algorithm of Phase Coding in Audio Signal［C］∥Sixth International Conference on Advanced Language Processing and Web Information Technology，2005:261－264．

［4］ BENDER W，GRUH D，MORIMOTO N，et al．Techniques for Data Hiding［J］．IBM System，1996，35(3):313 －336．

［5］ DANIEL G，ANTHONY L，WALTER B．Echo Hiding［C］∥Proc．Info．Hiding Workshop，1996:295 －315．

［6］ VALERY K．The Use of Wet Paper Codes with Audio Watermarking Based on Echo Hiding［C］∥ Proceedings of the Federated Conference on Computer Science and Information Systems，2012:727 －732．

［7］ 同 鸣，郝重阳，刘晓军．基于听觉掩蔽效应特性的扩频信息隐藏方法［J］．计算机工程，2006，32(10):137－139．

［8］ SIWAR R，DRISS G．．Speech Steganography Using Wavelet and Fourier Transform［J］．EURASIP Journal on Audio，Speech，and Music Processing，2012，1(20):1 －14．

［9］ MAZDAK Z．Efficient Embedding for Audio Steganography［C］∥Models and Methods in Applied Sciences，2012:195－199．

［10］ CVEJIC N，SEPPANEN T．A Wavelet Domain Insertion Algorithm for High Capacity Audio Steganography［C］∥Proc．of 10th IEEE Digital Signal Processing Workshop and 2nd Signal Processing Education Workshop，2002:53－55．

［11］ SHIRALI-SHAHREZA，MANZURI-SHALMANIM T．High Capacity Error Free Wavelet Domain Speech Steganography［C］∥ IEEE International Conference on A-coustics，Speech，and Signal Processing，2008:1 729 －1 732．

［12］ BALLESTERO L Dora M，MORENO A Juan M．Highly Transparent Steganography Model of Speech Using Efficient Wavelet Masking［J］．Expert System with Application，2012(39):9 141 －9 149．

［13］ SWELDDENS W．The Lifting Scheme:A Construction of Second Generation Wavelets［J］．SIAM Journal on Mathematic Analysis，1998，29(2):511 －546．

［14］王也隽．信息隐藏技术及其军事应用［M］．北京:国防工业出版社，2011．

［15］李涛护，高保生．基于Logistic-map的长周期混沌序列发生器［J］．无线电工程，2014，44(2):77 －80．

［16］孙文军，芮国胜，张 嵩，等．微弱信号混沌检测方法的抗噪性能研究［J］．无线电通信技术，2012，38(1):59－62．