中国农业生产资料价格的波动特征研究——基于GED分布下EGARCH

中国农业生产资料价格的波动特征研究——基于GED分布下EGARCH－M模型

2014-01-01史常亮朱俊峰

统计与信息论坛 2014年11期

史常亮，朱俊峰，栾江

（1．中国农业大学经济管理学院，北京100083；2．中共天津市委党校经济学教研部，天津300384）

一、引言

根据市场经济理论，农业生产资料（简称“农资”）价格波动直接影响着农资市场供给与需求结构，并且对农资经营者的动机与预期产生影响。特别是随着中国农资供给体制市场化改革进程的推进，以及政府对化肥等主要农资经营限制的放开，市场经营主体增多，众多农资生产经营者，特别是中小农资生产经营者已经将其视为谋取生计的主要途径。政府在对农资经营者进行扶持、培育的过程中，也需要价格机制作为引导工具。在这种背景下，对农资价格波动特征进行探究，既能够为农资生产经营者合理安排生产提供参考，也为深化农资市场供给、流通体制改革，完善农资市场功能提供理论依据。

相较于农产品价格波动，学者们对农资价格波动问题的关注较少，但也初步形成了一些研究成果。如铺甫宁等通过对中国农资市场化改革历程的回顾，认为随着农资市场化改革的不断深化，农资价格由市场形成的范围正不断扩大［1］。王侃等计算了尿素、磷酸二氨和氯化钾等主要化肥品种的需求价格弹性，发现化肥需求量对价格变化的反应不是很敏感，比较缺乏弹性［2］。王新志分析了始于2003年底的新一轮农资价格上涨特点，发现具有涨幅大、持续时间长的特征［3］。金赛美、韩艳旗等讨论了农资销售的季节集中性对农资价格的影响，认为季节性导致大多数农资产品的需求缺乏弹性，致使价格有一定程度的升高，发现春耕的农资价格要比一年中其它时间更高［4－5］。

在研究价格波动方面，能够反映具有“某一阶段波动平稳、某些阶段波动剧烈”特征的自回归条件异方差（ARCH）类模型，无论是从理论研究的深度还是从实证运用的广泛性来说都是独一无二的。国内已有许多文献运用该类模型，对农产品价格波动的一些基本特征，如集聚性、非对称性、波动的持久性等进行了检验［6－7］。针对中国农资市场的运行中格波动的特征，有学者展开了实证研究，但尚未给出比较明确和统一的推断。如黄文彪等运用ARCH族模型对农资价格波动特征进行分析，发现农资价格波动存在明显的聚集性和长期记忆性，但不存在高风险高回报和非对称效应［8］。马凯等的研究却表明，中国农资价格波动具有显著的非对称性［9］。张文雄等对化肥的分析也表明，非对称效应在农资类产品价格波动中是存在的［10］。

总体而言，目前关于中国农资价格波动的定量研究还不充分，还存在如下问题：一是大部分研究仍停留在对农资涨价的短期现象与成因的一般性描述层面，缺乏对其长期变动规律及波动特征的深层次探讨；二是应用ARCH类模型对农资价格波动的分析主要集中在波动聚集性上，对其波动的杠杆效应分析较为缺乏；三是在构建ARCH类模型时，都忽略了对时间序列扰动项分布特征的讨论，造成拟合效果欠佳，不能得出令人信服的结论。鉴于此，本文试图将GAECH－M模型和EGARCH模型相结合，形成EGARCH－M模型，分析中国农资价格的波动聚集性和杠杆效应，探讨在正态分布、T分布以及GED分布三种情况下中国农资价格波动的最优分布形式，以提高模型的拟合效果。

二、研究方法

基于数据的可得性，本文利用1994年1月至2014年3月农业生产资料价格总指数的月度数据进行研究，数据来自各期《中国经济景气月报》。为了反映农资价格的波动情况以及计算本月价格相对于上月的变化率，需要农资价格定基指数的月度时序数据，但根据官方公开统计资料仅能获取2006年以后的月度环比数据，而此前只有月度同比数据。为此，本文利用2006年以后月度环比数据和之前的同比数据，以1994年1月为基期得到定基月度农资价格指数。月度时间序列数据能够较好地反映波动规律，但受农业生产周期的影响，农资月度价格指数序列不可避免地包含了季节性因素，必须剔除季节因素影响。本文将采用X12－ARIMA模型对原始序列进行季节调整。对剥离了季节因素的价格数据，采用HP滤波分析其周期性特征，再采用EGARCH－M模型分析其波动聚集性和杠杆效应。

（一）X12－ARIMA季节调整模型

经济时间序列的变化通常受到自身的趋势、周期、季节及不规则成分的影响。设Yt表示一个无奇异值的月度时间序列，季节调整就是从Yt中去除季节成分St和不规则成分It，从而显示出能够真实地反映Yt运动的客观规律的趋势循环分量TCt的过程。目前，国际上通用的季节调整的方法主要有X11－ARIMA、X12－ARIMA和 TRAMO／SEATS这三种。其中，X12－ARIMA作为X11－ARIMA的提高版，囊括了后者的所有特性，同时还改进了在建模和诊断能力方面的缺陷，而且与TRAMO／SEATS相比，X12－ARIMA在调整效果控制、异常值处理、季节模式识别等方面也具有更优良的特性。该模型的基本形式为：

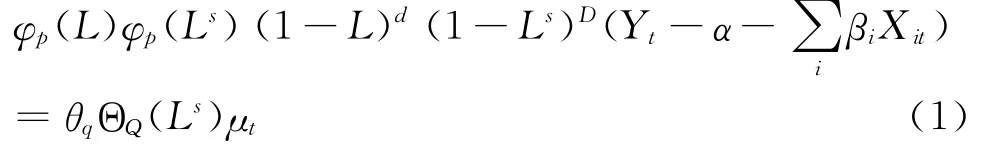
式中L是滞后算子，s为季节周期的长度（月度数据s＝12，季度数据s＝4），d、D分别表示非季节性差分阶数、季节性差分阶数，φp（L）、θq（L）分别表示非积极性p阶自回归算子、q阶移动平均算子，φp（Ls）、ΘQ（Ls）分别表示季节性p阶自回归算子、Q阶移动平均算子，μt为白噪声过程，Yt是原始时间序列，Xit是回归变量。除了能够有效处理变量的季节性外，X12－ARIMA还提供了3种方法来检验时间序列的季节性，包括季节稳定性F检验与Kruskal–Wallis卡方检验及移动季节性F检验。

（二）HP滤波方法

经X12－ARIMA方法季节调整后的趋势成分和周期成分是叠加在一起的，为得到研究价格波动周期所需要的周期成分，就需要去除趋势成分。HP滤波方法是消除时间序列中趋势成分被广泛使用的一种方法。设TCt是包含趋势成分和周期成分的经济时间序列，Tt是趋势成分，Ct是周期成分，则计算HP滤波就是从序列TCt中将趋势成分Tt分离出来，从而得到对应的周期成分Ct。一般地，Tt常被定义为下面最小化问题的解：

式中参数λ是对趋势成分Tt波动的正惩罚因子，需事先给定，按一般经验，月度数据的λ取值为14 400。

（三）EGARCH－M 模型

实证研究中，采用的高频率时间序列数据通常存在条件异方差问题，可能使回归结果难以评价。

由Engle提出的自回归条件异方差（ARCH）模型因为具有较好的时变方差和处理厚尾的能力，使得解决时间序列中的“异方差”成为可能，被广泛应用于各种经济类时间序列数据的分析中［11］。ARCH模型有两个方程构成：

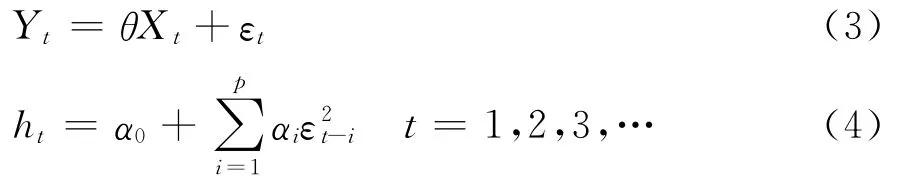
式（3）为均值方程，Yt是被解释变量；Xt是解释变量，可以是被解释变量的滞后项，也可以是其他外生变量；θ为待估参数向量；εt为误差项。式（4）为方差方程，ht表示εt的条件方差，包括常数项α0和ARCH（p）项（p为滞后阶数）。为确保条件方差ht＞0，要求α0＞0，αi＞0（i＝1，2，…，p）。

当ARCH模型中存在高阶ARCH效应时，为解决需要较多参数来充分描述波动过程的缺陷，可以采用广义自回归条件异方差（GARCH）模型［12］。该表达式是在式（4）中加入条件方差自身的滞后项：

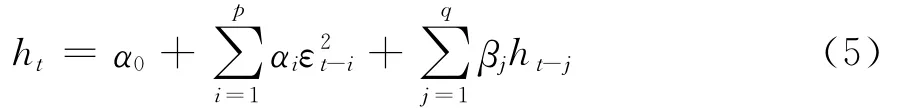
式（5）中，为 GARCH（q）项（q为滞后阶数），如果ARCH或者GARCH项高度显著，说明价格收益率具有显著的波动聚集性。为保证ht＞0，要求系数αi≥0和βj≥0（j＝1，2，…，q），但这只是保证模型有意义的充分条件而非必要条件。

在市场上，人们对价格涨跌的预期风险往往会影响未来的价格走势。为了度量这种价格预期风险对收益率的影响，可在ARCH模型的条件均值方程式（4）中引入条件方差项，得到GARCH－M模型：

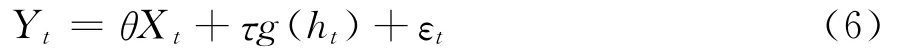
式（6）中，g（ht）是条件方差ht的单调函数，通常采用三种形式；参数τ是条件方差的倍数，是可观测到的预期风险波动对Yt的影响程度，它代表了风险和收益之间的一种权衡。如果τ显著为正，就意味着市场参与者会因为风险增加而要求更高的收益，即市场存在“高风险高回报”的风险报酬特征。

尽管GARCH模型对经济时间序列的厚尾和波动集聚现象描述比较成功，但是它却不能很好地反映数据中的非对称效应信息。为克服此弱点，Nelson提出了指数GARCH，即EGARCH模型［13］。与 TGARCH 及 PGARCH 模型相比，EGARCH无需施加对参数符号的任何限制，求解过程更为简单灵活，而且以条件方差的对数形式确保ht取正值，使模型更加稳定。EGARCH（p，q）模型的方差方程表示为：

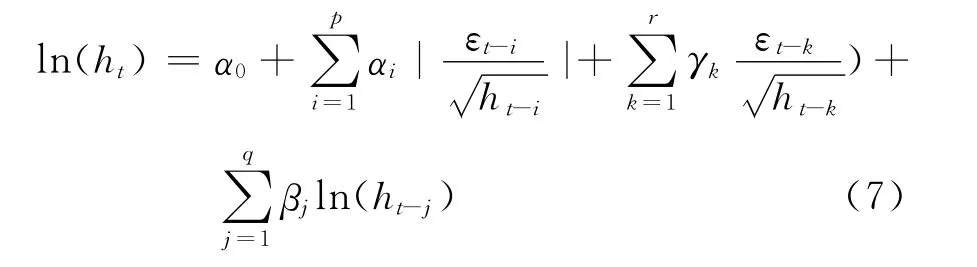
式（7）中，β的大小反映了波动的程度，β越接近于1，波动的持续性和聚集性就越强，这个系数等同于GARCH模型中的除了常数项之外的拟合系数之和。非对称性由γ来反映，若γ显著不为0，表示市场信息冲击对价格波动的影响存在着非对称性；当γ＞0时，表示正向冲击（价格上涨）对价格波动的影响大于负向冲击（价格下跌）的影响；当γ＜0时，表示负向冲击对价格波动的影响大于正向冲击的影响，此时也称作杠杆效应。

三、实证分析

（一）农资价格波动的季节性特征

由于农资价格随时间有递增趋势，使用X12－ARIMA中的乘法模型进行季节调整。季节性检验结果如表1所示：结果表明，农资价格存在稳定季节性、移动季节性和可识别季节性，也就是农资价格季节性波动显著，其波动不仅随月变化，还随年变化。

表1 农资价格季节性检验结果表

图1表明农资价格季节变化模式为：季节因素使农资价格在每年的1—4月份上涨0．3至0．7个百分点，8—9月份分别上涨0．1和0．2个百分点，11—12月份下跌1个百分点，其它月份比较稳定。这与农作物生产的基本规律是一致的：入春以来的1—4月份，是春耕春播的大忙季节，化肥、种子、农药、农膜等重要的农业生产资料进入销售旺季，相应的农资价格也达到全年的最高点；进入5月份以后，春耕用肥高峰期基本结束，各种农资价格涨幅也随之“止涨下跌”；8—9月份是夏秋季农资消费时节，也是传统的用肥旺季，农资价格呈现趋稳回升走势；年末（10—12月份）进入农闲时节和农资销售淡季，农资使用数量下降，在季节性作用下，农资价格到达全年最低点。

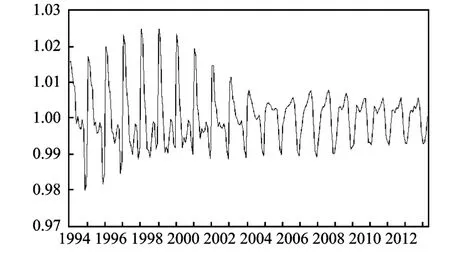
图1 农资价格季节性波动分解序列图

图1还可以看出，20年间，农资价格的季节振荡幅度在逐年递减，尤其是2005年后衰减最为明显，说明季节因素的作用在逐渐降低。对此可能的原因主要是库存的缓冲作用。为缓解农资市场供需的季节性矛盾，国家从2005年开始建立化肥等大宗农资商品淡季储备制度，通过“淡季储备，旺季调节”，一定程度上弱化了农业生产季节性对农资价格的影响，从而保证了农资价格波动趋于平稳的发展态势。观察波峰、波谷的变化情况可看出，1994—2001年，农资价格波动的波峰一直为1月份，从2002年开始逐年后移，其中2002—2004年变2月份，2005—2009年变为8月份，2010年以来则变为9月份，呈现愈发明显的双波峰态势；从波谷的变化情况来看，1998年之前波谷均出现在11月份，1998—1999年向前提到7月份，而从2000年开始12月份成为新的波谷并趋于稳定。

（二）农产品价格波动的周期性特征

在季节调整的基础上进行HP滤波分解，并根据剩余测定法依次剔除季节成分、趋势成分和不规则成分之后，得出农资价格波动的周期成分，如图2所示。从中可以看出，样本期间，剔除了其他因素影响，仅受周期性波动影响的农资价格大约经历了五个完整周期（“波谷”到“波谷”），分别是1994年1月至1998年6月、1998年7月至2003年8月、2003年9月至2007年4月、2007年5月至2010年7月和2010年8月至2014年3月，平均价格周期长度在48个月左右。

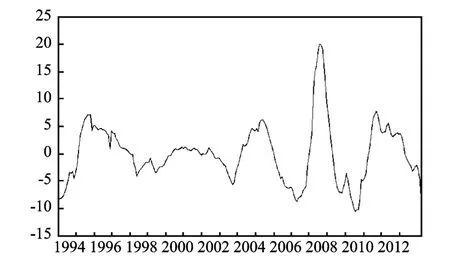
图2 农资价格周期性波动分解序列图

结合表2可知，农资价格的这种周期性波动具有以下两个趋势性特征：一是起伏周期变短，波动幅度增大。2003年以前的两个波动周期虽然都较长，分别为54个月和64个月，但波动的幅度都较小，波距（等于波峰到波谷的距离）分别为11．336 2和6．911 7；随后的波动周期明显有缩短倾向，且波动幅度要大于之前的两个周期。二是收缩期长于扩张期，波动逐步由对称周期向非对称性周期转变。尤其是2003年以后的三个波动周期，波峰出现较早，且收缩期下降幅度比扩张期上涨幅度平缓，直接造成了农资价格“上涨容易下跌难”的事实。

表2 农资价格波动的周期特征表

对HP滤波分解的效果进行评价。在评价中可以把是否将时间序列脱离趋势以后平稳化作为衡量不同分解方法优劣的基本准则，检查序列平稳性的方法用单位根检验［14］。对经过HP滤波后得到的周期成分Ct进行ADF检验，结果显示，周期成分Ct的ADF统计量值为－4．263 559，小于1%显著水平下的临界值－2．574 633，所以拒绝存在单位根的原假设，即周期成分Ct是平稳的。因此，可认为HP滤波分解所得到的周期成分能够反映农资价格波动的真实周期特征。

（三）农资价格波动的聚集性、非对称性特征

对原始数据季节性、周期性特征的分析，从某种程度上能反映出农资价格波动的聚集性以及隐含着的非对称性，下面进一步应用EGARCH－M模型进行检验。表3是针对农资价格收益率，其中和分别表示第t期和第t－1期的农资价格指数）进行的描述性统计。由表3可知，农资价格收益率的偏度大于0，略左偏；峰度高于正态分布的峰度值3，呈现出尖峰后尾特征。JB正态性检验显示，农资价格收益序列在1%的显著性水平上拒绝了服从正态分布的零假设，这意味着其分布是非正态的。ADF检验显示，在1%的显著性水平下拒绝存在单位根的假设，说明农资价格收益率是平稳的。检验序列自相关性的Q统计量结果表明，农资价格收益率存在显著的自相关性，因此可以考虑用自回归移动平均（ARMA）方程来描述它。而用来检验序列相关性的Q2统计量的结果又显示，农资价格收益率还存在条件异方差和波动集聚现象，因此还需要用ARCH类模型进行拟合。

表3 农资价格收益率序列的统计特征表

首先用ARMA过程来描述序列Rt的自相关性。对Rt进行相关性检验，发现其自相关系数是拖尾的，而偏相关系数在2阶截尾，然后依据SC最小值准则来确定模型的最优阶数，经反复筛选，最终决定选取AR（2）模型来描述序列Rt的变化：

然后采用条件异方差的ARCH－LM检验该AR（2）模型的残差是否存在ARCH效应。检验发现，农资价格收益率序列异方差效应显著，取滞后阶数p为1～4时的相伴概率都小于显著性水平α＝0．05，即存在高阶ARCH效应，而由于一个高阶的ARCH模型可以用一个低阶的GARCH模型代替，因而此处考虑加入GARCH模型。

大多数研究者发现，对于尖峰厚尾的非正态分布，用一个简单的GARCH（1，1）模型就能进行刻画。因此在建模时，首先选取p＝q＝1，若模型中的GARCH（1）项系数在5%的水平上不显著，或即使显著但ARCH（1）项系数与GARCH（1）项系数之和大于1，则说明模型不稳定，此时调整p和q的值，并根据AIC和SC最小信息准则确定最优参数。经反复比较，选择用GARCH（2，1）模型对农资价格收益率序列进行建模。本文在GARCH（2，1）的基础上加入了非对称性和高风险高回报的特征，因此采用EGARCH（2，1）－M 模型。又已知序列Rt有尖峰厚尾的特征，与正态分布存在显著差异，因此，本文还对比了正态分布、T分布和GED分布三种情况下的模型拟合情况（见表4）。

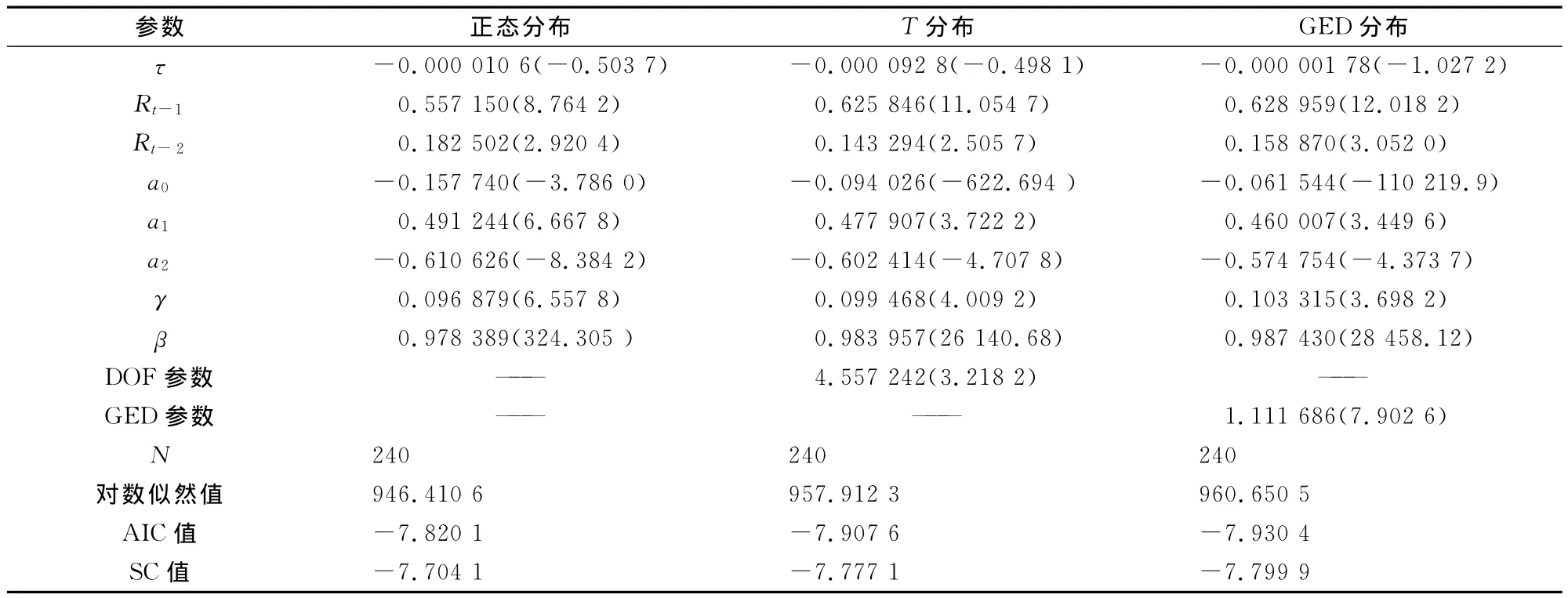
表4 EGARCH（2，1）－M模型参数估计结果表

估计结果表明，无论是从对数的似然值来看，还是从AIC和SC信息最小准则来看，GED分布都能更好地拟合模型。此外，从EGARCH（2，1）－M 模型的输出结果看到，GED分布的参数小于2，验证了使用GARCH类模型对农资价格收益率序列建模时所得残差项的厚尾特征，表明GED分布能够很好地描述这种特征。对基于GED分布的EGARCH（2，1）－M 模型的残差进行 ARCH－LM 检验，结果表明，残差序列不存在ARCH效应。因此，下面主要基于GED分布下EGARCH（2，1）－M 模型参数估计结果进行相关分析。

首先，均值方程中，τ的估计值几乎为0，且不显著，反映了中国农资市场并不具备高风险高收益的市场经济特征，这与中国农资行业竞争不充分、政府对农资实行“专营”和“限价”政策的现实是非常相符的。

其次，条件方差方程中，参数β都在1%的水平下显著，表明农资价格收益率序列具有显著的波动聚集性。关于波动聚集性产生的原因，鉴于目前中国农资市场尚未完全市场化运作，也尚未与宏观经济形成高度相关的互动机制，本文更倾向于结合Harris、Raviv和Shalen提出的理念分散模型来解释［15－16］。自农资供给体制市场化改革以来，中国农资供给呈现“大行业、小企业”的格局，农资供需链中的生产经营主体不断增加，但多数是个体承包，点多、面广且分散，既不能及时准确掌握市场信息，彼此之间又缺乏相应的联系，市场一有风吹草动就“一哄而上、一哄而下”，造成市场均衡的脆弱性和市场进入的盲目性，增加了聚集波动产生的可能性。

最后，非对称项系数γ为正且在1%水平上显著，说明农资价格的波动存在杠杆效应，并且是正向冲击对农资价格波动的影响要比负向冲击的大。具体而言，当农资市场受到负向冲击时，会给条件方差对数带来0．356 7倍冲击，而当受到正向冲击时，会给条件方差带来0．563 3倍冲击。图3是描述GED分布下EGARCH（2，1）－M模型拟合农资价格收益率数据的信息冲击曲线，从中也可以看出，正向冲击使得农资价格波动性的变化更大一些。从经济学角度讲，农资价格波动的这种非对称性根源于农资供求双方市场地位的严重不对等。从供给方看，中国的农资生产和进口较为集中，大型的生产和进口企业往往具有垄断性，可以凭借其垄断地位操控农资出厂或一级批发价格；而从需求方来看，主要是极其分散和高度同质的千千万万个小规模农户，由于固有的种植习惯、土地种植特性，即使当市场价格出现下跌迹象时也很难及时做出重大的种植改变，对价格变化的反应不是很敏感，在大多数情况下，只能被动接受价格。农资供求双方市场地位的这种不对等，不仅直接造成了农资价格“上涨容易下跌难”的事实，而且价格上涨信号会通过“羊群效应”引起农民争相抢购农资，加剧了价格进一步上涨，加上投机因素的推波助澜，最终使得上期价格上涨信息引发的波动大于下跌信息所引发的波动。

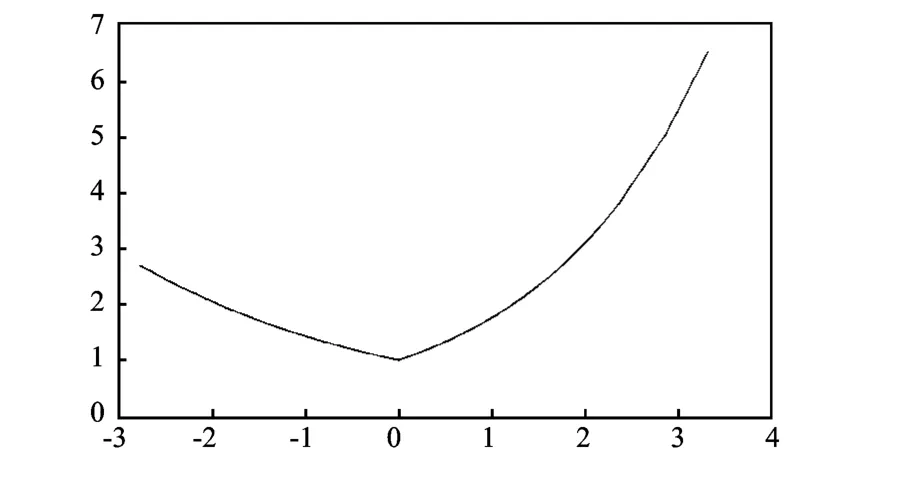
图3 农资价格信息冲击曲线图

四、结论与启示

综合以上分析，本文得到以下几点结论：

1．中国农资价格存在显著的季节性波动，每年11—12月份为季节性波谷，9月份为季节性小波峰，2月份为大波峰。并且这种季节性结构非常不稳定，有随年份的推移而波峰不断后移的趋向。建议政府将主要农资商品淡储起止时间做适当调整或后延，以防止因季节性因素导致的农资价格过快上涨。

2．农资价格波动还具有明显的周期性特征。根据HP滤波分解结果，近20年来农资价格大约经历了五个完整波动性周期，平均周期长度在48个月左右。农资价格波动表现出的这种周期性，要求政府对农资价格的调控应遵循自然周期，允许价格在一个适度的区间内波动，减少“急刹车式”的频繁调控和对供给端的过度干预，保证市场的充分性和有效性，用市场化手段解决农资产品价格波动问题。

3．农资市场没有体现出高风险高回报的市场经济特征，验证了中国农资市场尚未完全市场化运作。目前政府对农资实行限价政策，农资的出厂和销售都处在监管之下，但从实践情况来看，这不仅没有很好地控制住农资价格的大幅上涨，反而抑制了行业的供给扩张。事实上，农资应当是一种不具有自然垄断属性的普通产品，只是在消费领域，因与农民收入及农业生产密切相关，具有相当的战略属性。因此，政府对农资价格的监管应实行区别对待的政策。单就生产领域来讲，政府应考虑放宽行业管制，取消限价制度，让农资市场充分市场化。只有充分市场化，造就充分竞争的外部环境，资源配置才会更加有效，也才能更好地实现供求均衡。

4．农资市场具有很强的波动集聚性，大的价格波动后面往往跟随着大的价格波动，小的价格波动后面经常跟随着小的价格波动。这就给了我们在预防农资价格波动方面提供了很好的启示，即农资市场一旦出现了能够引起较大波动的因素时，就要做好应对连续波动的准备；要加强对主要农资价格的监测，密切关注市场动态，及时发现苗头性趋势。

5．对农资价格而言，供给不足时价格的上涨幅度要大于供给相对过剩时价格下降的幅度，折射出中国农资市场上供求双方之间严重不对等的市场地位，供给方的市场地位明显优于需求方。因此，改变由农资生产和进口企业垄断的农资市场结构，促进农资市场由垄断性市场向竞争性市场转变，应是中国深化农资市场化改革的基本取向。

6．模型结果显示，GED分布模型能更好地描述和拟合农资价格的波动特征。由于农资价格收益率序列具有显著的尖峰厚尾、非正态分布特征，使用正态分布的假设来估计模型会存在明显的不足。本文通过比较正态分布、T分布和GED分布下的EGARCH－M模型的对数似然值、AIC和SC信息准则，发现基于GED分布的模型拟合效果最好，可以更好地分析中国农资价格的波动特征。

［1］铺甫宁，谢正勤．生产资料市场化改革对农业结构调整的作用［J］．华中农业大学学报：社会科学版，2002（1）．

［2］王侃，汪波．中国化肥的需求价格弹性分析［J］．中国农机化，2007（5）．

［3］王新志．通胀压力下农资价格上涨的应对策略研究［J］．山东农业大学学报：社会科学版，2008（4）．

［4］金赛美．农业生产资料价格指数与通货膨胀率的相关分析［J］．西安财经学院学报，2010（6）．

［5］韩艳旗，王红玲．新形势下农资价格大幅上涨对“三农”的影响分析［J］．华中农业大学学报：社会科学版，2008（6）．

［6］李正辉，徐亚丽．农产品价格波动的非对称性研究［J］．湖南大学学报：社会科学版，2014（1）．

［7］庄岩．中国农产品价格波动特征的实证研究——基于广义误差分布的ARCH类模型［J］．统计与信息论坛，2012（6）．

［8］黄文彪，徐学荣，郑思宁．基于ARCH类模型的中国农资价格波动特征分析［J］．中国农学通报，2012（20）．

［9］马凯，潘焕学．中国农业生产资料价格波动特征及影响因素的分析［J］．价格理论与实践，2013（10）．

［10］张文雄．中国化肥价格波动趋势及影响因素的实证研究［J］．价格理论与实践，2014（3）．

［11］Engle R F．Autoregressive Conditional Heteroskedasticity with Estimate of the Variance of U．K．Inflation［J］．Econometrica，1982（50）．

［12］Tim B．Generalized Autoregressive Conditional Heteroskedasticity［J］．Journal of Econometrics，1986（31）．