递归均值调整单位根检验能提高检验功效吗？

江海峰，崔立志，汪忠志

（安徽工业大学a．商学院；b．数理学院，安徽 马鞍山243002）

一、引 言

自从Phllips在1986年从理论上证明单位根可以产生伪回归以来，单位根检验已在实证研究中引起重视，单位根检验理论也日益丰富［1］。作为一种假设检验，单位根检验也同样会犯两类错误，但单位根检验有其特殊性：首先，单位根检验统计量分布不但与数据生成过程有关，还取决于检验模型设定形式［2－3］；其次，除个别情形之外，绝大多数单位根检验统计量分布收敛到维纳过程的泛函，且分布收敛都建立在大样本前提下，有限样本下分布并不存在。这种特殊性对单位根检验的两类错误必然会产生影响。为降低第一类错误，研究人员将Bootstrap方法引入到单位根检验中，取得了良好效果，但对提高检验功效的作用并不明显［4－5］。为提高检验功效，Shin和So于2001年将递归均值调整方法引入单位根检验中［6］。其检验思路如下：设数据生成模型和检验模型分别为下列式（1）和式（2）：

其中），建立假设。经典第二类DF检验①①照陆懋祖的分类标准，将单位根DF检验分成四类：第一类和第二类DF检验数据生成为无漂移项的随机游走过程，而检验模型分别与式（1）、式（2）相对应；第三类和第四类DF检验与本文研究无关，具体介绍参见陆懋祖的介绍［7］57－76。参数估计为：

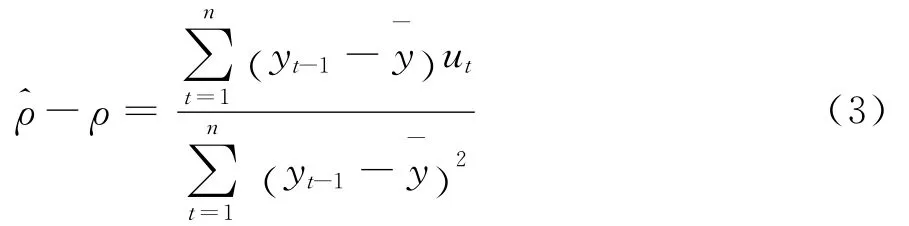
显然，这种偏差随着ρ0靠近1而逐渐变大，进而降低单位根检验功效。为消除偏差，Shin和So更改检验模型（2）的设定形式如下：

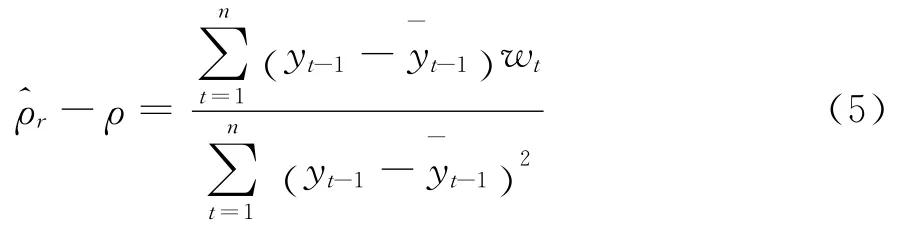
Shin和So的模拟表明：对于同样的真值ρ0，和式（3）相比，引入递归均值以后，比更加接近真实值ρ0，偏差改进程度约为（1＋ρ0）／n。因此，对于较大的ρ0或者较小的样本n，递归均值方法确实可以降低估计偏差，使得递归均值调整下检验统计量的临界值右偏，从而提高检验功效。此后Cook使用递归均值调整方法讨论结构突变单位根检验模型，也得到类似结论［9］。Rodrigues等进一步研究递归趋势调整单位根检验模型，但没有和对应的DF检验模式进行比较，也没有推导检验统计量的渐进分布［10－11］。

引入递归均值真能够提高检验功效吗？正如上文所提到的那样，单位根检验功效同时取决于数据生成过程和检验模型设定形式。实际上，Shin和So在所有模拟中，都假设μ＝0，当原假设H0：ρ＝1成立时，由式（4）可知，无论μ＝0是否成立，对模拟均不产生影响，但当μ≠0且备择假设成立时，模型（4）表示均值为μ的平稳过程，对于此种情况下的检验功效，他们并没有给出结论。从可比性角度来说，当备择假设成立时，μ＝0意味着序列为零均值平稳过程，如果使用DF检验，则应该与第一类DF检验而不是第二类DF检验比较功效；如果从误设检验模型形式来说，即错误选择带漂移项检验模型，但均值仍为零，此时可以比较递归均值调整检验模式与采用全样本均值 调整的第二类DF检验模式。显然Shin和So仅比较了后者，而忽略了前者，由此得到的结论缺乏普遍性。

当μ≠0时，还可以从双模型数据生成角度来理解式（4）。类似式（2）那样，经典DF检验将均值和单位根生成过程融入一个模型中，而Bhargava主张使用两个模型表示各自的生成过程［12］。例如与式（2）对应的数据生成过程用双模型表示如下：

当μ＝0时对应Shin和So的结论，当μ≠0且ρ＝1－c／n（c＞0）为近单位根时，模型（4）表明yt是均值为μ的平稳过程，这也正是模型（6）表示的含义。相对于第二类DF检验模式，等价于模型（2）中δ＝n－1cμ≠0且ρ＝1－c／n，这时也可以比较第二类DF检验与递归均值调整检验下的检验功效，显然Shin和So也没有对此进行研究。

因此，要全面比较递归均值调整检验与经典DF检验的功效，就必须从检验模型设定形式以及均值μ取值是否为零两个角度出发，在保持可比性基础上进行全面分析，即应该研究以下3个内容：

（1）真实均值μ＝0，比较正确使用第一类DF检验和递归均值调整检验的功效；

（2）真实均值μ＝0，比较误用第二类DF检验与递归均值调整检验的功效；

（3）真实均值μ≠0，比较正确使用第二类DF检验与递归均值调整检验的功效。

显然，Shin和So只研究了其中的内容（2）。因此，本文就按照这个思路展开研究，首先导出各种情况下检验功效公式，然后再通过蒙特卡罗模拟来估算有限样本下的检验功效，最后给出研究的最终结论。

二、零均值数据生成模型检验功效

（一）第一类DF检验

如果数据生成与检验模型都不含有漂移项，此时对应第一类DF检验，根据式（1）有：

当H1：ρ＝1－c／n成立时，递推式（1）有，其中 ，且有成立，［nr］表示不超过的正整数，）。利用结论得到，根据 Phillips的研究有［13］：

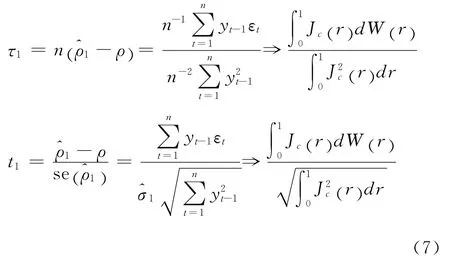
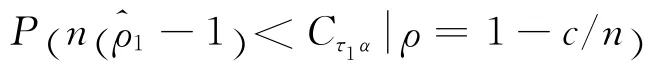
其中Cτ1α和Ct1α是式（7）当c＝0时检验统计量τ1和t1对应显著性水平为α的临界值）为标准差。式（8）等号左边给出了检验功效的模拟计算公式，而等号右边给出了功效计算的理论公式（下同）。这就导出了研究内容（1）中第一类DF检验统计量的功效公式。

（二）递归均值调整检验

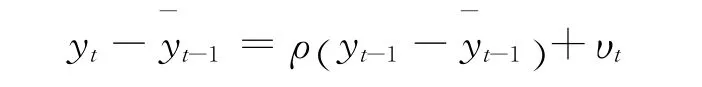
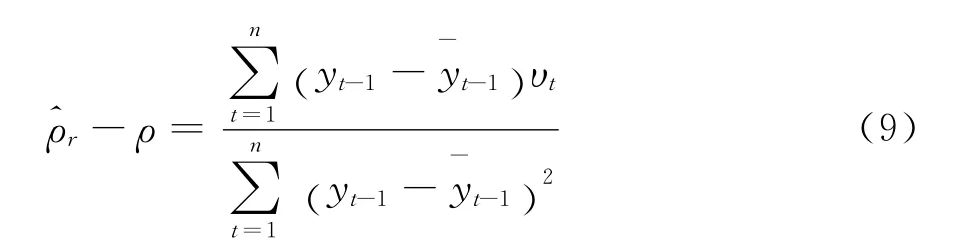
建立检验统计量为：

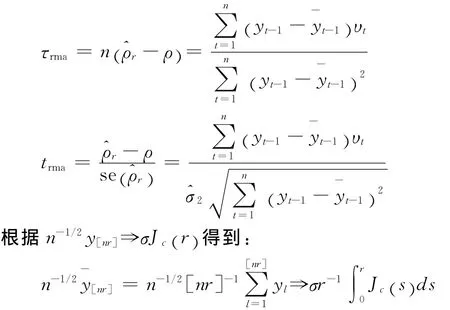
根据Kurtz和Protter在1991的研究有［14］：

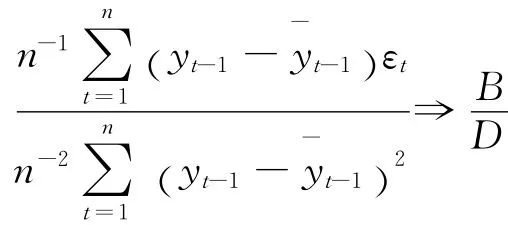
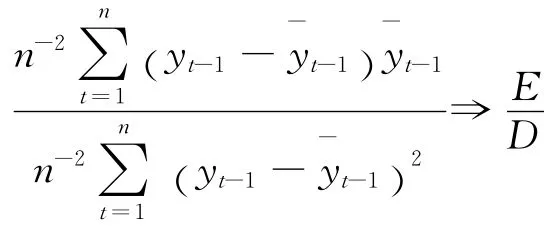
其中：

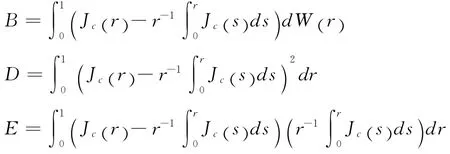
因此得到：

从而采用递归均值调整模式时检验功效为：

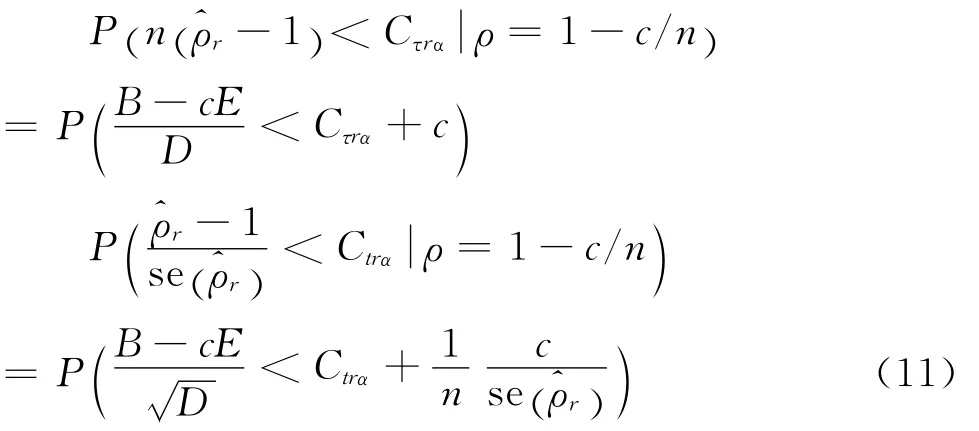
（三）第二类DF检验

如果采用第二类DF检验模式，即采用如下检验模型：

根据最小二乘法有：

利 用 结 论 n－1／2y［nr］σJc（r）得 到，带入式（12）有：

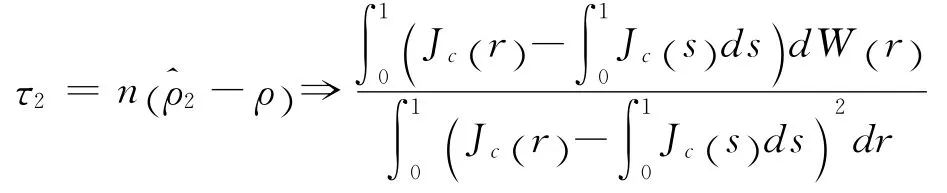
三、非零均值数据生成模型检验功效

实际上，Shin和So的理论研究中并没有要求μ＝0，下面分两种情况讨论其检验功效。

（一）单方程第二类DF检验

为得到含有非零均值平稳序列，就需要假设式（2）中δ≠0。为和式（6）表示的模型具有可比性，必须保证在原假设成立时有相同的均值，因此有δ＝（1 －ρ）μ。当备择假设H1：ρ＝1－c／n成立时，根据式（2）结合δ＝ （1 －ρ）μ 递推得到：

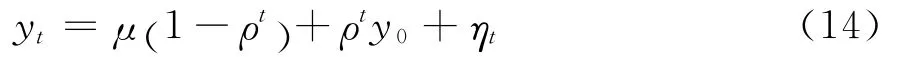
（二）双方程递归均值调整模型检验

当使用数据生成式（6）来考察非零均值单位根过程或者平稳过程时，消除xt可得到式（4），此时仍使用递归均值进行调整得到检验模型为：

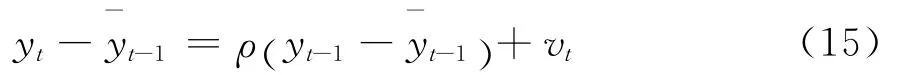
因此有：

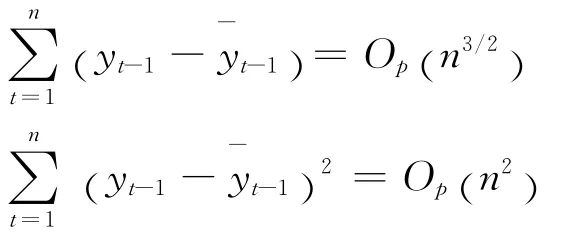
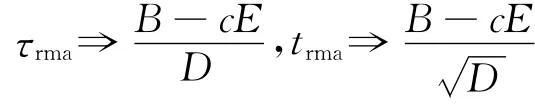
从而检验功效仍为式（11）。这就导出了内容（3）中递归均值调整检验统计量的功效公式。

同样需要说明的是：均值μ是否为零不影响检验功效理论公式的原因在于式（16）中第二项为，对分布的影响在大样本下可以忽略，但在有限样本下仍有差异。

四、检验功效的蒙特卡洛模拟分析

（一）模拟设置

为比较递归均值调整模式与DF类检验模式下的检验功效，现进行蒙特卡洛模拟分析。设模拟次数为10 000次，取样本容量为25、50、100和250，显著性水平为0．05，εt服从标准正态分布，ρ分别取1、0．95、0．90、0．85和0．80，μ按照研究内容分别设置μ＝0和μ≠0两种情况。

（二）零均值数据生成与模拟

首先比较均值μ＝0时第一类DF检验、第二类DF检验和递归均值调整检验的模拟结果，表1给出了模拟结果。当μ＝0且备择假设成立时，数据生成都是零均值平稳过程，根据研究内容（1）和研究内容（2）可知，此时第一类DF检验、第二类DF检验分别与递归均值调整检验的功效具有可比性。表1表明：当ρ＜1时，对于相同的ρ和样本容量，递归均值调整模式检验统计量τrma、trma的检验功效都高于第二类DF检验对应检验统计量τ2、t2，这与Shin和So的结论完全一致，却明显低于第一类DF检验对应检验统计量τ1、t1，这是他们没有发现的结论。从这个角度来说，不能完全接受递归均值调整检验模式能够提高检验功效。另外，表1也显示，对于相同的ρ，随着样本n增大，每种检验统计量检验功效呈现递增趋势；对于相同样本容量n，随着ρ降低，每种检验统计量检验功效也呈现递增趋势，这可以从ρ＝1－c／n中得到解释，因为上述两种情况都会导致c呈现递增趋势，而上文各个检验功效计算公式都表明检验功效随着c递增而递增。

表1 零均值调整和DF检验的功效模拟结果

另外，表1还给出了此种情况第一类DF检验、第二类DF检验以及递归均值调整检验的检验水平模拟结果，这对应ρ＝1的取值。由于模拟的随机性，每种检验的实际显著性水平不可能正好等于名义水平0．05。根据Godfrey和Orme提供的实际显著性水平区间估计公式，取概率度为1．96得到实际显著性水平的区间估计为（4．60%，5．40%）［15］。显然，这些检验统计量的检验水平均落在该区间估计内，因此具有满意的检验水平，从而在此基础之上的检验功效比较是有意义的。

（三）非零均值数据生成与模拟

接下来考察当μ≠0时各个检验统计量检验功效。直观地认为，当μ与0差距不大时，相关检验结论应该与μ＝0结果大体相同，为了考察μ的变化对各检验统计量检验功效的影响，同时鉴于经济时间序列中的μ＞0，本文考察μ从1到10每次递增0．5时的功效，表2～5只给出了上述4种样本下μ取值为1、5和10时各个检验统计量的检验功效和检验水平。

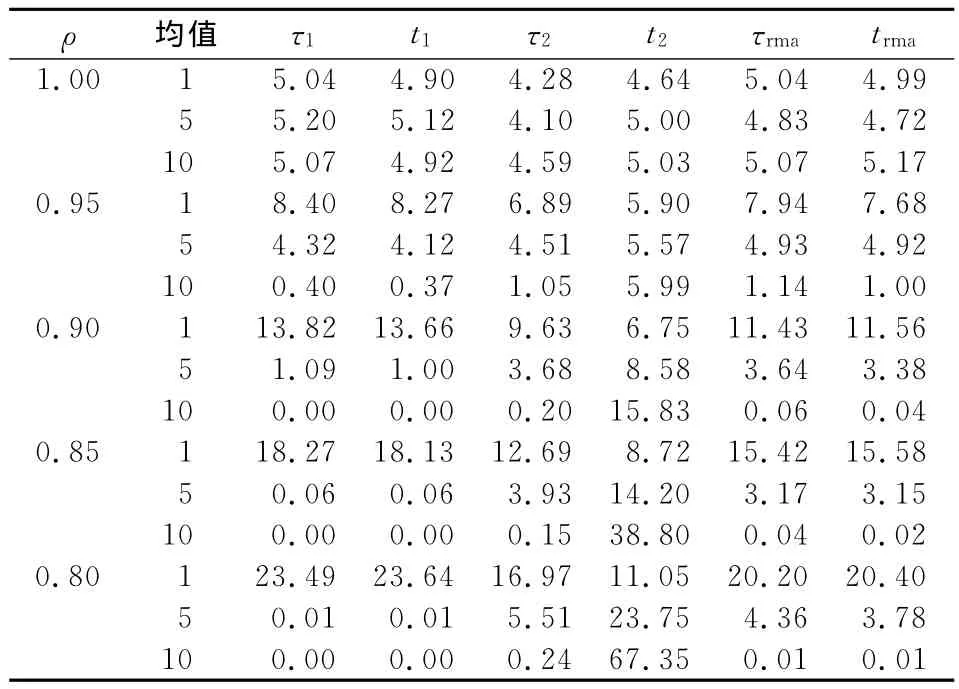
表2 样本为25时均值调整和DF检验的功效模拟结果

表3 样本为50时均值调整和DF检验的功效模拟结果

根据研究内容（3）可知，此时第一类DF检验没有可比性，而第二类DF检验和递归均值检验模式在备择假设成立时都表示非零均值的平稳过程，具有可比性。表2和表5显示：当μ＝1且ρ＜1时，对于相同的ρ和样本容量，递归均值调整模式的检验统计量的检验功效都高于第二类DF检验对应检验统计量；当μ＞1时，除样本容量为25和250且ρ＝0．95之外，其它参数组合下，第二类DF检验对应检验统计量的检验功效都不低于递归均值调整下对应检验统计量的检验功效。因此，当μ≠0时，递归均值调整模式下检验功效也不是始终最高。

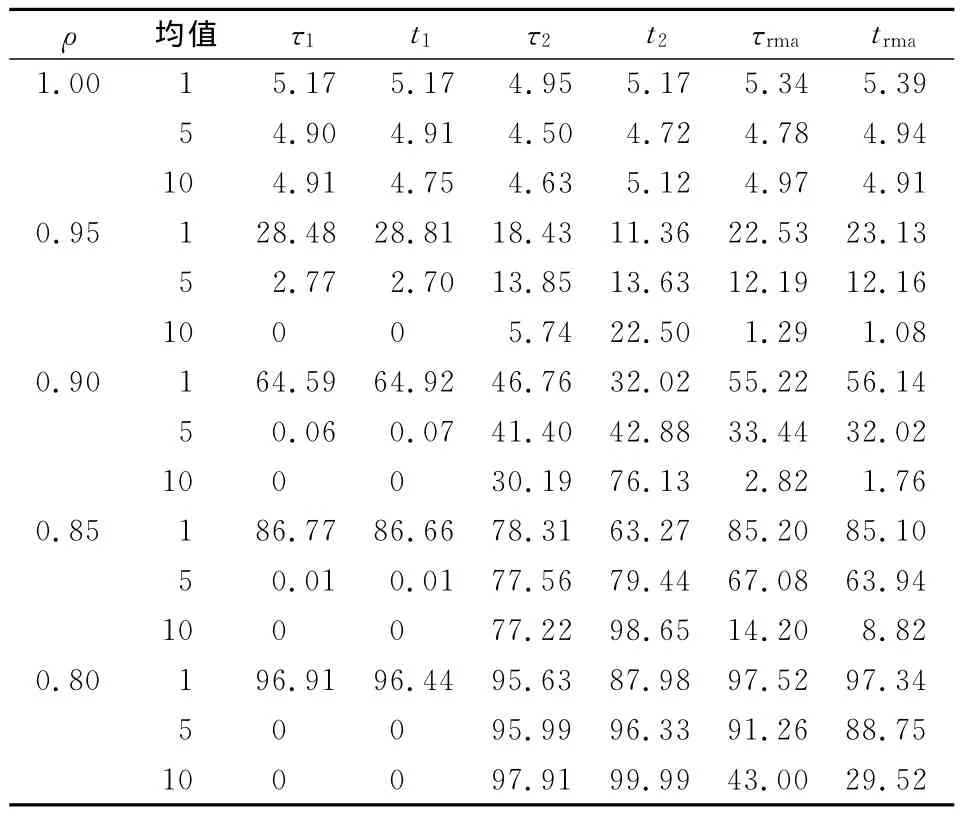
表4 样本为100时均值调整和DF检验的功效模拟结果

另外，除表2中有一处检验水平没有落在上述理论检验水平区间估计之外①①表5中的检验统计量tdf1也有一处不满足上述区间估计要求，但因不具备可比性而不予考虑。（用黑体表示），表2和表5中第二类DF检验统计量和递归均值检验统计量的其它场合检验水平都很好地落入到理论检验水平的区间估计内，因此上述的检验功效比较也是有意义的。

表5 样本为250时均值调整和DF检验的功效模拟结果

为反映出μ取值对检验统计量功效的影响，下面以第二类DF检验和递归均值调整检验模式的伪t检验统计量为代表，给出检验功效、样本容量和ρ取值的三维图形，结果如图1～8所示，其中纵轴表示检验功效，取值为0至1；标有4个刻度坐标轴表示ρ取值，分别为0．80、0．85、0．90和0．95；取值从1到10的轴表示均值μ变化过程。图1、图3、图5和图7对应第二类DF伪t检验统计量4种样本的检验功效图，而图2、图4、图6和图8表示递归均值调整伪t检验统计量4种样本的检验功效图。显然，对固定的μ，两类检验模式的检验功效随着ρ增加呈递增趋势，但当固定ρ，对于第二类DF检验来说，检验功效随着μ增加呈递增趋势，但对均值调整检验模式来说，检验功效却随着μ增加呈递减趋势，但当样本为250时两类检验模式的检验功效都达到最大值。类似的结论也适用于两类检验模式的系数检验统计量。因此，综合表2～5以及图1～8的结果，不难看出，当μ＞0时，第二类DF检验统计量的检验功效在大多数场合下要高于均值调整递归检验模式下的检验功效。

图1 样本为25第二类DF伪t检验统计量功效图

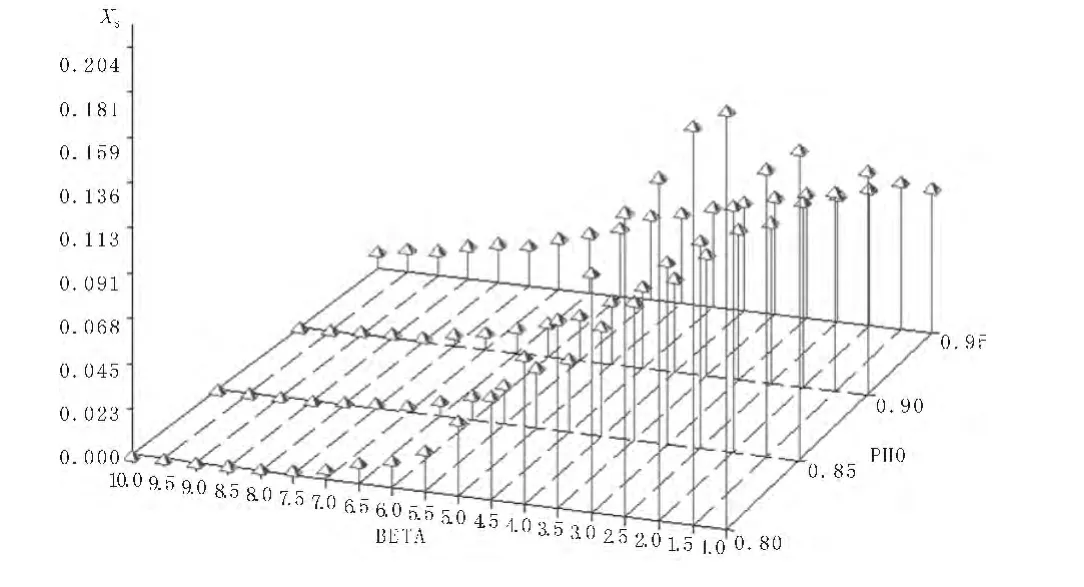
图2 样本为25递归均值调整伪t检验统计量功效图

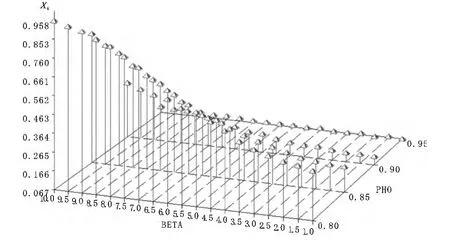
图3 样本为50第二类DF伪t检验统计量功效图

图4 样本为50递归均值调整伪t检验统计量功效图

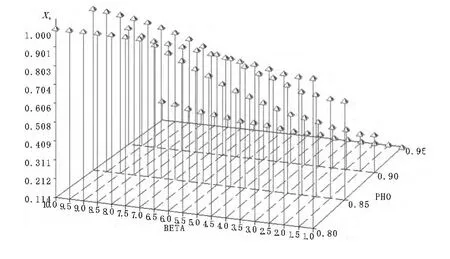
图5 样本为100第二类DF伪t检验统计量功效图

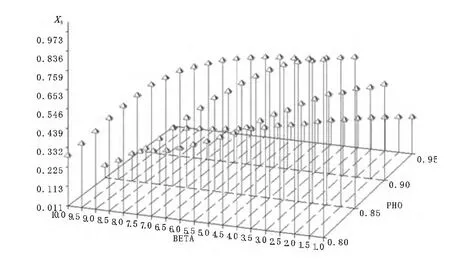
图6 样本为100递归均值调整伪t检验统计量功效图

图7 样本为250第二类DF伪t检验统计量功效图

图8 样本为250递归均值调整伪t检验统计量功效图

五、结 论

综上分析，本文得到以下四点结论：

1．当原假设成立表示单位根过程而备择假设成立表示平稳过程时，无论平稳过程的均值是否为零，第二类DF检验功效理论公式相同，递归均值调整模式检验功效理论公式也与均值是否为零无关，但这仅限于大样本情况下的结论，而有限样本下结论不成立，模拟结果验证了这点。

2．当序列表示为零均值平稳过程时，第一类DF检验模型为正确设定形式，而第二类DF检验和递归均值调整检验模式，为模型误设形式，三种检验模式满足可比性原则，模拟结果表明：此时递归均值调整检验模式的检验功效高于第二类DF检验模式，但低于第一类DF检验模式，这表明对于零均值的平稳过程而言，递归均值调整检验模式检验功效并非最高。

3．当序列表示为非零均值的平稳过程时，第一类DF检验模型为误设形式，而第二类DF检验和递归均值调整检验模式为正确模型形式。此时只有后两种检验模式满足可比性原则，模拟结果表明，递归均值检验功效的优势仅限于较小的非零均值，对于较大均值，第二类DF检验模式的检验功效具有优势。

4．无论均值是否为零，各种检验统计量的实际检验水平与名义检验水平完全吻合，因此上述有关检验功效的结论得到检验水平结果的支持。

综上所述，在实证分析中，应结合序列均值的判断，谨慎使用递归均值调整模式进行单位根检验。

［1］ Phillips P C B．Understanding Spurious Regressions in Econometrics［J］．Journal of Econometrics，1986（3）．

［2］ 陶长琪，江海峰．二次趋势模型的误设检验与仿真分析［J］．统计与信息论坛，2012（3）．

［3］ 白仲林，赵嫣．检验式设定错误对时间序列单位根检验小样本性质的影响［J］．统计与信息论坛，2008（4）．

［4］ 江海峰，陶长琪，陈启明．ADF模式中漂移项和趋势项检验统计量分布与Bootstrap检验研究［J］．统计与信息论坛，2014（7）．

［5］ 刘汉中．残差块形自助法在非对称单位根检验中的适用性［J］．统计与信息论坛，2010（2）．

［6］ Shin D W，So B S．Recursive Mean Adjustment for Unit Root Tests［J］．Journal of Time Series Analysis，2001（5）．

［7］ 陆懋祖．高等时间序列经济计量学［M］．上海：上海人民出版社，1999．

［8］ Shaman P，Stine R A．The Bias of Autoregressive Coefficient Estimators［J］．Journal of the American Statistical Association，1988，83（403）．

［9］ Cook Steven．Correcting Size Distortion of the Dickey－Fuller Test Via Recursive Mean Adjustment［J］．Statistics ＆Probability Letters，2002（6）．

［10］Rodrigues P．Properties of Recursive Trend－Adjusted Unit Root Tests［J］．Economics Letters，2006（3）．

［11］Eddy Lizarazu Alanez，JoséA，Villase or Alva．Ajuste Recursivo Con Transformaciones Invariantesy Bootstrapping：El Caso de Una Caminata Aleatoria Con Intercepto［J］．Econo Quantum，2010（1）．

［12］Bhargava A．On the Theory of Testing for Unit Roots in Observed Time Series［J］．Review of Economic Studies，1986，53（3）．

［13］Phillips．Towards a Unified Asymptotic Theory for Autoregression［J］．Biometrika，1987，74（3）．

［14］Kurtz T G，Protter P．Weak Limit Theorems for Stochastic Integrals and Stochastic Differential Equations［J］．The Annals of Probability，1991，19（3）．

［15］Godfrey L G，Orme C D．Controlling the Significance Levels of Prediction Error Tests for Linear Regression Models［J］．Econometrics Journal，2000（1）．