盘磨机磨浆区有效能耗浅析

王佳辉

（天津科技大学机械工程学院，天津，300222）

回转机械的摩擦力矩是影响机械系统的效率、输出功率的重要因素。将盘磨机看作一种低速、低效的离心泵，磨浆区作为盘磨机磨浆部分，消耗的功率占总功率的主要部分。本文介绍了采用摩擦力矩理论推导盘磨机磨浆区有效能耗的方法，在此基础上介绍了一种新的计算模型，实际应用还有待于进一步研究。正确估计盘磨机的摩擦力矩并分析其中参数对能耗的影响，对控制磨浆过程、改善磨浆条件、提高磨浆质量都有重要意义。

1 有关磨区摩擦的基本理论

盘磨机磨区内的摩擦是个动态不稳定过程，其摩擦机理较为复杂。分析计算盘磨机磨区内摩擦时，混合了各种摩擦如半干摩擦 (同时存在干摩擦和边界摩擦)和半流体摩擦(同时存在流体摩擦和边界摩擦)。普遍认为盘磨机摩擦状态可以由以下几种摩擦机理解释：油膜剪切摩擦机理，边界摩擦机理和混合摩擦机理[1]。

1.1 油膜剪切摩擦机理

油膜剪切摩擦又叫做液体摩擦，其机理是依靠液体膜之间的剪切力来传递力和力矩。理论认为磨片之间没有实质性的接触，忽略了磨片齿纹的影响，认为仅是依靠边界油膜的剪切传力，所以无法解释磨片表面存在磨损的事实。

1.2 边界摩擦机理

边界摩擦机理的典型模型是Bowden边界摩擦机理模型。Bowden等人从表面凹凸不平观点出发，提出了新的边界摩擦理论，这种模型的摩擦状态实际上是由干摩擦(直接接触)、边界摩擦(边界膜剪切)以及液体摩擦(油膜剪切)组成的混合摩擦，考虑了磨片齿纹对摩擦的影响。

1.3 混合摩擦机理

混合摩擦机理，认为犁沟效应是产生摩擦的主要原因。混合摩擦机理主要考虑犁沟效应产生的摩擦效果，适用于磨片间距较小的情况，对于间距较大的情况，摩擦力仍然存在，其摩擦磨损的机理无法利用单一的混合摩擦机理给予科学的解释。

从经典的摩擦机理入手，分析了盘磨机摩擦片摩擦过程中涉及到的3种摩擦状态，给建立的各种盘磨机能耗的模型提供参考，对于磨片的设计、制造提出了更加准确的理论依据。

2 盘磨机求有效能耗的方法

2.1 实验法

利用实验数据测量磨浆过程消耗能量，根据实验得出的浆料单位时间通过量、盘磨机工作电压、电流、磨浆度、循环次数等数据，可以估算出对应的用于磨浆的能耗。经验公式[2]为：

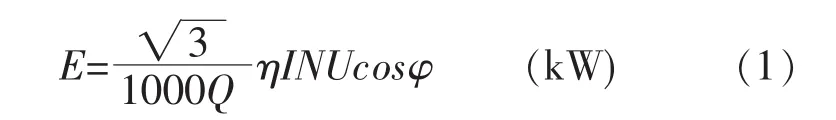
式中：E 为磨浆能耗(kWh·t-1)；I为磨浆电流(A)；U为工作电压(V)；N为浆料通过次数；Q为浆料单位时间通过量 (t·h-1)；cosφ 的取值范围为 0.85～0.90；η的取值范围0.75～0.90。

2.2 摩擦力矩法

刘靖[3]在文献中指出盘磨机工作时，假设两磨片是理想平面，比压P在整个磨片面上为常数，故整个面上的磨擦力矩为：

其中R1、R2分别为磨片外径和内径，m；P为油缸作用于动盘面压力，Pa；Cr、Cs分别为定、动磨片平均接触率；u为磨浆阻力系数。

由油缸比压p和推力F之间的关系F=π(R12-R22)P代入上式，得到的克服上述磨擦力矩所消耗功率为：

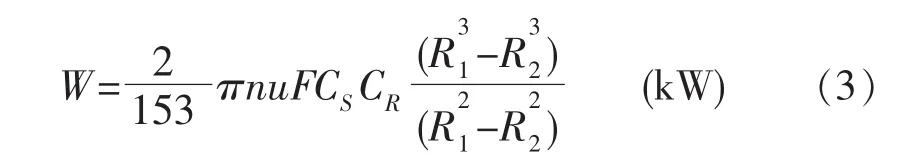
李世扬[4]在文献中提出的摩擦力矩方法引入了参数 r、g， 其中 r为浆料密度，kg·m-3，g 为重力加速度，m·s-2，得出的消耗功率计算公式为：

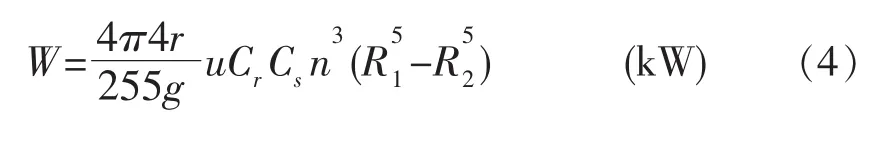
2.3 磨盘分区法

Mirja Illikainen等[7]介绍了一种磨盘分区计算能耗的方法，利用温度传感器测量几个固定位置的温度值，从而建立起各个部分能耗之间的关系。

计算模型如下：

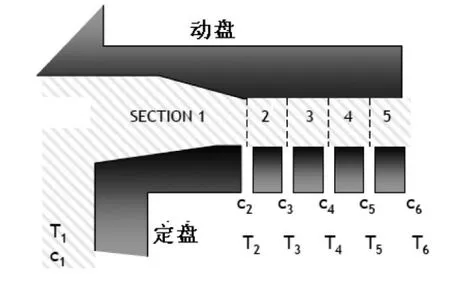
图1 磨盘分区示意图

假定纤维和水温度一致，计算公式如下：

式中：mi表示浆流；Wi表示水流；Si表示蒸汽流；Fi-i+1表示水和蒸汽之间的质量流量；Ci表示浆料浓度；Pi-i+1表示在i和i+1之间消耗的能耗，Hmi表示浆料热含量，Hwi表示水的热含量，Hsi表示蒸汽的热含量。

2.4 磨浆剪切和挤压功耗法

也有文献[8]研究磨浆的作用，将磨盘磨片对纤维的作用分为剪切和挤压的作用，磨浆区有效功率分为剪切和挤压功率之和，剪切功率计算式为：

其中：R磨盘平均半径；γ动定磨齿交叉角度；λ磨齿齿面面积占有率；α为动齿倾角；k为磨片内外径比；φ为摩擦力和动盘切向速度的夹角。

从上面挤压功率和剪切功率的计算式中，可以看出磨片齿形参数对磨浆功耗的影响。不同的磨浆阶段，磨浆质量要求不同，因此需要不一样的磨片齿形。对于低浓磨浆，主要是对纤维的切断作用，因此应尽量让剪切功率大一些；对于高浓磨浆，主要是对纤维的分丝、细化作用，因此尽量让挤压功率大一些。对于选择合理的齿形参数以保证磨浆质量和降低磨浆功耗具有重要指导意义。

2.5 其他计算方法

刘长恩，柳顺熙，付刚毅等[9]在文献中指出利用齿刃比负荷Bs、刀齿每秒切断长Ls，引导出磨浆有用功率，利用刀齿每秒切断长和磨片齿形参数之间的关系，可以计算出磨浆能耗。

O.Johansson等[10]在文献中提到，对单根纤维的运动分析建立功耗模型，计算了从纤维上剥除微纤维所需要的能量，求出这种能量大约为实际消耗能量的0.1%。普遍认为磨浆的效率是较低的，相当大的能量消散在纤维周围的水中，对有益的功没有贡献。对单根纤维的分析，具体情况完全是推理性的，还有待于实际检验。

Jan-Erik Berg[11]利用力学传感器来测定磨浆过程中浆料对磨齿的剪切力，来计算有效功率，表达式如下：

其中 Pr单位面积功率 ；n磨盘转速；τ(r)单位面积剪切力

R.J.KEREKES等[12]对低浓的研究在文献中指出平均每单位长度所受剪切力是挡坝运动方向施加的，所有这些力量乘以局部半径之和可以确定转矩从而估计功耗。

Adam Mroziński在文献[13]中通过对磨浆区纤维的磨浆作用将磨浆有效能耗分为四个部分：1)用于打浆的能耗 ；2)用于磨浆的效率；3)切断纤维消耗的能量；4)用于磨区摩擦消耗的能量。

3 基于摩擦力矩理论对不同磨浆浓度的有效能耗求法

3.1 低浓盘磨机摩擦力矩能耗求法

根据低浓（7%以下）打浆理论，纤维的摩擦作用相对较弱，计算有效能耗只考虑浆料的流变效应。如前面介绍的李世扬[4]在文献中提出的摩擦力矩方法得出的能耗计算公式。

3.2 中浓盘磨机摩擦力矩的能耗求法

叶列坤，李世扬[14]根据中浓（7%～15%）打浆理论，认为磨区内摩擦分为2种，一是磨盘与纤维之间的摩擦；二是纤维之间的摩擦。其中磨盘与纤维之间的摩擦能耗为：

式中：f1为磨盘与纤维间的摩擦系数；f2为纤维间的摩擦系数；K0为齿面占有率。

也有文献直接将摩擦系数分为2个部分进行求解，例如Atack and May[15]提出摩擦系数μ由纤维和磨盘之间的摩擦和纤维之间的摩擦系数之和来表示，但摩擦系数的取值还有待于研究。

3.3 高浓盘磨机摩擦力矩的能耗求法

李世杨[16]根据高浓打浆（15%～35%）理论将磨浆区功耗分为消耗在流态变化上的功率和消耗在物态变化上的功率，高浓磨区消耗的总功率P为这两部分功率之和。

由于高浓物料的流动性很差，常借助于螺旋的旋转运动将物料推至磨区入口处。物料离开螺旋时的线速度很低，进入磨区便获得很高的线速度，到达磨区外周时线速度最高。其中物料从磨区内向外围运动，速度变化所需的功率称为磨区流态变化功率Pv，其表达式为：

在高浓磨浆条件下，磨区中物料形态上的急剧变化，除了磨盘上磨齿的直接作用之外，主要是依赖于浆料之间相互剧烈的摩擦作用，Pm为磨区物态变化功率，其表达式为：

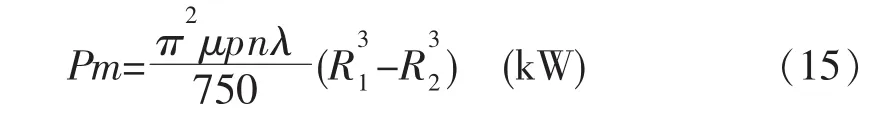
式中：Q含水物料通过量kg·s-1；g为重力加速度，m·s-2。

所以高浓磨区总功率P的数学表达式：

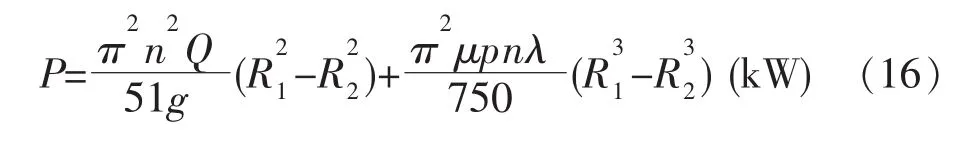
4 新型能耗模型

4.1 考虑磨盘间隙的借鉴算法（适用于高浓磨浆）

盘磨机磨浆区的摩擦力矩与液粘调速离合器摩擦类似，将盘磨机浆料考虑成粘度较大的粘液，基于液粘离合器摩擦力矩求法求盘磨机摩擦力矩功率[17]。结合前面介绍的油膜剪切摩擦机理，假设盘磨机磨浆区的浆料都是均匀的，磨浆时纤维在磨盘间隙形成浆层，磨盘通过对浆层的摩擦实现磨浆，磨区在磨浆过程中保持均压状态，与磨盘间隙变化无关。计算模型如下：

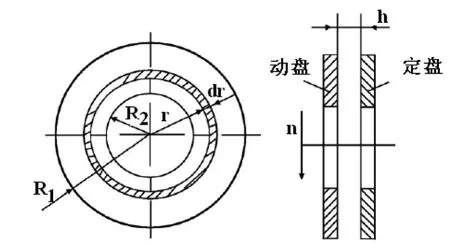
图2 模型示意图

在离磨盘接近表面上取微小圆环面dA=2πrdr，其浆料剪切应力 τ=2πnμr/h，剪切力 dF=τdA，传递的扭矩dT=rdF，对式进行积分可得磨盘摩擦面之间的扭矩为：

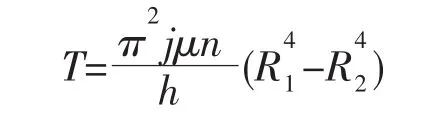
其中j=1、2单、双盘磨；h为磨盘间隙，m；克服这个扭矩需要消耗的功率为：

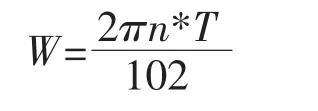
102—换算系数(1kW=102kg·m·s-1)。

所以磨浆区的消耗功率为：

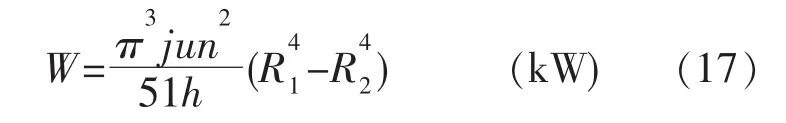
从式可见，扭矩与粘度、转速成正比，与磨盘间隙成反比，也符合实际情况。上述方法考虑到了磨盘间隙的作用，具体效果还有待于实践检验。

刘红峰，朱小林[18]在文献中对流量和进口压力的关系研究中发现，对于给定的浆种及磨片α、f、R1、R2、是确定的，磨区平均压强P也是定值。磨区的纸浆流量主要与磨片间隙及磨片半径有关，理论上在磨片的外径处Q最大，但计算盘磨机流量时一般取磨片的算术平均半径。指出磨区的纸浆流量Q和磨盘间隙与压力和流量之间的关系大致为：

将上述（18）式子代入式子（17）可以建立起磨片齿形和能耗之间的关系，具体效果还有待于实践检验。

4.2 对磨浆区能耗的估计算法

假设浆料悬浮液作为连续物被处理，那么它的性能就像固体或液体或者两者的混合物。磨盘对浆料通过滑动摩擦传递能量[19]。

（1）假设纤维悬浮液的性能像某种固体物料，则传给浆料的每单位质量的能量Ed可由下式求出：

式中：ω为磨片角速度；f为纤维对磨盘的摩擦系数；k为齿槽占有的面积；Q 为物质的流量（t·h-1）。

（2）假设把浆料视作某种纯液体进行处理，则传给浆料的每单位质量的能量Es可由下式求出：

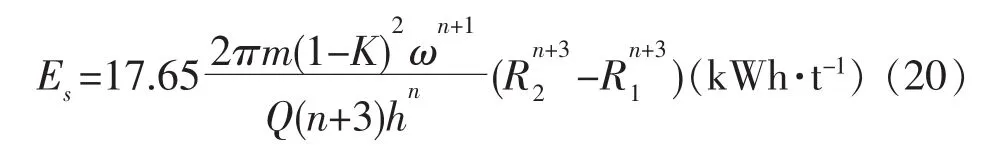
式中：m、n为流体特性系数；σ为磨盘间隙；17.65—换算系数(1马力·天=17.65kW·h)

实际上浆料是含有纤维固体和水分的悬浮物，能耗介于纯固体和纯液体之间。这种方法可作为盘磨机能耗的初步估算，应用于盘磨机粗略设计时，考虑基本参数对能耗的影响。

4.3 不同摩擦力矩模型对盘磨机磨浆功耗模型的影响

周培[20]在文献中对盘式离合器所能传递的摩擦力矩求法介绍了交大法，日本法，清华法三种计算方法。文献对三种算法取例计算分析、比较，认为交大法，清华法范围较为接近，适合国情，很多国内学者对盘磨机摩擦力矩的算法大多数借鉴第一种算法（交大法）。

5 结语

5.1 在对盘磨机能耗模型推导的过程中，习惯将磨区浆层简化为固体或流体，得到的多是未知变量较多的微分方程，不利于推广应用。本文所提出的方法，与一般计算方法相比，相对比较简单，公式中一些参数可以直接测量，简化了计算过程，缺点是对磨盘齿纹考虑较少，实际效果还有待于检验。

5.2 对于盘磨机摩擦力矩理论的推导，大都是建立在磨区压力P和摩擦系数u为常数这一前提下，而实际上由于温度等原因，黏度和摩擦系数都会不断变化。如何将这些参数的变化考虑到其中，还需要进一步研究。

5.3 从前面推导的能耗模型可知，改变磨盘磨纹可以改变参数CrCs，从而改变磨区有效能耗的大小。合理的磨区设计，可得到合适的节能的磨区结构，达到较大幅度降低能耗的目的。

[1]傅舟渔，沈潇，董宜臣等．煤矿液黏软启动装置摩擦片摩擦机理分析 [J]．煤矿机械，2013，34(05)：108-110．

[2]刘士亮，陈中豪．磨片齿宽对短纤维中浓磨浆成浆质量和磨浆能耗的影响[J]．中国造纸，2006，25(11)：9-12.

[3]刘靖.盘磨机主机功率消耗理论研究 [J].纸和造纸，2012，（31）5：16-18.

[4]李世扬.盘磨机动力消耗的计算与比较—降低盘磨机动力消耗的探讨之为 [J]．广东造纸，1983（1）：29-37.

[5]RouxJean-Claude,JorisGeorges.Angularparameters beyondspecificedgeload[J].PaperScience,2005.

[6]苏昭友，王平.盘磨机磨片的设计理论与方法[J]．纸和造纸，2011，30（8）：：10-15.

[7]Mirja Illikainen,Esko Harkonen,Jouko Niinimaki.Power consumption and fiber development in a TMP Refiner plate gap：comparison of LE-and standard refiner segments[J].Finland,2007.

[8]Georges Joris.The industrial refining process[J].Tappa,2005.

[9]刘长恩，柳顺熙，付刚毅等.盘磨机的功率和效率[J].黑龙江造纸，1995（1）：1-6.

[10]O.Johansson,M.Jackson,N.W.Wild.Three steps to improved TMP operating efficiency[C].InternationalMechanicalPulping Conference,2007.

[11]Jan-Erik Berg,Wood and fiber mechanics related to the mechanical pulping process[D].Mid Sweden University,2008.

[12]R.J.KEREKES,J.J.SENGER..Characterizing Refining Action in Low-Consistency Refiners by Forces on Fibers[J].Journal of pulp and paper science,2006,32(1)：1-8.

[13]Adam Mroziński.Modelling of waste-paper stock treatment process in disc refiner [J].Journal of POLISH CIMAC,2010(5)：113-119.

[14]叶列坤，李世扬.盘磨机中浓打浆耗数学模型的研究[J].广东造纸，1997（3）：24-27.

[15]Atack,D.and May,W.D.Frictional mechanisms in the grinding process[J].Pulp and Paper Magazine of Canada,1958：265-271.

[16]李世扬.高浓磨区能耗浅析 [J].轻工机械，1996（2）：16-19.

[17]吴超，郭刘洋.液粘离合器带排扭矩影响因素的试验[J].研究车辆与动力技术，2012（3）：40-42.

[18]刘红峰，朱小林．中浓盘磨机纸浆流量与进浆口压力关系的研究 [J].陕西科技大学学报，2010（28）：49-53.

[19]王绍析．对圆盘磨的理解—纤维的机械处理[J].造纸技术通讯，1979(02）：58-65.

[20]周培．盘式摩擦离合器摩擦力矩计算方法对比分析[J].陕西工学院学报，2004，20（4）：4-7.