基于协同机制与博弈策略的供应商选择研究
2013-12-29方忠民陈治亚曾明华
方忠民,陈治亚,曾明华
(1.湖南铁路科技职业技术学院,湖南 株洲 412000;2.中南大学 交通运输工程学院,湖南 长沙 410075;3.华东交通大学 交通学院,江西 南昌 330013)
基于协同机制与博弈策略的供应商选择研究
方忠民1,2,陈治亚2,曾明华3
(1.湖南铁路科技职业技术学院,湖南 株洲 412000;2.中南大学 交通运输工程学院,湖南 长沙 410075;3.华东交通大学 交通学院,江西 南昌 330013)
基于生产效率的波动性,构建了供应商作业协同程度的评价协同学模型,分析了模型的序参量;结合供应链博弈策略和协同机制,在生产效率一致时,为使得市场的资源配置更加有效,构建了供应链博弈策略模型,从供应商与需求企业的利润及社会福利的角度考察了供应商选择的博弈过程,提出了供应商选择方法模型和求解模型的算法。最后,通过算例仿真验证模型和算法的有效性。
供应商选择;协同机制;博弈策略;社会福利;遗传算法
随着生产专业化程度越来越高,企业越来越专注于自身的核心业务,很多零部件都从外部采购或者外包加工,这种制造模式要求企业与越来越多的供应商合作,使得供应商的评价与选择问题不断被赋予新的内涵,成为一项重要的研究课题,得到了学术界和企业界越来越多的关注[1-3]。
在生产效率一致时,不考虑无谓损失的情况下,通过确定价格水平可以增加供应商的生产剩余和需求企业的消费者剩余总和,即社会福利,使得市场的资源配置更加有效,因此从供应商与需求企业的利润及社会福利的角度来考察供应商选择的协同与博弈过程是十分必要的。
一、供应商协同机制模型
供应商的生产效率影响需求企业的生产效率和供应商的选择策略[4],同时,供应商的生产效率受到来自外部的供应商的竞争压力,表现在两个方面:其一,不同供应商的生产效率的竞争与协同作用,即在一定基础上促进了供应商生产效率的提高,同时又在需求企业的选择上处于相互竞争的地位;其二,供应商竞争策略的选择,即采用不同的价格体系,决定生产批量。
需求企业对某个产品的需求受到供应商体系的总体生产效率的影响[5],即社会平均生产时间的影响,不考虑替代产品的影响;由于社会平均生产效率是供应商生产效率的函数[6],因此,可以得出需求企业的生产效率实际受到供应商生产效率的影响。
1.生产效率不确定性的协同机制
在此我们设Qi为第i个供应商的生产批量;lt为需求企业给供应商的提前期,体现了时间柔性的特点;qi为第i个供应商的生产效率;εqi为供应商受其他因素影响产生的随机生产效率的值,服从正态分布 N(μqi,σqi);Eq
i为供应商与需求企业、供应商之间的关于其他生产效率和需求增长率的影响度函数;Dt+lt为需求企业在提前期到期时的需求量;εd为需求企业受其他因素影响产生的需求随机量,服从正态分布N(μD,σD);ED为需求企业受供应商生产效率的影响度函数。
根据哈肯协同机制[7-10]的原理,我们可以构建生产效率不确定性模型,如式(1)所示:

若考虑时间柔性的影响,则提前期的方程可以归纳为:

则基于生产效率不确定性的方程可以归纳为:

当采用需求拉动式生产时,提前期即时间柔性是序参量,根据相应的消元法可以求解方程;当采用推动式生产时,需考察供应商与企业在供应链中所处的位置,若供应商有较大的优势,则变量qi为序参量;若企业有较大的优势,则变量d为序参量;同样,使用绝热消元法可求解方程。
2.供应商作业协同评价模型
供应商作业协同度体现的是供应商的生产批量在提前期时间内最大的供应商与需求企业能力之间的协同程度,可用方程表示如下:

二、供应链博弈策略模型
在生产效率上,供应商的竞争促进了供应商能力的提高,提高了社会生产效率,体现了供应商之间长时期的竞争与协同形态转化过程,但是却未能体现短时期内供应商与需求企业之间的博弈过程。在选择供应商时,在生产效率较为一致的供应商之间存在着一定的博弈策略,供应商运用不同的博弈策略获得订单,从而为需求企业提供产品的需求与生产服务。此处我们假设供应商与需求企业之间的关系为完全信息扩展博弈[11],因此运用博弈论的方法来研究在供应商选择过程中的供应商竞争策略模型是可行的。
在生产效率一致时,根据微观经济学原理[12],在供给与需求确定的情况下,不考虑无谓损失的情况下,通过确定价格水平可以增加供应商的生产剩余和需求企业的消费者剩余总和,即社会福利,使得市场的资源配置更加有效,因此从供应商与需求企业的利润及社会福利的角度来考察供应商选择的博弈过程。
1. 供应链博弈策略模型
设供应商的原材料单位成本为pSi;制造与管理分摊成本为cSi,是关于生产批量的函数,生产批量越大,制造与管理分摊成本越小,随着生产批量的增加,企业负荷增大,制造和管理分摊成本反而增大;需求企业的制造与管理分摊成本为c,同理是关于生产批量的函数;材料的单位采购成本为p;需求企业的单位产品售价Pd;市场需求量为Q,是时间的函数;单位产品所需的原材料数量为e;需求企业的利润为B;供应商的利润为BSi;产生的社会福利为W。
在供应链博弈过程中,存在以下的博弈过程,其目标取值过程如下标所示:

表1 博弈过程福利函数取值表
由于供应商的生产效率不同,附加成本也会随着生产效率的变化而变化,因此,加入额外成本项cSi(Qi/t)来刺激供应商加快生产速度,提高生产效率。则有:

(1)若从供应链整体角度考虑社会福利,则有:

若要使得供应商的总生产剩余最大,转化为求解BSi对Q,pi的二元隐函数极值问题。此时pi为定值p0,可转化为条件极值问题:

此时,对于供应商有 pi≤p0,才能形成供应商的生产者剩余。解得BSi在驻点(p0,Q1)处取得极大值,此时需求企业的消费剩余为B(p0,Q1),则总社会福利为B(p0,Q1)+BSi(p0,Q1)。
(2)若要使得需求企业的消费剩余最大,转化为求解B对Q,p的二元隐函数极值问题:

此时,对于供应商有条件 pi≤p′0,才能形成需求企业的消费者剩余。
解得B在驻点(p′0,Q2)处取得极大值,此时需求企业的利润为BSi(p′0,Q2),社会福利为 B(p′0,Q2)+BSi(p′0,Q2)。(3)若要使得合作时产生最大的社会福利,则需转化为求解W对Q的二元隐函数极值问题:
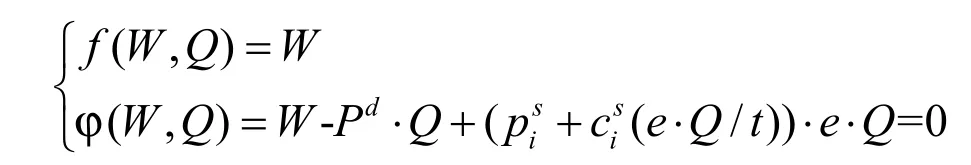
解得W在(p0,Q0)取得最大值W0。
在供应链中,应确保利益最大化,因此供应商与需求企业的利益之和所确定的供应链博弈策略模型为:
Bc=max[B(p0,Q1)+BSi(p0,Q1),B(p′0,Q2)+BSi(p′0,Q2),W0]
2.模型求解
供应商与需求企业合作时体现的博弈策略模型,以情况(3)为例,其求解过程如下所示:


三、供应商选择方法
供应商选择的方法着眼于考察供应商作业协同能力以及供应链社会福利值的大小。因此供应商选择时,可建立供应商选择多目标规划模型。由于供应商作业协同能力模型的取值范围为0<α≤1,因此我们运用乘数法即可有效的求解多目标规划模型。由于供应商合作水平层次不齐,在此我们规定作业协同能力α需大于最低标准值α0,对不符合要求的供应商直接淘汰,不在供应商选择多目标规划模型中求值。
(1)供应商选择多目标规划模型
综上所述,供应商选择多目标规划模型为:
Z=max(α·Bc)
(2)模型求解
步骤1:初始化数据;
步骤2:求解供应商作业协同能力,将供应商按照等级(0,0.1],(0.1,0.2],……,(0.9,1]划分十个级别,将低于α0的供应商淘汰,大于等于α0的供应商仍按不同等级存放在备选供应商集合中;
步骤3:求解供应链社会福利值;
步骤4:根据公式Z=max(α·Bc)求解最优目标值,即得到合格供应商;
步骤5:输出合格供应商,结束。
四、实例分析
在某机械设备产品制造过程中,在供应链中,有一个制造商,可供选择的供应商为10个。假设供应商生产额外成本函数为r·(lti+t)/Q,A产品制造商需要在10天内制造100单位的产品A,供应商的单价为20000,需要原材料B,其需求量为50。订单下达后供应商备料需要的时间为向量lt小时,lt={100,400,200,95,81,77,120,130,111,115},供应商的成本价为pSi=(20,16,35,15,16,24,15,26,27,22),成交单价设定为p0=30,每件原材料在A产品中的增值为ΔV=60。在此不考虑随机因素与提前期的影响,建立如下方程:

在此,我们假设制造商为主导企业,则序参量为d。
如图1所示,运用工具绘制两者(第一个供应商与制造商)对比的生产效率图。

图1 第一个供应商与制造商生产效率协同演化过程图
当制造商未选择合格的供应商时,供应商根据市场需求生产相应的产品,而市场的需求总是随着时间的变化而变化。因此根据博弈策略模型,我们可以给出方程组:
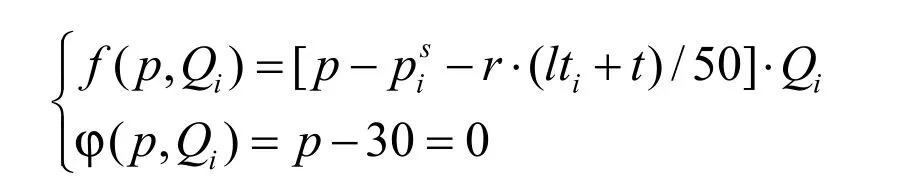
可见,方程组中第一个方程式为关于时间的隐函数。从而我们可以求得在供应商的生产者剩余与时间的变化关系。我们可以得到社会福利与生产时间的关系图如下图2所示,
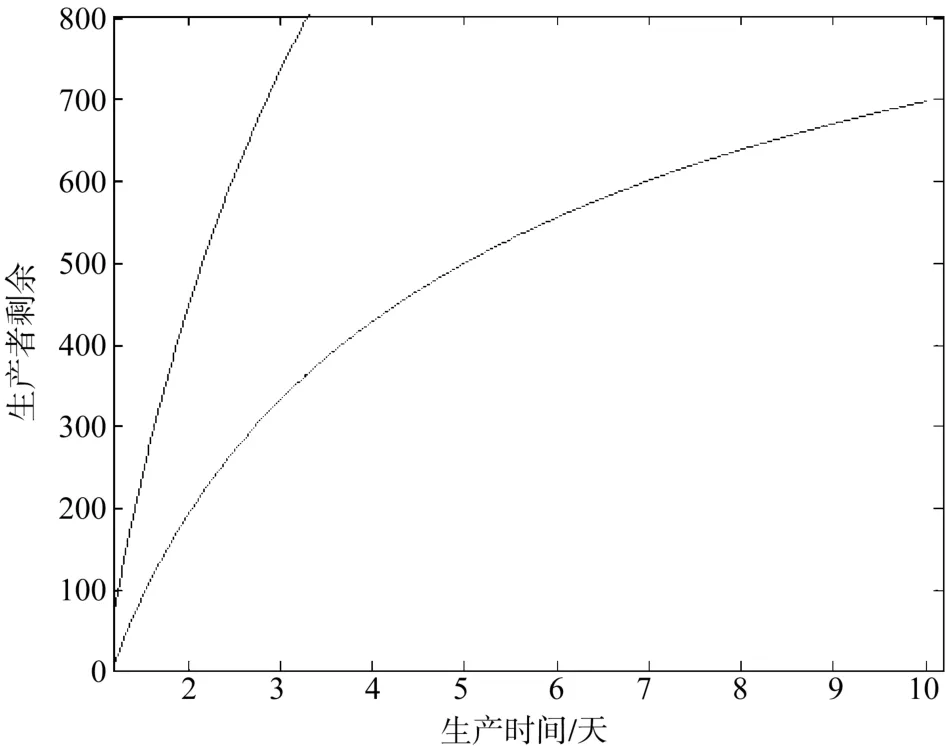
图2 选择不同供应商时生产者剩余与生产时间的变化关系
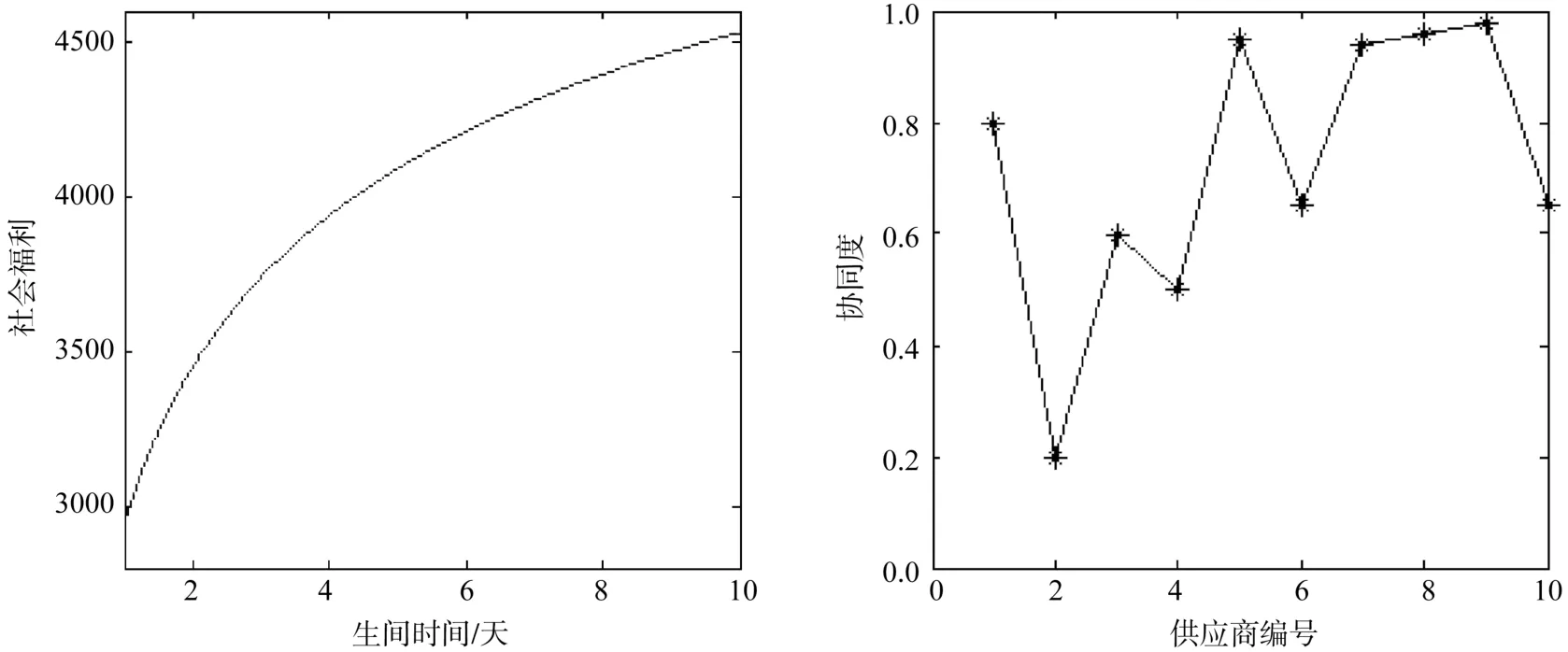
图3 供应商选择分析图
最终,经过计算我们选择第5个供应商为合格供应商,此时社会福利为4580,协同度为0.95,如图3所示。
[1] 贾俊秀. 2-2供应链网络下生产能力和定价策略研究[J].计算机集成制造系统,2008,14(10):2036-2045.
[2] Qian Li. An ANN pruning algorithm based approach to vendor selection[J].Journal of Systems Management (USA), 1995,46(5):314-320.
[3] 邹 敏,杨光华. 湖南省产业结构对物流需求的影响研究[J]. 中南林业科技大学学报(社会科学版),2012, (1):30-32.
[4] 蒋琦玮. 不确定环境下供应商选择优化方法研究[D].中南大学博士论文,2011.
[5] 朱建军,刘士新,王梦光,等. 供应商选择及定购计划的分析[J]. 东北大学学报(自然科学版),2003,24(10):956-958
[6] 符 瑛,王立新. 长株潭区域物流需求预测因素分析[J]. 中南林业科技大学学报(社会科学版),2012, (2):62-64.
[7] H. Haken. Advanced synergetics [M]. Berlin: Springer-verl etc, 1987.
[8] Haken Hermann. Synergetics: An introduction [M]. Berlin: Springer,1983, 3rd.
[9] H. Haken. Information and self-organization: a macroscopic approach to complex systems[M]. Berlin Germany: Springer, 2006.
[10] Haken, H. Cooperative phenomena in system far from thermal equilibrium and in nonphysical systems [J]. Rev. Mod. Phys. 1975,(47): 67-121.
[11] 马丁J.奥斯本, 阿里尔·鲁宾斯坦. 博弈论教程[M]. 北京:中国社会科学出版社,2000.
[12] 曼 昆. 经济学原理(第五版)微观经济学分册[M]. 北京:北京大学出版社,2009.
A Study of Supplier Selection Based on the Collaborative Mechanism and Game Strategies
FANG Zhong-min1,2, CHEN Zhi-ya2, ZENG Ming-hua3
(1. Hunan Railway College of Science and Technology, Zhuzhou, 412000,Hunan, China; 2. School of Traff i c, Transportation, Central South University,Changsha 410075, Hunan, China; 3. School of Transportation, East China Jiao Tong University, Nanchang 330013, Jiangxi, China)
Based on the fluctuation of production efficiency, the study constructs an evaluating synergetic model of the supplier collaboration degree, and analyzes the sequence participation amount of the model; combined with the game strategy and collaborative mechanism of supply chain, it puts forward the model of supplier selection and the algorithm of solving the model when production eff i ciency is consistent, building a supply chain game strategy model to investigate the game process of supplier selection from the prof i t and social welfare of the supplier and the demand in order to make the allocation of the market resources more effectively. In the end, the eff i ciency of the model and algorithm is validated by a case simulation.
supplier selection; collaborative mechanism; game strategy; social welfare; Genetic Algorithms
F713.3
A
1673-9272(2013)01-0047-04
2012-11-06
湖南省哲学社会科学基金资助项目:“基于时变需求的供应商协同分析研究 ”(编号:2010YBB246);湖南省自然科学基金项目“基于时变需求和时滞的供应链系统控制问题研究”(编号:09JJ3135);江西省教育厅科技计划项目“可持续发展的城市交通网络结构优化研究”(编号:GJJ12322)。
方忠民(1968-),男,湖南湘潭人,湖南铁路科技职业技术学院副教授,中南大学交通运输工程学院博士研究生,研究方向:供应链管理。
陈治亚(1958-),男,湖南岳阳人,西安电子科技大学教授,博士生导师,研究方向:交通运输经济研究和交通运输企业管理。
[本文编校:杨 灿]
