变形监测数据处理方法改进

陈云兰 郑周勇

(重庆市国土资源和房屋勘测规划院，重庆 400050)

1 概论

测量机器人有自动目标识别、自动照准、自动测角与测距、自动目标跟踪、自动记录等优点，所以被广泛地应用于测绘领域，特别是在变形监测项目中的应用，在一定程度上实现了监测自动化和一体化。目前，基于测量机器人的自动变形监测系统大多是单测站的测量系统，而且数据处理模式是在假设测站点稳定的情况下进行的，当变形范围较大时，要保证测站点是稳定的，势必增大测站点与观测点之间的距离，降低测量的精度。为了提高观测点的精度，可把测站点设在变形体上，这时必须考虑测站本身的变形问题。于胜文等［1］人提出了应用坐标转换的思想消除测站点变形对变形量的影响。

同时，由于变形监测重复性的特点，定期要对基准点和观测点进行观测，而每次观测都存在测量误差。以往的监测数据处理方法是假设每周期的基准点没有误差，以基准点作为已知点进行平差处理。

由于上述处理方法不严密，利用坐标转换思想处理变形监测数据的可行性在文献［1］中已经得到了证实，整体最小二乘法在数据处理上的优越性已经得到广泛认可［2-4］。本文在文献［1］的基础上，结合整体最小二乘法可以同时顾及两套坐标系误差的优点和任意旋转角度坐标转换无线性化误差的特点，提出利用基于整体最小二乘法的任意旋转角度三维坐标转换模型处理变形监测数据。

2 工作基点变形和基准点测量误差的数据处理模型

2.1 任意网平差处理

将第二周期及以后外业采集回来的数据(水平角观测值、距离观测值)编辑成所用平差软件要求的输入文件格式，运用任意网平差方法进行平差。本文采用的是范东明［5］开发的任意平面网平差处理软件(NET3.0)和水准网平差处理软件(LEVEL3.0)进行平差处理。

平面网平差步骤如下:

(1)把观测数据整理成水平角观测文件(ANG.DAT)和距离观测文件(DST.DAT)。除了2个观测文件外，本软件还需要3个已知文件:方位角文件(AZM.DAT，可以为空文件)、点坐标文件(CST.DAT)以及图例文件(FIG.DAT，一般情况下为空文件，只有在网形不收敛必须借助图形时才用);

(2)假设任意一观测方向的方位角为某个值，把他按格式填入到AZM.DAT文件;再给任意一个已知点的坐标赋值，按格式写入CST.DAT文件;

(3)准备好以上5个DAT文件后，开始平差，得到坐标平差值及单位权中误差μ。

水准网平差步骤如下:

(1)编辑高差观测文件(LEVEL.DAT);

(2)准备已知高程文件(ADJ.TXT);

(3)启动水准网平差软件，开始平差，得到观测点的高程，把它作为Z坐标值。

2.2 基于整体最小二乘法的任意旋转角度三维坐标转换处理

通过平面网平差和水准网平差，可得到基准点和观测点每周期的三维坐标平差值。但是每个测量周期都是以测站点为坐标原点，以过仪器中心的铅垂线为Z轴，X轴指向某一基准点，Y轴与XZ平面正交，建立一个独立的空间直角坐标系统。所以每个测量周期的坐标值分属不同的坐标系统，不能直接进行比较，需要进行坐标转换之后再作对比。

假设首期的基准点坐标和测站点坐标为［X1Y1Z1］T，首期之后各期基准点坐标和测站点坐标为［X2Y2Z2］T，以它们为控制点，利用布尔沙(Bursa)转换模型求解坐标转换参数。转换模型为:

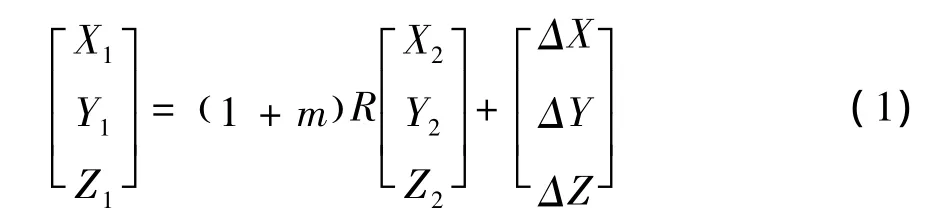
式中:m— 尺度因子;［ΔX ΔY ΔZ］T— 平移参数。

设两坐标系间的旋转角(欧拉角)为 εX，εY，εZ，则

由文献［6］可知，平移参数与旋转和缩放参数的组合有线性关系，在公共点较少区域范围较小的情况下，可将2套坐标系的坐标重心化，将平移参数跟旋转参数和尺度因子分开求。一般变形监测网的区域都不是太大，完全可以先重心化，再求解除平移参数以外的其他转换参数。且令m0=(1+m)，

则式(1)可改写成:

式中:［X'1(i)Y'1(i)Z'1(i)］— 第i个控制点在首期独立坐标系下重心化后的坐标;［X'2(i)Y'2(i)Z'2(i)］—第i个控制点在首期之后各期独立坐标系下重心化后的坐标。采用文献［7］的迭代方法求解，步骤如下:

(1)N(0)=0，x(1)=(ATA)-1ATY(2)迭代

及参数精度:

式中:tr—取矩阵迹算子;vec— 矩阵列向量化算子;⊗— kronecker积算子。进一步得出本文处理方法的精度为:

解出转换参数后，可将首期之后每期观测点的坐标转换到首期坐标系统下，随即可得各观测点在2个周期观测时刻的坐标差，即为变形值:

3 实际工程数据计算与分析

为了验证本文方法的有效性及合理性，选取一个变形监测项目所有基准点(J1、J2、J3)和一个变形监测点(A01)连续10期的监测数据(表1、表2)，分别用直接平差处理法(把测站点和基准点首期坐标作为已知数据，分别进行平面网和水准网平差)、基于最小二乘法的坐标转换法及本文处理方法计算某一变形监测点的变形量及精度。

表1 水平角观测值

表2 水平距离和高差观测值

每测量周期观测得到的基准点的数据是有差别的，特别是水平角观测值，最大值和最小值相差1'之多。把他们之间的不等归结于测站点变形和基准点测量误差。

用3种处理方法对表1和表2中的数据进行处理，分别得到了各自的转换精度，结果见图1～图3。

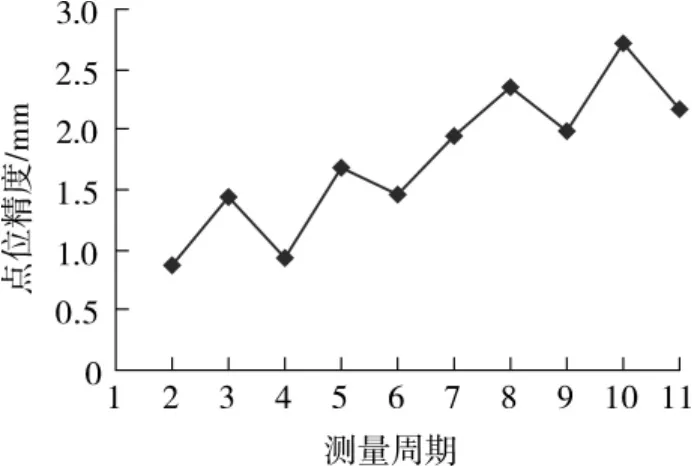
图1 直接平差法点位精度

图2 基于最小二乘法的坐标转换模型的点位精度

图3 基于整体最小二乘法的坐标转换模型的点位精度

在不顾及测站点变形和基准点误差的情况下，得到的观测点的点位精度较差，而且随着测量期数的增加，点位精度有增大的趋势;用基于最小二乘法的坐标转换模型处理时，只顾及了测站点变形的影响，观测点的点位精度高了很多，基本上都在1 mm以内;基于整体最小二乘法的坐标转换模型处理得到的精度最高，基本可以控制在0.5 mm以内。不顾及测站点变形对变形量的影响较大，考虑测站点的变形可以大大提高监测结果的精度，同时考虑测站点的变形和基准点的误差精度更高，结果更可靠，理论更严密。

4 结论

当测站点离变形体较近或在变形体上时，必须考虑测站点自身变形对变形点的影响，本文利用坐标转换的技术消除或消弱了测站点自身变形对观测点变形量的影响;测量误差不可避免，但可以减弱它对结果的影响，利用整体最小二乘法坐标转换模型来处理变形监测数据，同时顾及两套坐标系下控制点的误差，消弱测量误差对变形监测结果的影响，使监测结果更可靠。

［1］于胜文，王静，孙为晨.顾及测站点变形的数据处理方法［J］.山东科技大学学报:自然科学版，2009，28(2):8-12.

［2］魏木生.广义最小二乘问题的理论和计算［M］.北京:科学出版社，2006.

［3］陆珏，陈义，郑波.总体最小二乘方法在坐标转换中的应用［J］.大地测量与地球动力学，2008，28(5):77-81.

［4］孔建，姚宜斌，吴寒.整体最小二乘的迭代解法［J］.武汉大学学报:信息科学版，2010，35(6):711-714.

［5］范东明.任意平面网坐标自动解算的非线性最小二乘平差算法［J］.铁道学报，2002，24(4):78-82.

［6］杜兰，张捍卫，周庆勇，等.坐标转换参数之间的相关性解析［J］.大地测量与地球动力学，2011，31(1):59-62.

［7］Schaffrin B，Felus Y A.On the Multivariate Total Least Squares Approach to Empirical Coordinate Transformation［J］.J Geodes，2008，82(6):373-383.