一种高超声速飞行器的再入鲁棒输出反馈控制
2013-12-25张军,王玫
张 军,王 玫
(1.江苏大学 电气信息工程学院,江苏 镇江212013;2.上海机电工程研究所,上海200233)
滑翔返回的高超声速飞行器的飞行高度和飞行马赫数跨度范围大,运行环境非常复杂,飞行过程中飞行器气热特性和气动特性变化剧烈。动力学模型存在快时变、强非线性耦合、不确定性、多干扰等特性。采用传统PID增益调度控制很难适应大包络、多任务模式飞行运动[1]。因此,国内外研究者将非线性控制和鲁棒控制应用到控制器设计中,使得飞行器具有稳定的飞行特性和强鲁棒性能。
为提高控制系统的鲁棒性,H∞控制、μ分析、LPV控制、Backstepping控制、反馈线性化等方法被应用到再入控制中。文献[2-3]基于纵向动力学的线性化模型,采用H∞控制和μ分析方法提高抑制干扰的能力,改善了控制系统的鲁棒性。文献[4]采用LPV(线性参数时变)技术对复杂的非线性再入动力学模糊建模,使用LMI(线性矩阵不等式)工具和Lyapunov稳定理论设计LPV控制器。上述方法对再入动力学特性进行了较大的线性简化,未能从根本上进一步提高再入系统的控制效果。文献[5]利用时标分离原理设计动态逆解耦控制律,这种内外环近似分离使得控制模型精度受到影响。文献[6]采用反馈线性化对X-38动力学解耦,基于线性预测控制律设计飞控系统,但没有考虑模型的不确定性。文献[7]采用鲁棒反馈线性化方法对高超声速飞行器巡航段的非线性耦合模型解耦,设计最小最大鲁棒控制方法,但是计算比较复杂。
针对强耦合、非线性、不确定性的X-38再入动力学模型,采用鲁棒反馈线性化技术解耦,建立了范数有界的不确定线性系统;对解耦后的不确定系统设计动态高增益观测器,重构系统的不可观测状态,有效处理系统的非线性项和不确定性;设计自适应非光滑输出反馈控制器,实现状态的设定精度跟踪,避免了不确定边界的估算。最后,通过仿真验证了所提算法的有效性。
1 模型描述
考虑不确定X-38的再入无动力模型为
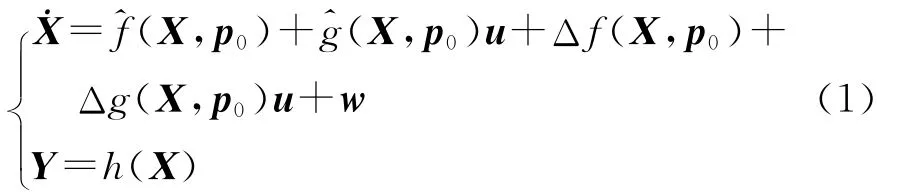
式中:X=(ωpωqωrαβσ)T,ωp,ωq,ωr分别为飞行器的滚动角速度、俯仰角速度、偏航角速度,α,β,σ分别为飞行器的攻角、侧滑角、速度倾斜角;p0为名义系统参数;Y=(αβσ)T;w为有界的力矩干扰为再入动力学的非线性标称函数;Δf,Δg为再入动力学中的不确定函数;h为输出函数。这里定义X-38标称模型为
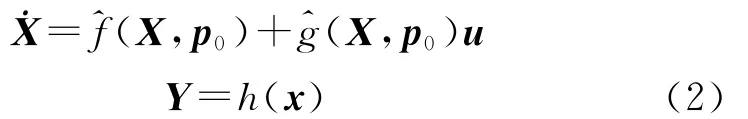
控制输入u为反作用控制系统(RCS)和气动舵面联合提供,X-38的再入段分为5个阶段,不同的飞行阶段有不同的控制结构(这里下标表示飞行阶段)。
在1和2飞行阶段,控制结构为RCS,有:
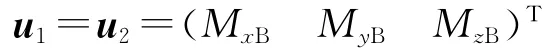
式中:MxB,MyB,MzB分别为 RCS提供的飞行器在x,y,z轴上的控制力矩。
在3飞行阶段,控制结构为气动舵面和RCS联合,有u3=(δeδaMzB)T。
在4飞行阶段为气动舵面,u4=(δeδa)T。
在5飞行阶段为气动舵面,u5=(δeδaδr)T,δe,δa,δr分别为左、右升降副翼和方向舵3个舵面的偏转角。在不同的飞行阶段动力学模型分别为

式中:I为惯量矩阵系数的组合表达式,C为气动力矩系数的组合,具体定义见文献[6],这里省略。从式(1)可以看出,高超声速飞行器姿态动力学模型是时变的非线性系统,并且与轨道参数耦合。
再入系数模型(1)的不确定性主要集中在动力学模型中的I,C系数中,因而输入矩阵不确定性满足|Δg(X,p0)|=|Δ|≤D,参数不确定性满足|Δf(X,p0)|≤fm,Δ为不确定矩阵,D和fm为不确定边界。
2 鲁棒反馈线性化
由于系统(1)是轨道参数和动力学参数强耦合的非线性系统,直接设计非线性控制律比较复杂,这里将其转化为线性系统。反馈线性化变换定义为
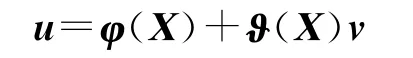
式中:φ(X),ϑ(X)为非线性变换函数,满足下面关系式:
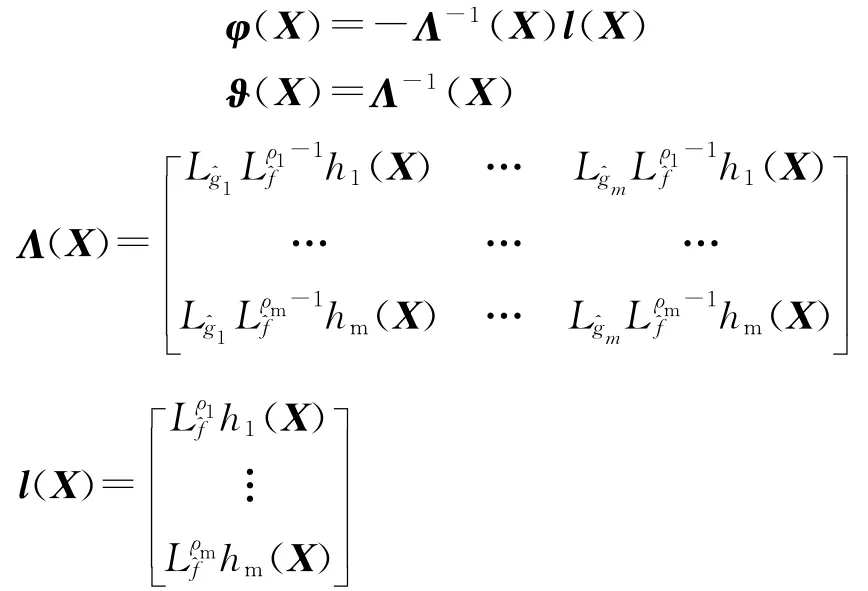
式中:L为李导数ρ为相对阶。
定义 新的变量z= ()T,h(X)=(αβσ)T,v为解耦后新的输入。对不确定非线性系统的反馈线性化:
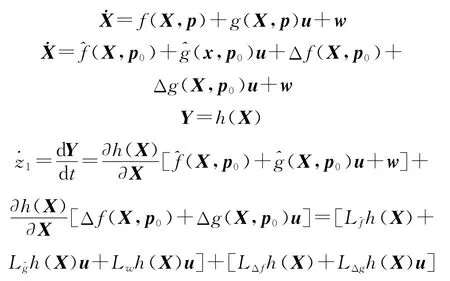
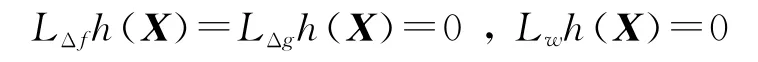
再入飞行阶段1,2,3,5的动力学模型相对阶为ρ=6,而飞行阶段4的动力学模型相对阶为ρ=4[8],应重新定义输出,使得系统能控。因此Lgh(X)=0,令
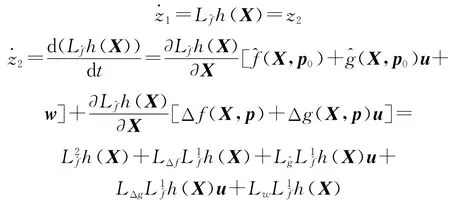
因此,反馈线性化后的模型为
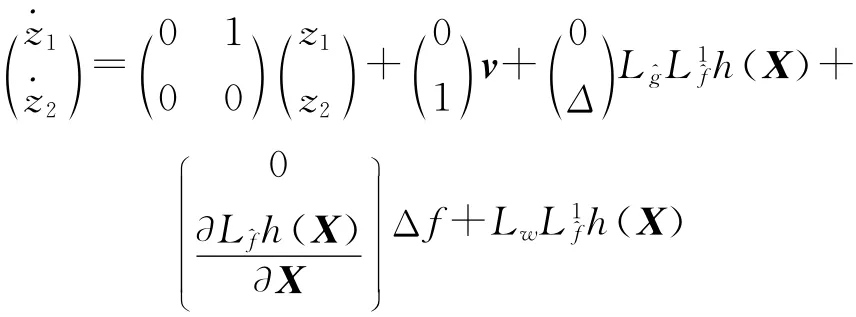
令z=(z1z2)T,由于Δ≤D,Δf≤fm,w≤wm,所以
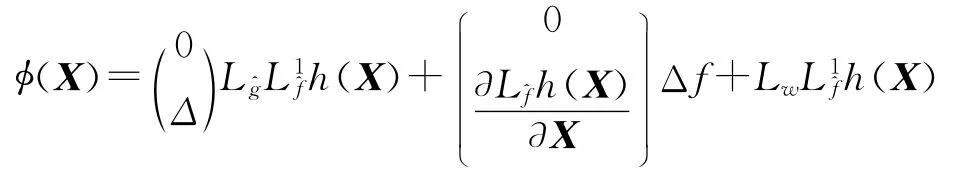
是状态相关的有界不确定项,反馈线化后的解耦系统等价为下面的范数有界不确定形式:
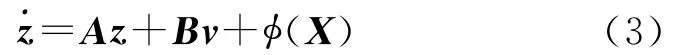
3 全局自适应输出反馈控制
解耦后的不确定系统(3)可写成为
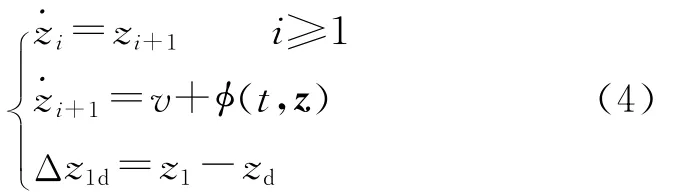
式中:|φ(t,z)|≤θ(|z1|+…+|zi|)+θ1,Δz1d为跟踪误差,zd为跟踪期望信号且连续可微,并且存在未知常数M≥0,使得supt≥0(|zd(t)|+|d(t)|)≤M,sup为上确界。本节引入动态高增益观测器重构系统(4)的不可观测状态,处理系统的非线性项和不确定性φ(t,z),不需要精确估计边界,避免鲁棒控制中通过复杂的计算估计不确定边界。设计步骤如下[9]。
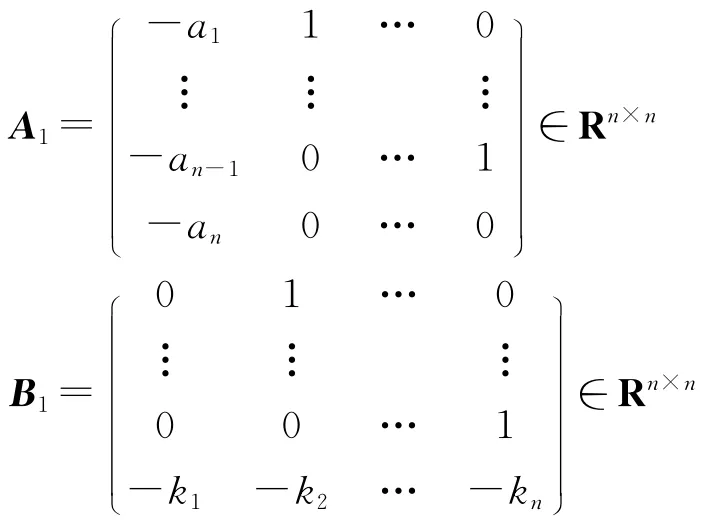
①选择设计参数ai>0,k>0,i=1,2,…,n,使得矩阵A1,B1是 Hurwitz的,且存在P=PT>0,Q=QT>0,满足:

式中:G=diag(1,2,…,n)。
②构造高增益自适应观测器和自适应非光滑输出反馈控制器:
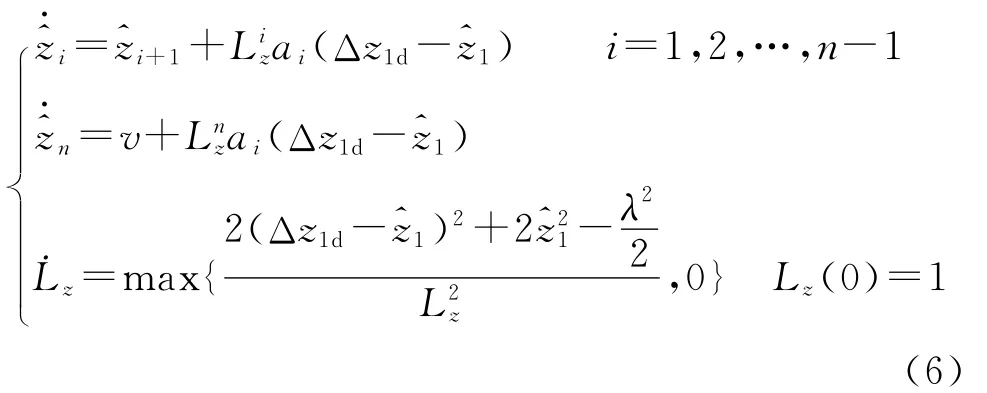
为zi的观测量,λ为跟踪精度,初始值
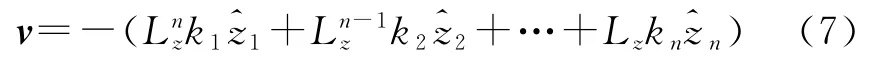
定理1 对于系统(4),基于动态高增益观测器的输出反馈控制器使得对于任意初始条件,闭环系统的解在[0,+∞)上有定义且有界,并且可实现全局设定精度的跟踪。
再入的过程中对输入和状态十分严格,因此自适应因子需要限制。将输入‖u‖≤umax转化为‖v‖≤vmax,这里对Lz增益的变化率进行限制,即z有约束,这里采用标量优化γ间接约束z,减少计算时间。由矩阵和向量范数相容性,得到:

由于0≤γ≤1,所以保证了闭环系统的稳定。此外,为了减少过渡时间,需要注意k2的选择。文献[9]的k2=1时,倾斜角跟踪曲线虽然收敛,但是过渡时间过长,不满足再入响应时间要求,这里k2=6。
4 仿真研究
飞行器模型和气动参数来自文献[6],仿真条件初值为α0=5°,β0=3°,σ0=5°。期望值为αe=0°,βe=0°,σe=0°。仿真周期10ms。分别将气动力矩参数和惯量系数拉偏10%,常值力矩干扰为10kN·m。最终摄动、偏差和干扰按照如下方式加入仿真:
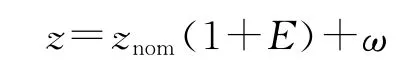
式中:znom为标称值,E为偏差,ω为零均值白噪声。图1~图4仿真结果显示攻角、舵机偏角δ、侧滑角、倾斜角在不确定性和干扰作用下的跟踪曲线,满足动态和稳态精度要求。
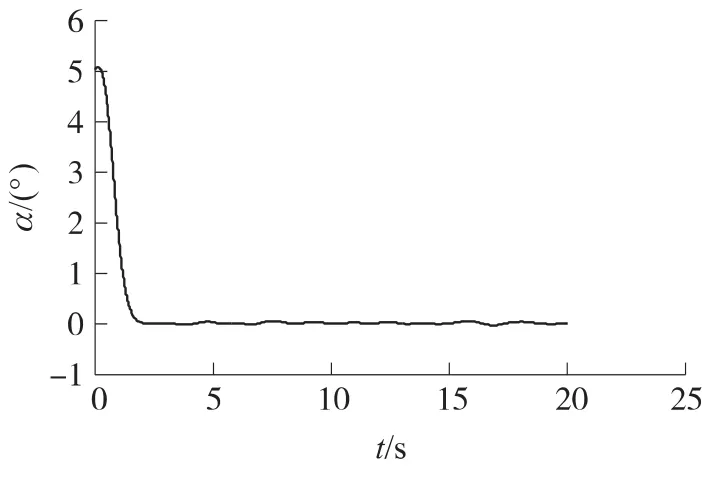
图1 攻角跟踪曲线
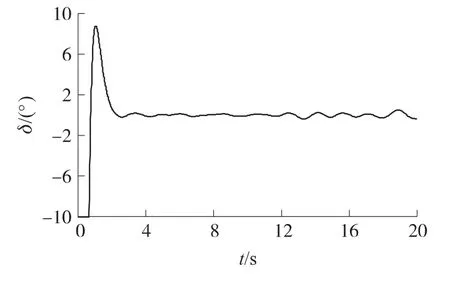
图2 控制输入曲线
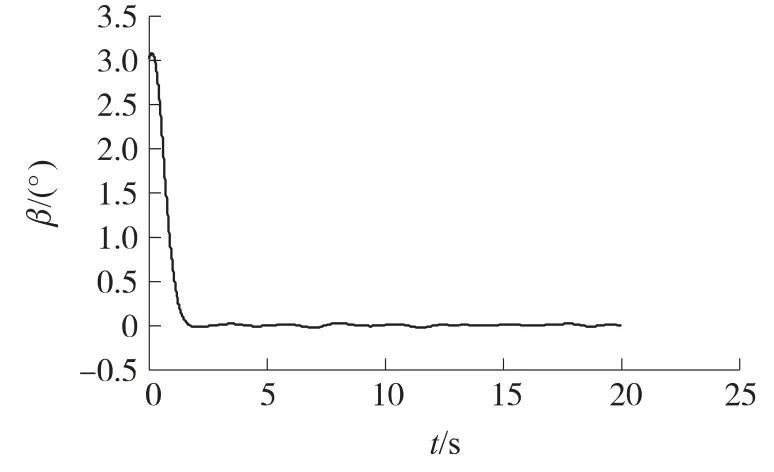
图3 侧滑角跟踪曲线
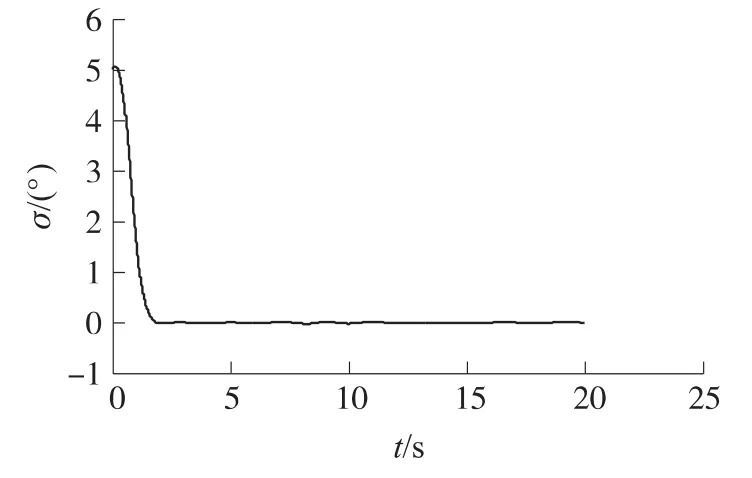
图4 倾斜角跟踪曲线
5 结束语
高超声速飞行器的再入段存在强耦合、非线性、不确定性等特性.本文提出鲁棒反馈线性化技术进行非线性解耦,建立了范数有界的不确定线性系统,降低了强非线性系统设计的难度。对解耦后的不确定系统,设计动态高增益观测器重构系统的不可观测状态,有效处理了系统的非线性项和不确定性。设计非光滑反馈控制器,实现状态的设定精度跟踪,通过仿真验证了所提算法的有效性。
[1]HARPOLD J.Shuttle entry guidance[J].Journal of Astronautical Sciences,1979,28(3):239-268.
[2]HIRET A.Linear-parameter-varying/loop-shapingH∞synthesis for a missile autopilot[J].Journal of Guidance,Control,and Dynamics,2001,24(5):879-886.
[3]尉建利,于运峰,闫杰.高超声速飞行器的鲁棒控制方法研究[J].宇航学报,2008,29(5):1 526-1 530.WEI Jian-li,YU Yun-feng,YAN Jie.Research on robust control of hypersonic vehicle[J].Journal of Astronautics,2008,29(5):1 526-1 530.(in Chinese)
[4]FUJIMORI A,TERYI F.Flight control design of unmanned space vehicle using gain scheduling[J].Journal of Guidance,Control,and Dynamics,2005,28(1):96-105.
[5]YURI B S,CHARLES E H.Reusable launch vehicle control in multiple-time scale sliding modes[J].Journal of Guidance,Control,and Dynamics,2000,23(6):1 013-1 020.
[6]VAN W R.Combined feedback linearization and constrained model predictive control for entry flight[J].Journal of Guidance,Control,and Dynamics,2006,29(2):427-434.
[7]REHMAN O U,FIDAN B,PETERSEN I R.Robust minimax optimal control of nonlinear uncertain systems using feedback linearization with application to hypersonic flight vehicles[C]//Proceedings of the 48th IEEE Conference on Decision and Control.Shanghai:IEEE,2009:720-726.
[8]XU Yun-jun.Multi-timescale nonlinear robust control for a miniature helicopter[J].IEEE Transactions on Aerospace and Elelctronic Systems,2010,46(2):656-669.
[9]闫雪华,刘允刚.一类具有未知增长率非线性系统全局输出反馈实际跟踪[J].中国科学:信息科学,2011,41(6):704-716.YAN Xue-hua,LIU Yun-gang.Global practical tracking by output-feedback for nonlinear systems with unknown growth rate[J].China Science:Information Science,2011,41(6):704-716.(in Chinese)
