临近空间高超声速飞行器DG-VSMM跟踪算法
2013-12-25李志淮谭贤四
肖 松,李志淮,谭贤四,王 红
(空军预警学院1.研究生管理大队;2.二系,武汉430019)
临近空间高超声速飞行器是指在距离地面20~100km的空域,飞行马赫数达到5以上的飞行器。近年来,临近空间高超声速飞行器的政治、经济和军事价值引起了各国的高度重视,并成为美国等军事强国的研究热点[1-2]。
目前,对常规机动目标跟踪的研究已经很成熟,但是,对临近空间高超声速目标跟踪的研究还处于起步阶段[3]。临近空间高超声速飞行器不同于传统的弹道导弹和常规飞行器,其飞行速度极快,飞行轨迹多变,运动特征多样,对跟踪系统提出了严峻挑战[4]。单模型跟踪算法难以准确描述目标运动状态[5];固 定 结 构 多 模 型 (Fixed Structure Multiple Model,FSMM)跟踪算法为了达到好的跟踪效果,必须使用一个大的模型集合,这就增加了计算的复杂性,而且过多模型间的不必要竞争反而会使性能下降[6];VSMM跟踪算法将能够描述目标主要机动形式的模型组成一个大的模型集合,在目标进行机动运动时,通过模型集合自适应(Model Set Adaptation,MSA)选择与目标机动形式最接近的模型子集来进行滤波计算,解决了FSMM跟踪算法中模型集固定和计算量大的问题,受到广泛青睐[7]。临近空间高超声速飞行器的运动状态可能在很短时间内发生较大变化,如果VSMM跟踪算法中的模型集自适应速度跟不上飞行器运动状态的变化速度,就会出现误差增大甚至跟踪失败的现象。鉴于此,本文选择目标可能的机动模型集合,设计模型之间的连通和转换关系,通过后验概率的大小来实时调整模型集,实现变结构跟踪。
1 问题描述
1.1 临近空间高超声速目标特性
自20世纪50年代以来,美国等国家经过多年不懈努力,制定出多项高超声速飞行器发展计划,并进行了多次地面和飞行试验。综合分析已经公布的相关信息[1,3],得到临近空间高超声速飞行器的目标特性:飞行马赫数为5~25,飞行高度为20~100km,机动过载能力为2g~10g,雷达反射面积为0.3~0.01m2,几何尺寸为1~20m,质量为0.5~5t。
临近空间高超声速飞行器是典型的“高、快、小”目标,更重要的是,临近空间高超声速飞行器的典型发射方式有机载发射、火箭发射和空间平台发射,其飞行轨迹不同于弹道导弹,可以周期跳跃飞行,机动灵活多变,给探测跟踪和拦截系统等提出了严峻挑战。
1.2 传统VSMM跟踪算法存在的问题
考虑如下随机混合系统:
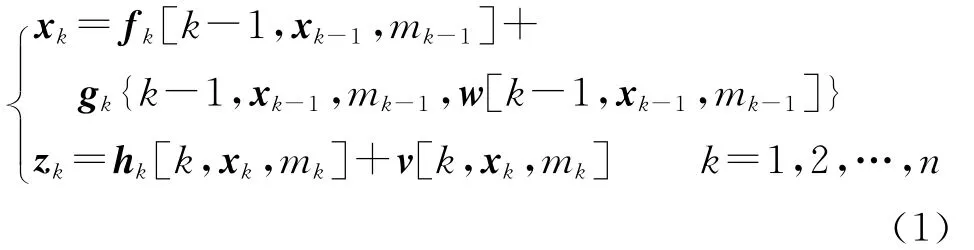
式中:fk[·]、gk[·]和hk[·]都是非线性函数,xk和zk分别为系统状态向量和量测向量,w[·]和v[·]分别为系统过程噪声和量测噪声,其协方差分别为Qk和Rk,mk为k时刻的系统模式状态,且mk⊂M,M为系统所有模型的集合。目标当前可能的模式与其前一时刻的状态(包括动力状态和模式状态)是相关的,即:
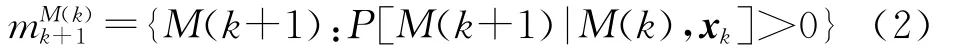
式中:M(k)为k时刻模型子集中的一个模型为相对于M(k)的下一时刻目标可行的模式集合,P[M(k+1)|M(k),xk]为与目标状态相关的模型转移概率。k+1时刻可行的模式集合应为
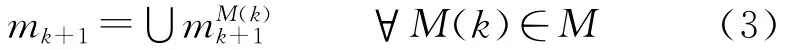
最小均方误差意义下的变结构多模型估计算法具有2层结构,高层为模式状态mk的估计,即MSA,是VSMM算法有别于传统算法的独特之处;低层为模型序列M(k)的估计,即多模型交互计算,与传统FSMM算法相同。自VSMM跟踪算法提出以来,有3种典型MSA算法:模型群组切换算法(Model Group Switching,MGS)[8]、自适应网格算法(Adaptive Grid,AG)[7]和可能模型集算法(Likely Model Set,LMS)[9]。MGS算法采用硬判决的模型集切换,容易导致误切换,这在临近空间高超声速飞行器的跟踪过程中容易导致跟踪丢失,增大了跟踪失败的风险;AG算法在滤波过程中根据上一时刻的估计结果建立新的模型并自适应调整模型间的距离,自适应产生新的、更为匹配当前机动的模型集合,虽然无须预先设定模型,但是通常先设置模型间距较为粗糙的模型集,在跟踪状态变化较快的临近空间高超声速飞行器时,算法一直处于模型间距较粗糙的模型集状态,从而导致跟踪误差较大;LMS算法的实质是主动图(AD)模型集自适应策略的具体实现,虽然比MGS算法的运算量要小,比AG算法的通用性要强,但是由于LMS算法只能激活主导模型的强邻模型,导致算法模型集的调整速度跟不上目标的状态变化速度,从而出现误差增大或者跟踪失败的现象。
2 DG-VSMM跟踪算法
鉴于传统VSMM跟踪算法的优点和存在的不足,本文选择的模型能有效覆盖临近空间高超声速飞行器的可能机动情况,根据模型之间的连通关系和转换概率建立模型有向图,使每一时刻起作用的模型子集根据目标的机动变化而变化。算法过程主要有选择模型集合、建立模型有向图和滤波计算3个步骤。
2.1 选择模型集合
假设临近空间高超声速飞行器在X-Y平面内运动,平面内的机动行为可以归结为速度和航向的变化。其中速度的变化可以用加速度a来表征,而航向的变化则由角速度ω来表征,临近空间高超声速飞行器也有可能进行匀速巡航,则模型集中必须包含匀速运动模型。考虑到临近空间高超声速飞行器的运动特性,传统的Jerk模型受机动频率的影响较大,在跟踪此类目标时,不能体现自身优势;Singer模型具有比匀速(Constant Velocity,CV)模型和匀加速(Constant Acceleration,CA)模型更宽的覆盖范围,具有较大的机动适应性,但是当目标出现转弯机动时,跟踪效果较差;“当前”统计(Current Statistical,CS)模型能较为真实地反映目标机动范围和强度的变化,是目前较好的实用模型;转弯(Coordinate Turn,CT)模型针对转弯机动有较好的跟踪效果,这里采用的是一种修正的转弯模型(Modified Coordinate Turn,MCT),其基本思想为:当临近空间高超声速飞行器在高超声速巡航时,其相邻时刻的转弯角速度不可能发生突变,假定目标转弯角速度ω(t)服从一阶时间相关过程,结合目标转弯运动的几何关系得到MCT模型的连续时间系统状态方程,经拉普拉斯逆变换得到转弯模型离散系统状态转移矩阵,然后借助“当前”统计模型的思想,及时修正目标的“当前”角速度,较为准确地测量目标机动角速度的变化情况,使模型更复合目标的实际运动情况。由于篇幅的原因,这里不再赘述。
选择1个CV模型、5个CS模型和4个MCT模型,其最大加速度和最大角速度能够覆盖临近空间高超声速飞行器的可能机动情况。
假设1 模型的选择符合独立性与完备性的条件:
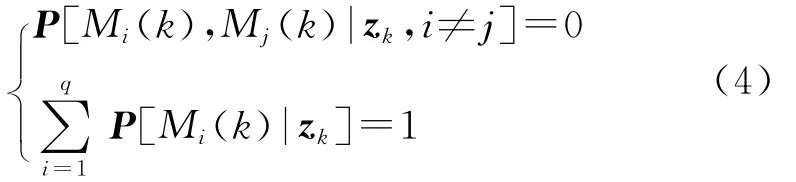
式中:Mi(k)为k时刻的模型Mi,zk为k时刻的观测值,q为模型总数。
2.2 建立模型有向图
模型之间的连通关系是根据目标类型和目标可能的机动情况等先验知识来确定。例如,载有攻击性武器的临近空间高超声速飞行器和单纯进行电子侦察的临近空间高超声速飞行器,其可能机动形式是不同的,而不管何种类型的目标,在一个采样周期内,目标不能从加速度最小的状态跳转到加速度最大的状态,故最大加速度amax和最小加速度amin不毗邻,最大角速度ωmax和最小角速度ωmin也不毗邻,当目标的加速度或者角速度较小时,其可能的机动形式相对较多,其他的与此类似。建立各模型之间的连通关系,如图1所示。
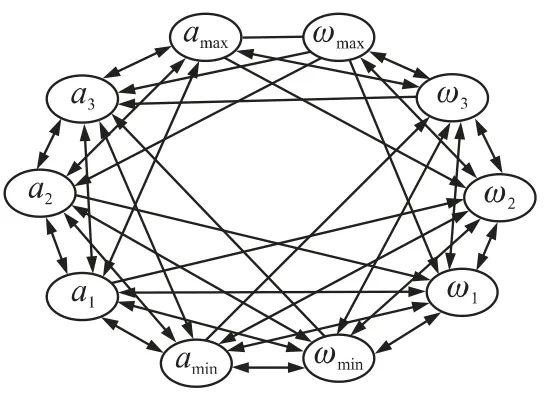
图1 模型有向图
显然,如果在一个总模型数为q,每个模型子集中的模型个数为b的系统中,模型子集的个数qmk最多为
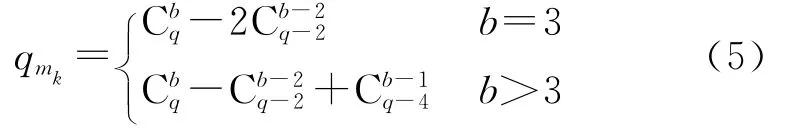
采用有向图的方法,其模型组合数远远超过传统方法。
假设2 模型间的转移服从状态有限、时间离散的时齐马尔科夫链,其马尔科夫转移概率为
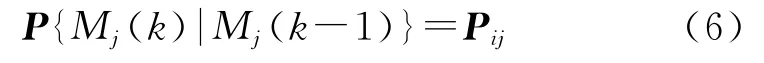
式中:Mj(k)为k时刻的模型Mj,Pij是根据先验知识来确定的,2个毗邻的模型其转移概率较大,而不直接连通的模型其转移概率为0。假设目标所有可能机动形式的一个强覆盖包含q个模型,每个模型子集包含b个模型(这里取b=4)。若k-1时刻系统模型子集为{a3a2ωminω1},交互输出时计算各子模型的后验概率,假设Ma2(k-1)的最大,如果后验概率为Pωmin(k-1)<Pω2(k-1)<Pa3(k-1)<Pa2(k-1),则在下一时刻要保留模型Ma2(k-1)和Ma3(k-1),将这2个模型的滤波值作为系统的输出和下一时刻的初始化值,根据系统所有模型之间的转移概率Pij,选择从模型Ma2(k-1)转移到其它模型概率最大的前2个模型(不与上一时刻参与计算的 模 型 重 复),假 设 为Mamax(k-1)和Mωmax(k-1),用 来 取 代 模 型Mω1(k-1)和Mωmin(k-1),则 在k时 刻 运 行 模 型 集 合{a2a3amaxωmax},同时进入下一个循环。
2.3 滤波计算
滤波计算指在模型集自适应选定参与计算的模型后,各模型进行跟踪滤波,对于非线性系统采用扩展卡尔曼滤波方法(Extended Kalman Filtering,EKF),计算方法与传统IMM 算法相同,具体方法见文献[10]。
3 仿真
3.1 仿真场景
假设飞行器的初始状态:x方向的距离为10km,速度为1 000m/s,加速度为0;y方向的距离为10km,速度为900m/s,加速度为0。总飞行时间为170s。飞行器发生机动时刻及对应的机动形式如表1所示,表中tj为机动时刻。传感器能够连续探测到目标在X-Y平面的位置和速度(含有噪声),量测周期T=1s。

表1 目标机动运动情况表
模型集合中包含10个子模型:1个CV模型,5个“当前”统计模型的最大加速度分别为-120m/s2,-90m/s2,60m/s2,90m/s2,120m/s2;4个转弯模型的最大角速度分别为-0.3rad/s,-0.2rad/s,0.2rad/s,0.3rad/s。所有模型之间的转移概率矩阵Pij根据目标的可能机动情况来确定,每一时刻参与计算的模型之间的概率转移矩阵与IMM算法的相同。为了便于说明,选择传统的LMS-VSMM算法作为对比,其模型集合为:1个CV模型、2个CS模型和1个MCT模型,模型参数与DG-VSMM算法的相同。在Matlab7.1中进行100次Monte-Carlo仿真。
3.2 结果分析
为了说明全过程的跟踪效果,针对每一个观测点,定义位置和速度均方根误差为
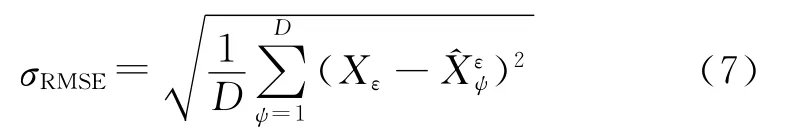
式中:Xε为状态向量的第ε个量测值,为第ψ次仿真的第ε个估计值,D为 Monte-Carlo仿真次数。
当状态噪声和量测噪声均方根分别为r1=100,r2=100时,得到2种跟踪算法的滤波轨迹如图2所示。

图2 滤波轨迹与真实值比较(r1=r2=100)
位置和速度均方根误差分别如图3、图4所示。
从图3和图4中可以看出,当目标运动状态相对较稳定时,如匀速或者加速巡航时,2种算法的跟踪效果相当;当目标加速度发生突变或者机动形式变化时,新算法跟踪结果较稳定,而LMS-VSMM算法会出现误差变大,特别是速度均方根误差体现得更明显,从总体来看,新算法的位置和速度均方根误差要小于LMS-VSMM算法的。

图3 位置均方根误差比较(r1=r2=100)

图4 速度均方根误差比较(r1=r2=100)
当状态噪声和量测噪声误差分别为r1=400,r2=400时,新算法和LMS-VSMM 算法的滤波轨迹如图5所示。
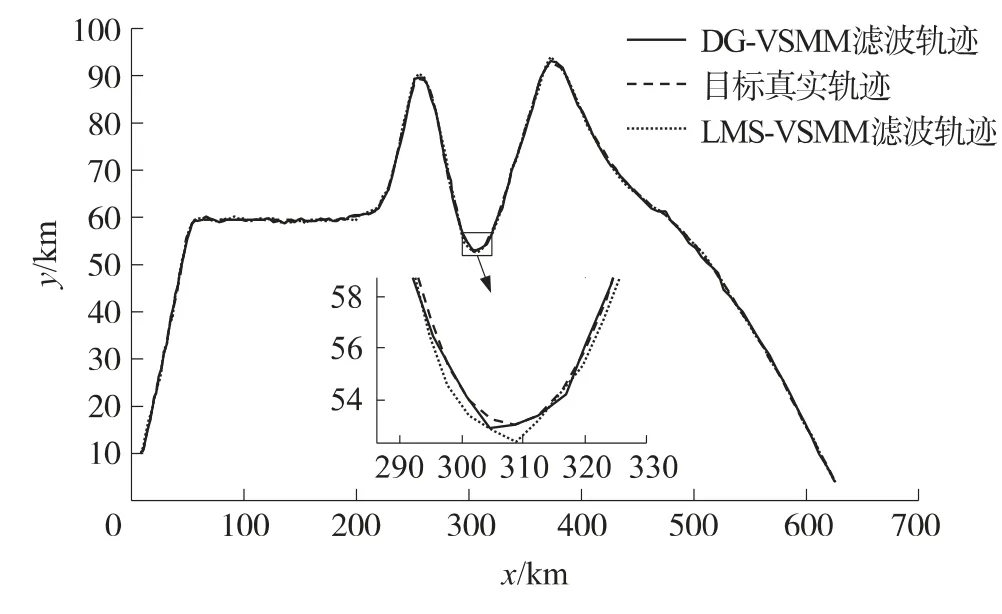
图5 滤波轨迹与真实值比较(r1=r2=400)
位置和速度均方根误差分别如图6、图7所示。
从图6和图7中可以看出,当系统状态噪声和量测噪声增大时,新算法和LMS-VSMM算法的位置均方根误差都增大,但是新算法增幅较小,而且当目标出现较强机动时,如目标的加速度发生突变,特别是目标的机动形式发生变化时,新算法的滤波结果更稳定,精度更高,而LMS-VSMM 算法出现误差急剧增大的现象。若新算法在多个模式切换之间不收敛,由于新算法能够保留最优模型,并根据后验概率选择最优模型的毗邻模型组成模型集,以最快速度实现收敛。从实用性角度来讲,新算法具有比传统算法更快的收敛率,这一点从图中目标发生连续转弯机动时的仿真结果可以看出。

图6 位置均方根误差比较(r1=r2=400)

图7 速度均方根误差比较(r1=r2=400)
从算法计算量方面分析,设模型集中模型总数为φ,每个周期参与计算的模型数为φ,记2个数进行比较的计算量为J1,则新算法完成对子模型滤波结果进行比较的计算量约为,选择模型集的计算量记为J2,LMS-VSMM算法中每个模型的概率和设定值进行比较的计算量为φJ1,综合判断的计算量为2J1,如果目标机动复杂,传统算法可能需要次计算才能达到最优,故新算法每个量测周期模型集跳转的计算量为,比 LMS-VSMM 算法[(φ+2)J1+J2]的小。
4 结论
本文分析了临近空间高超声速飞行器的目标特性,针对传统跟踪算法不能实现对此类目标进行有效跟踪的问题,提出了一种基于有向图的变结构多模型跟踪算法。通过选择模型集合、建立模型间的连通关系、设计自适应策略和交互计算,使每一时刻参与计算的模型都接近最优。该算法能够比传统VSMM算法更快地在模型子集之间跳转,更快地实现对目标的稳定跟踪,可适用于临近空间高超声速飞行器以及目标的运动模式空间很大、目标的运动状态高度时变(强机动)的情况。针对以临近空间高超声速飞行器为代表的“高、快、小”目标,设计更为恰当的跟踪算法,使算法的适应能力和针对性更强一些,是一个具有重要现实意义的课题,也是下一步的研究重点。
[1]马英,何麟书.实现高超声速跳跃式弹道关键问题的研究[J].弹道学报,2009,21(3):35-38.MA Ying,HE Lin-shu.Study on key problems of realizing hypersonic skip trajectory[J].Journal of Ballistics,2009,21(3):35-38.(in Chinese)
[2]HU R F,WU Z N,WU Z,et al.Aerodynamic map for soft and hard hypersonic level flight in near space[J].Acta Mech Sin,2009,25:571-575.
[3]关欣,赵静,何友.临近空间高超声速飞行器跟踪技术[J].四川兵工学报,2011,32(8):4-6.GUAN Xin,ZHAO Jing,HE You.Track technology of hypersonic aircraft in near space[J].Journal of Sichuan Ordnance,2011,32(8):4-6.(in Chinese)
[4]HOU L Q,LI H N,HUANG F M,et al.Tracking micro reentering USV with TDRS and ground stations using adaptive IMM method[C]//Proceeding of the IEEE International Conference on Information and Automation.Shenzhen:IEEE,2011:1-7.
[5]FOO P H,NG G W.Combining the interacting multiple model method with particle filters for maneuvering target tracking [J].IET Radar Sonar and Navigation,2011,5(3):234-255.
[6]QU H Q,PANG L P,LI S H.A novel interacting multiple model algorithm[J].Signal Processing,2009,89(11):2 171-2 177.
[7]LI X R,JILKOV V P.A survey of maneuvering target tracking partⅤ:multiple-model methods[J].IEEE Transactions on Aerospace and Electronic Systems,2005,41(4):1 255-1 321.
[8]LI X R,ZHANG Y M.Multiple-model estimation with variable structure partⅤ:likely-model set algorithm[J].IEEE trans on Aerospace and Electronic Systems,2001,36(2):448-466.
[9]LI X R,ZHANG X.Multiple-model estimation with variable structure partⅢ:model-group switching algorithm[J].IEEE Trans on Aerospace and Electronic Systems,1999,35(1):225-240.
[10]PENG D L,GU Y.IMM Algorithm for a 3Dhigh maneuvering target tracking[J].Lecture Notes in Computer Science,2011,6 729(1):529-536.
