变形牛顿环装置干涉结果的仿真模拟

郭中华，郑隆举

（兰州城市学院培黎工程技术学院，甘肃 兰州 730070）

牛顿环干涉实验的装置结构简单、便于操作、物理图像清晰，在物理教学中对等厚干涉原理的理解方面具有优势，是传统的普通光学实验项目之一，利用牛顿环干涉技术可以进行光学测量、光学检测等的应用［1－3］。

现在有很多对于扩展的变形牛顿环装置的理论和实验研究，这些变形装置除了能完成普通牛顿环干涉装置所能做的光学测量之外，还有其自身的特点和新的应用前景，下面就对典型几种变形牛顿环干涉装置进行分析。

1 牛顿环干涉基本装置及干涉结果仿真

牛顿环基本干涉装置的结构图如图1所示，由一块平凸透镜和平板玻璃构成。在平凸透镜和平板玻璃接触点建立坐标系，C为透镜的曲率圆心，R为透镜的曲率半径，rj为某一级干涉条纹半径，d为该处介质薄层厚度。从图1中的几何关系可知r2j＝R2－（R－d）2，由于介质薄层厚度d很小，略去高阶小量，从而有

垂直照射牛顿环，在反射光方向（即沿着 轴正向）观察干涉结果，由于双光束干涉光强近似相等，从而相干光的干涉光强为

干涉条纹的结果是由光在两透镜间介质薄层上、下表面的光程差决定的，再考虑光在上、下表面反射时的相位突变，则两束相干光的相位差为连同（1）式结果代入（2）式可得透镜上任一点处的干涉光强为

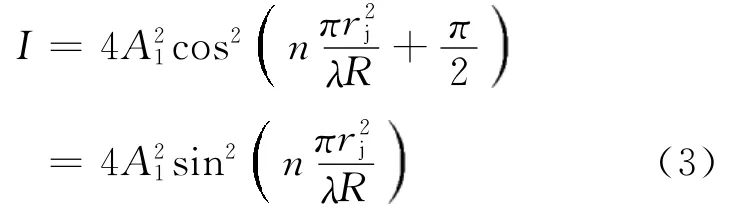
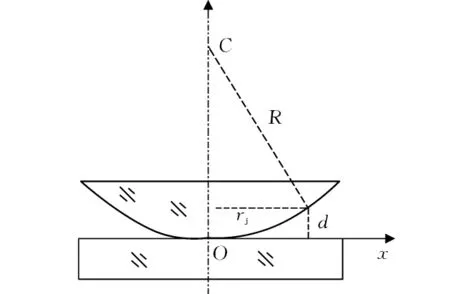
图1 牛顿环干涉结构图

模拟中采用入射光λ＝632.8 n m，透镜R＝2 m，介质折射率n＝1，在xoy平面取［－4 mm，4 mm］的区域，任一级干涉条纹半径可由r2＝x2＋y2代入，计算每点光强，绘制光强的灰度图像及强度曲线如图2所示。

图2 牛顿环干涉条纹及相对光强分布曲线

牛顿环干涉的仿真模拟是研究等厚干涉问题的有效途径和方法，具有一定的应用价值，仿真中可以控制各种参数的变化［4］对干涉结果进行分析，也可以设定参数利用循环结构或GUI做成动画来直观的了解干涉条纹的变化［5］，因为实际应用中往往是通过干涉条纹的变化去进行一些光学测量。

2 变形牛顿环干涉装置及干涉结果仿真

能产生牛顿环干涉的变形装置有很多，实际上任两块透镜满足了一定的条件，在曲率圆心为轴的傍轴区域，单色光垂直照射下都可以观察到干涉结果［6］，文献［5］中列举了各种类型镜片构成的牛顿环装置，下面就典型的几种来做说明。

2.1 接触式变形装置

2.1.1 平凸透镜和平凸透镜组成的实验装置

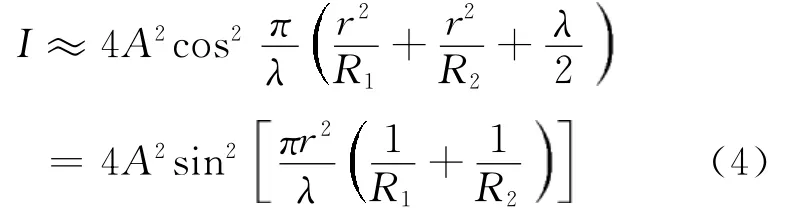
图3 平凸 －平凸透镜组合装置

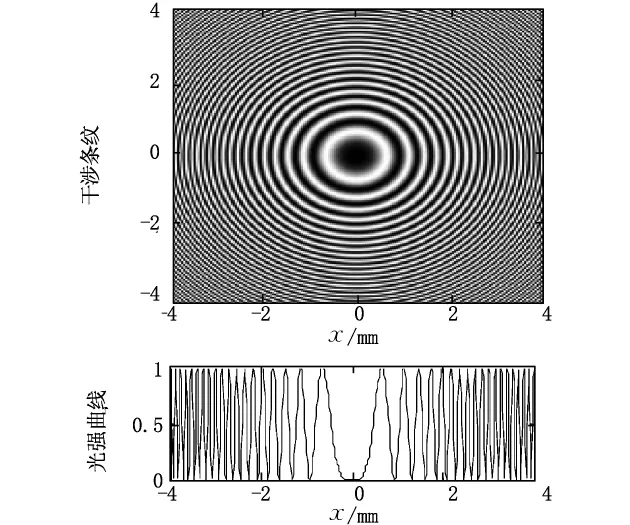
图4 干涉条纹及相对光强分布曲线

可以比较出图4和图2条纹在相同规格下干涉结果的一些区别，实际上透镜曲率半径越大，或是形成的气模越薄，实验效果或是所做测量的精度越好［7］。

2.1.2 平凸透镜和平凹透镜组成的实验装置

装置结构如图5所示，不妨设R1＜R2，这样的装置结构可以测定凹曲面的曲率半径，也可利用来进行光学球面加工质量的检测。

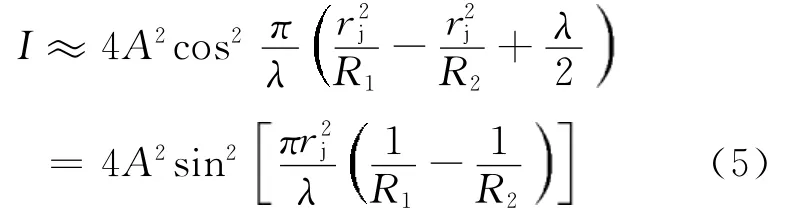
图5 平凸 －平凹透镜组合装置

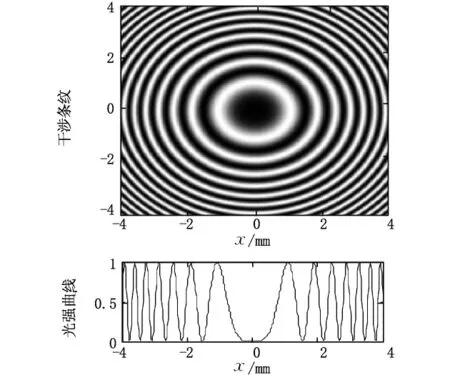
图6 干涉条纹及相对光强分布曲线

2.1.3 平凹透镜和平板玻璃组成的实验装置

平凸透镜组成的装置在实验测量过程中，由于固定螺丝的松紧程度不好调节，容易使平凸透镜处于不稳定状态，且会导致透镜的形变，从而产生系统误差。装置中的平凸透镜可由一平凹透镜来替代，结构如图7所示，这种装置为外圈接触，受压形变不大，所得干涉图样清晰，测量结果较好，早在一些院校的实验中使用［8］。

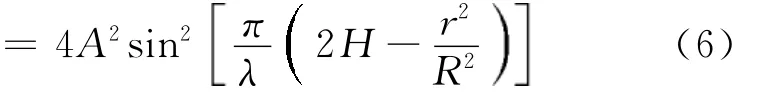
设此平凹透镜规格和图1中一样，其余参数不变，则模拟干涉图样和光强曲线如图8所示。

图7 平凹透镜 －平板玻璃组合装置

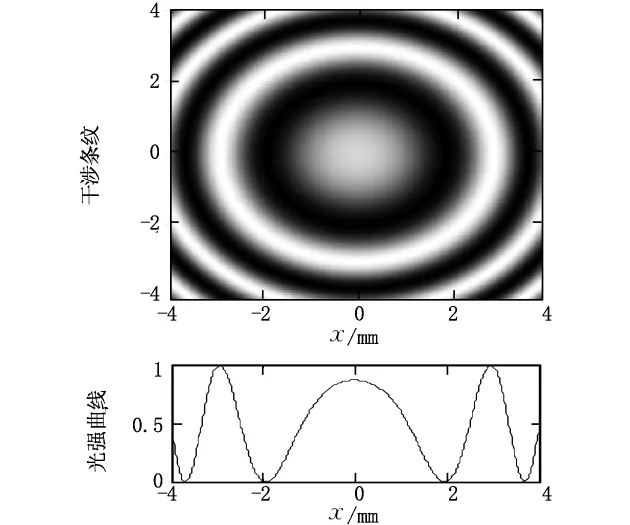
图8 干涉条纹及相对光强分布曲线

2.2 非接触式变形装置

非接触式牛顿环干涉结构可分为几种：平凸－平板非接触式干涉结构（其结果与图2类似，故略）、平凸 －平凸非接触式干涉结构（如图9所示）和平凸 –平凹非接触式干涉结构（如图11所示）。非接触式干涉结构避免了接触式干涉装置由于接触点应力而导致的球冠畸变，同样可用于光学检测，利用光电转换装置及CCD检数技术，它还可应用于微位移光学传感技术，其灵敏度相近于F－P位移传感装置。

与上述分析类似，平凸－平凸非接触式干涉结构介质薄层中两相干光的光程差为δ＝2d＋＝2（d1＋d2＋h）＋，其中h为中央介质薄层的厚度，则由（2）式推导出干涉环纹的光强分布为

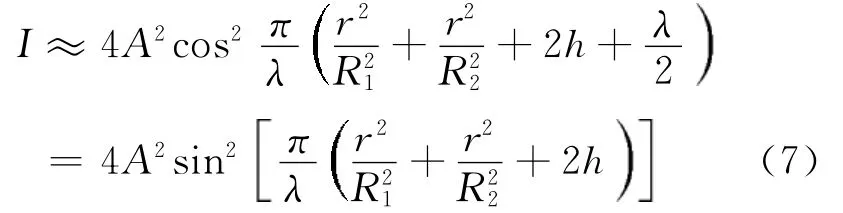
其余参数不变，则模拟干涉图样和光强曲线如图10所示。

与上述分析类似，平凸 －平凹非接触式干涉结构介质薄层中两相干光的光程差为δ＝2d＋＝2（d＋h－d）＋，则由（2）式推导出干涉环12纹的光强分布为

其余参数不变，则模拟干涉图样和光强曲线如图12所示。

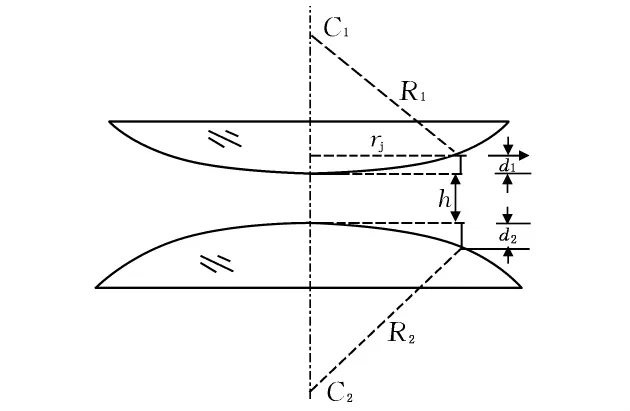
图9 平凸 －平凸透镜组合装置

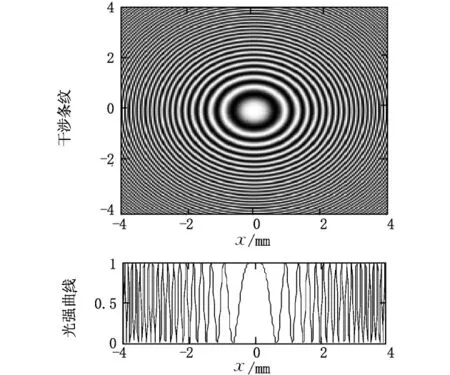
图10 干涉条纹及相对光强分布曲线

2.3 浅近切割牛顿环干涉装置

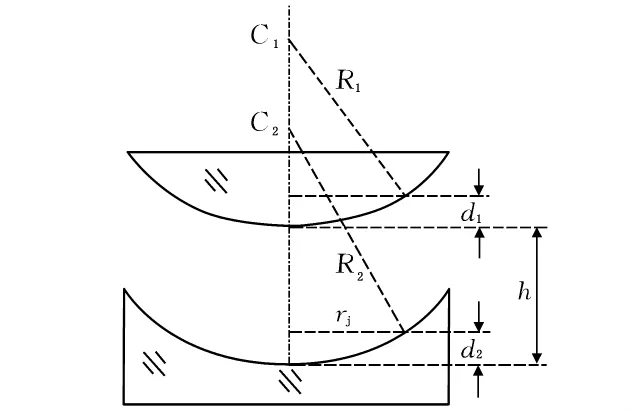
图11 平凸 －平凸透镜组合装置

图12 干涉条纹及相对光强分布曲线

将正常牛顿环装置的平凸透镜球冠顶点处截去高度h（h≪R）的小球冠，则原透镜变成一球缺（上下底面为圆形平面且平行），再使这一球缺顶部与平板玻璃密切啮合（是否有空气隙不影响干涉条纹结果，只是中央圆斑的亮暗情况不同），就形成截顶式浅近切割牛顿环装置，如图13所示。

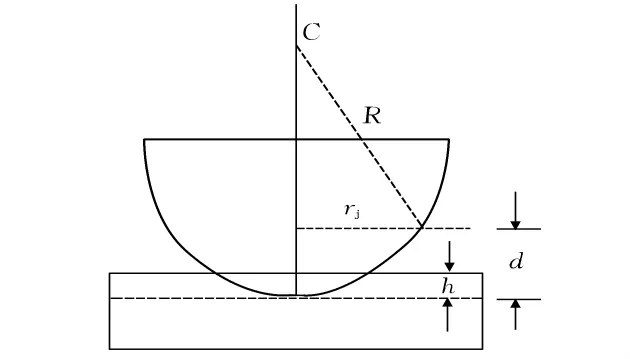
图13 截顶式浅近切割牛顿环结构示意

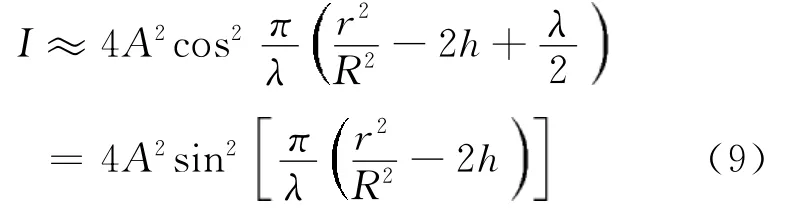
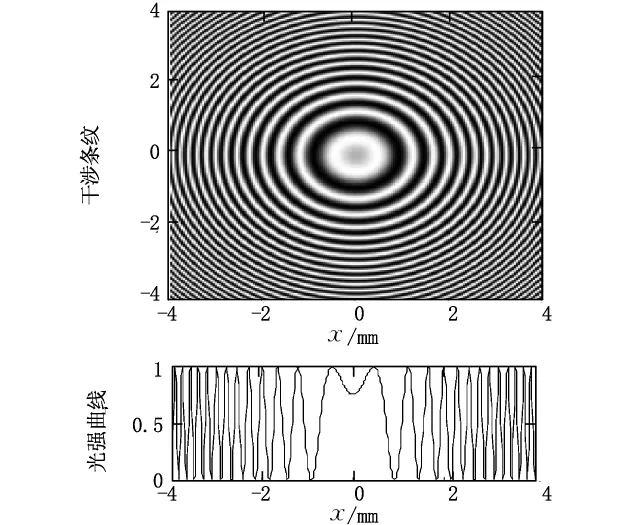
图14 干涉条纹及相对光强分布曲线

此外，将球冠顶部嵌入一平板玻璃表面一定深度h（h≪R），就构成了嵌入式浅近切割牛顿环干涉结构。但实际中将球冠顶部嵌入一平板玻璃表面一定深度这种情况比较难实现，最易做到的是嵌入液态介质中，由于液体表面张力和湿润角度的关系，使得液面与玻璃表面接触处的圆环以外不是严格水平面，这种情况下可以利用变形的牛顿环分布情况来研究液体在球形玻璃表面的湿润规律及液面的形状［9］。另外利用这种变形分布，还可研究一种金属分子在另一种金属薄膜表面的沉积分布规律［10］。

还有其它一些浅近切割牛顿环装置，也可类似去模拟，但实际应用中，由于制作工艺复杂，涉及到的应用很少，故略去不论。

3 结 论

文章详细分析了各种变形牛顿环干涉装置，并借助MATLAB的数据可视化功能对各种装置的干涉结果进行了仿真模拟，在设定参数基本相同的情况下，从模拟结果可以比较出各种变形干涉装置条纹的基本特点，从而对各种相应的实际应用有大致的了解。这种计算机仿真方法扩展了研究问题的途径，使教学直观化，并具有一定的实用价值。

［1］姚启钧.光学教程［M］.4版.北京：高等教育出版社，2008：33－56.

［2］谭毅.牛顿环实验的仿真研究［J］.信息技术，2011（5）：27－29.

［3］王必利.利用牛顿环实验测定玻璃的弹性模量［J］.大学物理实验，2011，25（2）：44－46.

［4］李明新，等.关于牛顿环实验数学的几点探讨［J］.大学物理实验，1996，43（2）：57－59.

［5］钞曦旭.MATLABN及其在大学物理课程中的应用［M］.西安：陕西师范大学出版社，2006：277－279.

［6］周希尚，杨之昌.牛顿环实验综述［J］.物理实验，1993，13（2）：66－69.

［7］张和民，等.牛顿环装置镜片结构的探讨［J］.西南师范大学学报：自然科学版，1994，19（3）：328－332.

［8］贾玉润，等.大学物理实验［M］.上海：复旦大学出版社，1987：310－313.

［9］周国全，郭长明.再论牛顿环干涉装置的若干变异结构［J］.武汉大学学报：理学版，2005，51（1）：51－54.

［10］Edwards H W.Newton’s Rings in Transparent Metallic Fil ms［J］.Phys Rev，1931，38（166）：373－374.