基于EMD分解的测量误差分离方法研究
2013-12-24
基于EMD分解的测量误差分离方法研究
汪伟1,陈海龙1,刘裕鹏2
(1.军械工程学院,河北石家庄050003;2.沈阳军代局驻127厂军代室,黑龙江齐齐哈尔161000)
摘要:振动测试可以通过位移信号一次求导、二次求导得到振动信号的速度、加速度。针对位移信号求导过程存在使原始信号中误差放大的问题,该文将EMD经验模态分解方法应用到振动测试中,有效地从位移信号中分离出系统误差和随机误差,减小求导后速度、加速度信号中的误差信号,并通过仿真和实验验证该方法的有效性。
关键词:经验模态分解;振动测试;测量误差;误差分离
收到修改稿日期:2012-12-04
0 引 言
振动测试在新产品设计、修订相应环境标准、可靠性试验、环境试验以及机械故障诊断等方面有着广泛应用。位移传感器测量位移是属于绝对式测量,不存在误差累计问题。但在采样频率很高时,求导后得到的速度、加速度信号中有很大的误差信号。对测量数据的误差进行修正,提高测试精度的关键技术在于如何分离测量数据中的系统误差和随机误差。现在测量误差的分离方法使用较为广泛的有最小二乘回归法、均值滤波法、傅里叶级数逼近法、小波和小波包分解法等。这些方法存在模型阶数、基函数不易选取,或者误差分离精度难以提高等问题[1-2]。本文提出的基于经验模态分解(EMD)误差分离方法是自适应分解,不需要选择确定模型阶数、基函数,而且具有较高的信噪比[3]。
1 经验模态分解
经验模态分解(empirical mode decomposition,简称EMD)方法是由美国NASA的黄锷博士提出的一种信号处理方法。它依据数据自身的时间尺度特征进行信号分解,无须预先设定任何基函数。这一点与建立在先验性的谐波基函数和小波基函数上的傅里叶分解与小波分解方法具有本质差别。由于这样的特点,EMD方法理论上可以用于任何类型的信号分解[4-5]。
由经验模态分解出来的固有模态函数满足约束条件:
(1)整个数据序列中,极值点的数量与过零点的数量相等或至多相差为1。
(2)信号上任意一点,由局部极大值点确定的包络线和由局部极小值点确定的包络线的均值均为0,即信号关于时间轴局部对称。
利用两个连续的处理结果之间的标准差SD来判断第二个条件是否满足,SD值取0.2~0.3时为宜,既可保证IMF的线性和稳定性,又可使IMF具有相应的物理意义。
(1)数据初始化,令r(0t)=x(t),i=1;
(2)提取第i个经验模态分量:
1)使h0=r(it),k=1;
2)对hk-(1t)取其局部的极大值和极小值;
3)对hk-(1t)极大值点和极小值点分别通过插值函数连接起来,形成上下包络;
4)计算上下包络的平均值mk-(1t);
5)计算h(it)=hk-(1t)-mk-(1t);
6)如果满足停止条件,则h(t)=c(it),否则转到2),并且使k=k+1;
(3)计算r(it)=ri-(1t)-c(it),如果在r(it)中存在的极值点数多于2个,则转到2)并且使i=i+1,否则停止分解,r(it)代表原始数据的残余量。最后得到的
n分解结果为x(t)=Σc(it)+rn这样就获得了n个经
1验模态分量c(it)和一个残余量rn。n个经验模态分量代表了原始光谱曲线中包含的不同时间尺度的特征信号,通常EMD分解出来的前几个IMF分量集中了原信号中最显著、最重要的信息,残余量rn代表了原始信号曲线中的趋势量信息[6]。
2 振动测试误差分离方法
位移传感器,又称线性传感器,是利用各种元件检测对象的物理变化量,通过将该变化量换算为距离。现代工艺的位移传感器具有频带宽、灵敏度高、时间常数小等特点。一阶线性系统的阶跃响应函数为

式中:KA——稳态值;
τ——时间常数。
得到位移传感器过度响应误差为

在时间常数τ很小的情况下,由系统过度响应造成的动态误差值非常小。根据位移传感器测量误差的特点,说明线性系统静态误差和动态误差虽然存有差异,但其变化规律是相似的。因此可以通过静态测量数据进行EMD分解,得到的IMF分量和趋势项来确定动态测量误差的形式来提取系统误差。先对测量系统先进行位移不变的静态测试,将测得数据进行EMD模态分解,得到一组IMF分量和残余量。再进行位移变化的动态测试,对测得数据进行EMD分解,同样得到一组IMF分量和残余量。分别对两组信号IMF分量进行傅里叶变换,动态测试IMF分量中幅值、频率与静态测试IMF分量相同的分量之和应为理论上系统误差的频率成分。在原始信号中减去两组数据中形同频率成分的IMF分量后得到有用信号。
3 系统误差的分离与仿真
按照系统误差变化特征特点,设计包含有线性变化系统误差、周期性变化系统误差以及指数变化系统3种形式系统误差组成的系统误差进行仿真实验,说明EMD分解提取系统误差的有效性。
仿真实验中假设系统误差s(t)的表达式为

测量信号x(t)由两个部分组成,一部分是系统误差s(t),另一部分是有效信号d(t)。

3.1静态测量
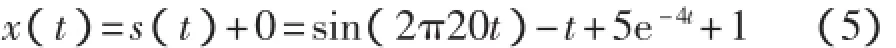
不考虑随机误差有效信号为零时测量数据为对x(t)进行EMD分解相当于对系统误差进行模态分解,其结果如图1所示。

图1 系统误差EMD分解结果
3.2测量简单正弦振动信号
假设有效信号是频率为5 Hz的正弦信号:

则测量信号为

对x(t)进行EMD分解,其结果如图2所示。
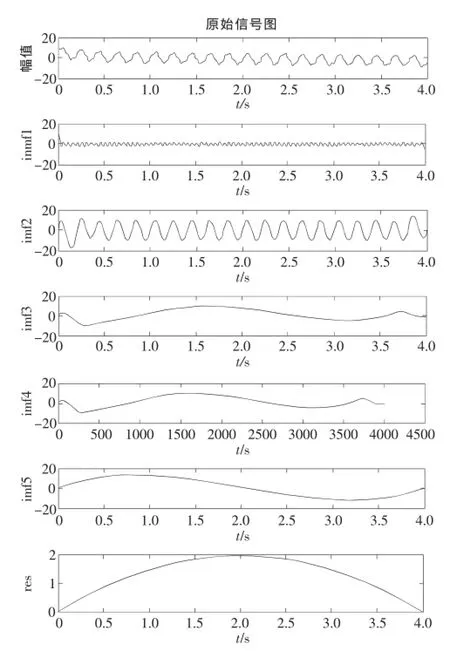
图2 测量信号EMD分解结果
对图2中频率与图1中具有相同频率的分量imf1、imf3、imf4、imf5和res相加得到系统误差。
图3(a)中给出了分离误差和系统误差。可以假设利用EMD分解方法可有效的从简单正弦振动信号中分离出复杂的系统误差。
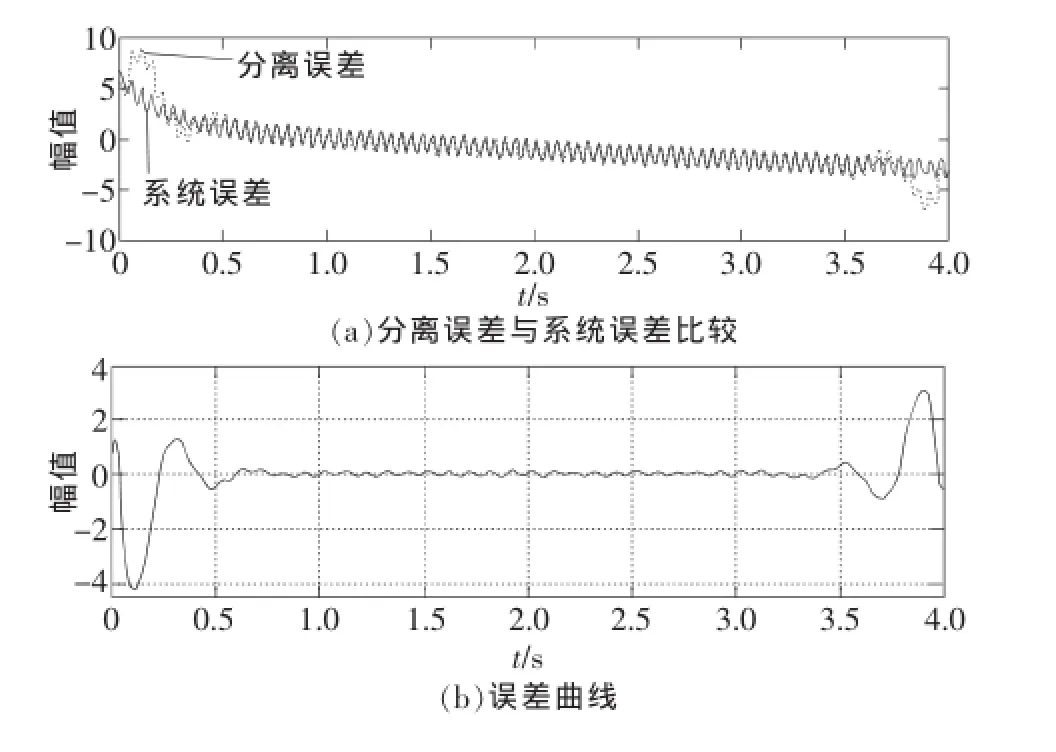
图3 误差分离结果
3.3多个正弦信号叠加测试仿真
由于振动信号大多为多个频率的正弦振动信号的叠加,假设两个正弦叠加的有用信号d(t)为

则测量得到的信号x(t)为

对x(t)信号进行EMD分解结果如图4所示。?

图4 测量信号EMD分解结果
由图5(a)可以看出多个正弦振动信号分离出的系统误差和实际系统误差相似度同样很高,再由图5(b)给出的误差曲线看出分离出系统误差后的误差总体非常小。但由图3(b)和图5(b)可以看出由于EMD算法的端点飞翼现象使得数据两端误差较大。在处理过程中,对较长数据处理时可以通过不断抛弃两端的数据来保证所得包络失真度最小。对于一个较短数据序列来说,一般通过使用一些改进的样条函数方法或者在实测信号两端进行延拓,使得边界效应移到延拓后的两端,从而减小边界信号对实测信号的影响[7]。
4 实验验证
本文实验是采用拉绳位移传感器实时测量火炮后座运动,通过对比分离后得到实际位移曲线与理论位移曲线对比来说明EMD分解方法分离系统误差的有效性。
4.1系统误差分析
拉绳传感器静态测量数据如图6所示。

图6 静态测试数据
从图6看出静态测试数据成规律的变化,对静态数据进行EMD分解结果如图7所示。
图7中得到的各个imf分量可以看成系统误差中各个频率的分量。
4.2系统误差分离
拉绳传感器测量位移数据如图8所示。对动态测量数据进行EMD分解,结果见图9。对静态和动态各模态分量做傅里叶变换,得到频谱图如图10所示。
将动态数据中与静态数据中相似频率和幅值的imf2、imf3、imf4分量相叠加得到分离误差数据曲线如图11所示。
对比图6静态测量数据和图11分离出来的误差可以看出,利用和静态误差相同频率的imf分量叠加出来的曲线和静态测量数据曲线具有很高的相似
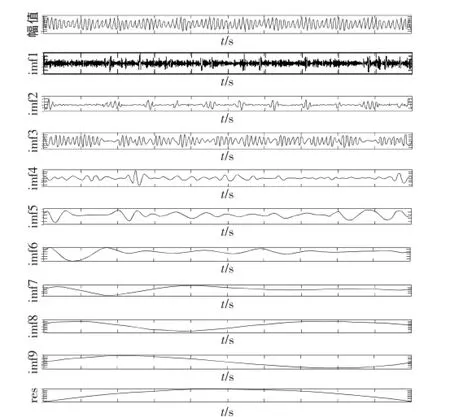
图7 静态测试数据EMD分解结果

图8 动态位移曲线

图9 动态测试数据EMD分解结果

图10 静态、动态数据各模态分量频谱
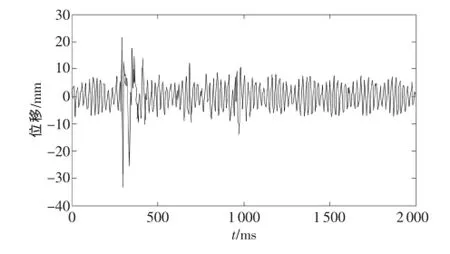
图11 分离误差曲线
性。减去动态测试数据分离出来的误差数据得到动态测量曲线如图12所示。
对比分离误差后的位移曲线和未分离误差的位移曲线如图13所示。可以看出两个曲线吻合度很高,分离误差后的曲线波动明显小于原始测量位移曲线。
5 结束语
本文通过仿真和实验证明,利用EMD经验模态分解的方法可以有效地从位移信号分离出系统误差。但EMD分解过程中会出现一些虚假模态分量,这些虚假模态分量给判断信号中的误差频率成分造成一定困难。对于消除虚假模态分量方法已有相关研究[8],但对于虚假模态分量与真实模态分量混叠于同阶本征模态分量的情况,还存在困难。对于如何分离出有效信号模态分量中的虚假模态分量,提高EMD分离误差精度还需进一步进行研究。

图12 分离误差后动态位移曲线
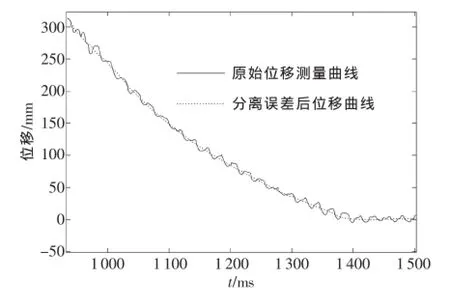
图13 原始信号和分离误差后信号比较
参考文献
[1] 李世平,付宇,张进.一种基于EMD的系统误差分离方法[J] .中国测试,2011,37(3):9-13,36.
[2] 张俊玲.减小测量误差的测量方法研究[J] .大学物理实验,2010,23(1):71-73.
[3] 史恒,李桂林,王伟.基于总体经验模式分解的地震信号随机噪声消除[J] .地球物理学进展,2011,26(1):71-78.
[4] 胥保春,袁慎芳. IMF筛选条件分析及新的停止条件[J] .振动、测试与诊断,2011,31(3):348-353.
[5] 甘露,周龙,尤新革. HHT方法在探地雷达回波信号特征提取上的应用[J] .电子设计工程,2012,20(12):61-63.
[6] 赵振昊,沈毅,王冬明.导引头的EMD-EF组合滤波方法[J] .系统工程与电子技术,2011,33(8):1861-1864.
[7] 杜陈艳,张榆峰,杨平,等.经验模态分解边缘效应抑制方法综述[J] .仪器仪表学报,2009,30(1):55-60.
[8] 黄迪山.经验模态分解中虚假模态分量消除法[J] .振动、测试与诊断,2011,31(3):381-384.
Measurement error separation method based on EMD
WANG Wei1,CHEN Hai-long1,LIU Yu-peng2
(1. Ordnance Engineering College,Shijiazhuang 050003,China;2. Shenyang Military Representative Office in 127 Factory,Qiqihar 161000,China)
Abstract:Vibration speed and acceleration can be obtained from the first and second derivatives of displacement signal respectively. However,there is a problem of error enlargement in the derivation of displacement signal. This paper applied EMD decomposition method to vibration test,which can separate system and random errors from the displacement signal effectively. Simulation results and experimental results verified the effectiveness of this method.
Key words:EMD;vibration test;measurement error;error separation
收稿日期:2012-10-24;
doi:10.11857/j.issn.1674-5124.2013.05.003
文章编号:1674-5124(2013)05-0011-05
文献标志码:A
中图分类号:O241.1;TM930.115;TB53;O241.1
作者简介:汪伟(1963-),男,陕西西安市人,副教授,博士,主要从事机械测试和故障诊断研究。
