超声相位差法测量杨氏模量

2013-12-23郭启凯郭敏强张亚萍闫向宏

实验技术与管理 2013年2期

郭启凯，郭敏强，李超，张亚萍，闫向宏

（中国石油大学（华东）物理与光电工程系，山东青岛 266580）

超声波测距是一种传统而实用的非接触测量方法，和激光、涡流、无线电测距方法相比，具有近距范围内不受光线影响、结构简单、成本低等特点，在恶劣环境中也具有一定的适用性，在工业自动控制、建筑工程测量和机器视觉识别等领域得到广泛应用［1－6］。超声测距的传统方法是脉冲回波法，主要是通过计算超声波发射探头发射出超声波至超声波接收探头接收到回波信号的时间来确定探头至被测物体的距离［7］。脉冲回波法的测量原理简单，但是精确度不高。近几年来，相位差法因其有较高的测量精度越来越受到重视，相位差法超声测距是利用发射波和被目标反射的接收回波之间声波的相位差包含的距离信息来实现对被测目标距离的测量［8］。

杨氏模量是表征固体材料形变与内应力关系、描述固体材料抵抗形变能力的重要物理量，因此，它是工程技术中机械构件选材时的重要参数之一［9］。测量杨氏模量的方法很多，传统测量中主要采用静态拉伸法。通常采用静态拉伸法测量金属丝微小的形变量时，应用光杠杆的放大原理［10］，光杠杆法的测量过程耗时较长、过程复杂。本文根据相位差法测距原理实现了对金属丝杨氏模量的测量，结果表明，该方法具有测量时间短、自动化程度高和操作方便等优点。

1 相位差法测量杨氏模量原理

1.1 相位差法测距原理

设在初始时刻发射信号为

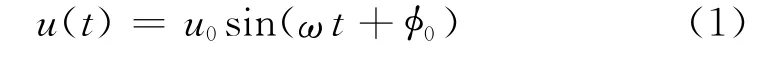
忽略信号经过电路时引起的相位差，则被接收换能器接收的信号为

则两目标的距离为

式中f 为超声波的频率。

1.2 相位差法测量杨氏模量原理

相位差法测量杨氏模量装置如图1 所示，在待测金属丝下方悬挂一小烧杯，将发射换能器固定于其下方。在发射换能器的正下方平行放置接收换能器，两换能器与测量仪器相连。测量时，首先在烧杯中加入质量为M1的铁砂，质量要适中，以保证金属丝被拉紧，启动测量装置，测出此时的相位差Δφ1；然后向烧杯中缓慢加入更多铁砂（测量发现，若一次加入铁砂过多会导致仪器的示值发生较大偏差），随着烧杯中铁砂质量的增加，发射换能器随金属丝一起下降，使得两换能器之间的距离缩短。设铁砂的质量为M2时停止加入铁砂，启动测量装置，测出此时的相位差Δφ2。

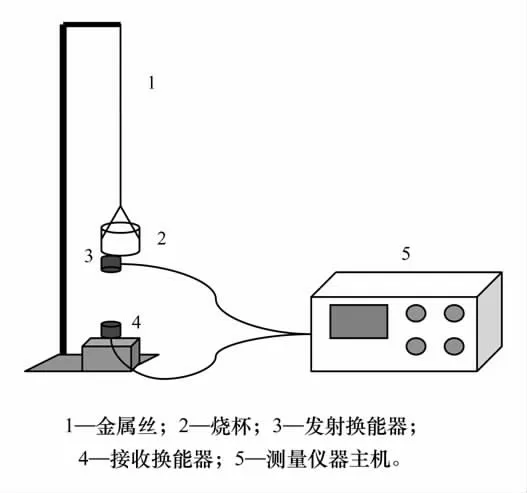
图1 超声相位差法测量杨氏模量系统装置图

利用公式（4）可以求得加入质量为M2－M1的铁砂时，金属丝的长度变化量ΔL 为

如果金属丝的直径为d、起始长度为L，则金属丝的杨氏模量E 可表示为

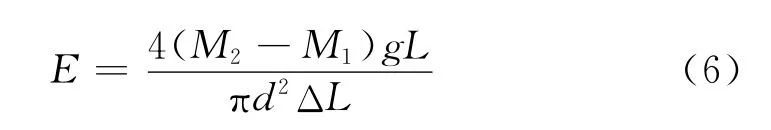
式中g 为重力加速度。

2 测量仪器硬件设计

测量仪器主机内部结构如图2所示，主要由信号发生器、超声测量、温度测量和信号处理4部分组成。其中信号发生器由AD9833可编程波形发生器、放大器和射极跟随器组成［11］，用于产生峰峰值稳定、频率可调的正弦信号。该正弦信号分为2路，一路经驱动芯片放大后激励发射换能器向空气介质中辐射声波，声波传播一定距离后被固定在底座上的接收换能器接收（接收换能器上同时固定有温度传感器），接收换能器将超声信号转换为电信号并经放大器放大后传送给信号处理部分；另一路信号直接传送给信号处理部分。由温度传感器实时测量周围的温度（温度对声速有影响），信号处理器根据测得温度值对声速值进行修正。信号处理器由电平抬升器、稳压电源和DSP 芯片组成，该部分的核心器件是DSP 芯片，它是专门为快速实现各种数字信号处理算法而设计的、具有特殊结构、进行高速实时处理的专用微处理器［12］。通过内置程序将接收到的温度值对声速进行修正反馈、计算，并将结果输出到控制面板的LCD 显示屏上，从而实现对相位差的精确测量。

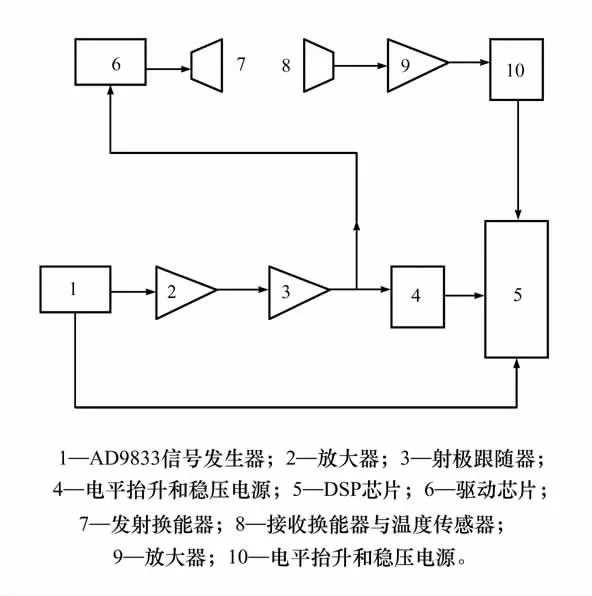
图2 测量仪器内部结构

3 实验结果与分析

测量前，首先对测量仪器的测量精度进行定标。实验时将发射换能器固定于螺旋测微器底端，并竖直放置在支架上；在发射换能器的正下方一定距离处，水平放置接收换能器，将两换能器与实验测量仪器相连。启动仪器，缓慢转动螺旋测微器，使得发射换能器缓慢下移，记录下移距离与仪器所显示相位差的对应关系，测量结果如表1所示。

表1 下移距离与仪器所显示相位差的对应关系

利用逐差法对表1中的数据进行处理，得到下移距离每变化0.5mm 时相位差改变值的算术平均值为18.2°。则每变化一个相位，换能器下移的距离为0.03mm。

可见，本测量仪器的测量精度为0.03mm。

实验时，选用长度L＝120cm，直径d＝0.501 mm 的金属丝。首先在烧杯中加入1kg的铁砂，使得金属丝完全绷紧，记录此时的相位差；然后缓慢向烧杯中加入铁砂，每隔1kg记录一次相位差和拉伸长度，所得数据表2中。利用式（8）给出的测量仪器的精度计算出相应的拉伸长度ΔL，也记录在表2中。

表2 超声相位差法测杨氏模量记录表

采用逐差法对数据进行处理，求得每增加1kg铁砂时，金属丝的拉伸长度为0.31 mm。由式（6）求得该金属丝的杨氏模量值为1.96×1011N／m2。与静态拉伸法测得的结果1.95×1011N／m2相比误差仅为0.5%，由此可见，运用超声相位差法测量杨氏模量的精确度与静态拉伸法相近。

4 结束语

本文根据相位差法测距原理设计的钢丝杨氏模量测量系统具有测量精度高、操作简单、测量时间短的优点，可以满足绝大多数场合的测量要求，因此，具有较好的应用前景。该测量系统不仅可以测量杨氏模量，还可以用于其他涉及微距测量的实验中，可以大大提高实验效率。如若基于此原理制作更加精确的测量仪器，则完全可以投入到商业化生产中。

（

）

［1］郭蓉，廖娜，郭丽.基于STC89C51单片机的超声波测距系统设计与实现［J］.石油仪器，2010，24（5）：13－17.

［2］路锦正，王建勤，杨绍国，等.超声波测距仪的设计［J］.传感器技术，2002，21（8）：29－34.

［3］沈常宇，郭宝金.相位比较法高精度超声测距研究［J］.传感技术学报，2010，23（6）：893－895.

［4］潘登，潘宗预.超声波测距精度的探讨［J］.中国包装工业，2003（113）：39－40.

［5］李玉滨，孙皓.基于C8051F020单片机的超声测距仪设计［J］.山东交通学院学报，2008，16（1）：69－72.

［6］赵珂.时差法超声测距仪的研制［J］.国外电子元器件，2005（1）：65－67.

［7］杨庆，陈桂明，董振旗.一种改进的高精度超声测距方法研究［J］.计算机技术与发展，2010，20（12）：209－212.

［8］Grmmel P M.Improve ultrasonic detection using the analytic signal magnitude［J］.Elsevier，1981，19（2）：73－76.

［9］李书光，王殿生.物理实验教程［M］.东营：中国石油大学出版社，2006：68.

［10］王玉清.固体杨氏模量的测量［J］.大学物理实验，2007，20（3）：20－22.