非线型固体杨氏模量测量

2013-12-23刘竹琴刘艳峰

实验技术与管理 2013年2期

刘竹琴，刘艳峰

（延安大学物理与电子信息学院，陕西延安 716000）

杨氏模量是选定机械零件材料的依据之一，也是工程技术设计中常用的参数，杨氏模量的测定对研究金属材料、聚合物、陶瓷、半导体、光纤材料、纳米材料、橡胶等各种材料的力学性质有着重要意义，因此各高等院校普遍开设这一实验项目［1－6］。杨氏模量的测量方法主要有拉伸法［7－8］和振动法［9－11］，但对于非线型固体（如金属棒）则无法利用拉伸法进行测量。为了拓宽杨氏模量的测量方法，本文中利用超声波测试仪测量非线型固体的杨氏模量。

1 实验装置

本实验所涉及的实验仪器及实验材料包括：杭州大华生产的SVX－5 型信号发生器、示波器、SV－DH－7A 型声速测定仪、物理天平、游标卡尺、耦合剂、样品棒及待测样品。SV－DH－7A 型声速测试仪可用来观察、研究声波在不同介质中的传播现象，是测量介质中声波的传播速度的专用仪器。图1是实验装置图。

图1 实验装置图

2 实验原理

声波是一种频率介于20 Hz～20kHz的机械振动在弹性介质中激起而传播的机械纵波。把频率低于20Hz的机械纵波称为次声波，频率超过20kHz的机械纵波称为超声波。超声波具有波长短、易于定向发射等优点。声速实验所采用的声波频率一般都在20～60kHz之间，在此频率范围内，采用压电陶瓷换能器作为声波的发射器，接收效果最佳。

2.1 时差法测量声速

图2为时差法测量声速实验装置原理图。时差法测量声速通常指的是让连续波经脉冲调制后由发射换能器发射到被测介质中，超声波在介质中传播，经过t的时间后，到达距离l处的接收换能器。由运动学知识可知，声波在该介质中传播的速度可由以下公式求出：

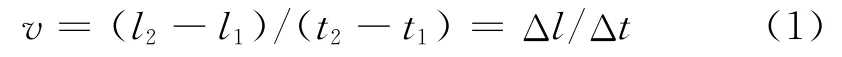
其中，v代表超声波在介质中的传播速度，t1代表声波传到l1处所用的时间，t2代表声波传到l2处所用的时间。通过测量两换能器（S1和S2）的发射平面与接收平面之间的距离和时间后，就可以计算出当前介质下的声波传播速度。测量之时，将样品棒固定在发射端与接收端换能器之间，使两换能器的端面和固体样品棒对准并紧密接触，调节接受增益，使显示的时间差值稳定，此时仪器内置的计时器工作在最佳状态。通过仪器自带的电子游标卡尺读出距离。为得到准确的结果，接触面都涂上适量的耦合剂。

图2 时差法测量声速实验装置原理图

2.2 杨氏模量公式

固体中弹性纵波的波速为［12］

式中，Y 为待测固体的杨氏模量，ρ 为待测固体的密度。因此有

式中Δl为待测固体长度。

3 实验方法

（1）按照图2连接好仪器，在仪器使用之前，打开电源开机预热15min，将测试方法设置为用脉冲波方式，并选择大脉冲波强度。

（2）将长度为l1的铝棒（也可是其他材料）固定在发射换能器与接收换能器之间，在接触面处涂上医用耦合剂，使两换能器的表面和固体样品棒的两侧紧密接触并且对准，适当调节好接收增益，使所显示的时间读数稳定，此时仪器内置的电子计时器工作状态为最佳。记录此刻信号源计时器所显示的时间t1值，通过声速测试仪上的电子游标卡尺读出距离l1。

（3）将待测固体棒接触面上涂上的耦合剂，夹在样品棒和换能器之间，使换能器的端面、待测固体棒及长为l1的铝棒对准并使其紧密接触，观察并记录这时信号源计时器所显示的时间t2，则超声波通过待测固体棒所用的时间为Δt＝t2－t1。通过声速测试仪上的电子游标卡尺读出此时的距离l2，则超声波通过待测固体棒的长度为Δl＝l2－l1。

（4）依次改变待测固体棒的长度，重复上述操作。

4 测量举例

（1）测量待测固体棒的密度。选用实验室现有的铝棒作为待测固体，在实验室正常的温度和湿度下，测得其密度为2.68g／cm3。

（2）用时差法测量声速。依次改变待测固体的长度，用时差法测声速，测量数据见表2。l1＝99.67cm，t1＝67μs。

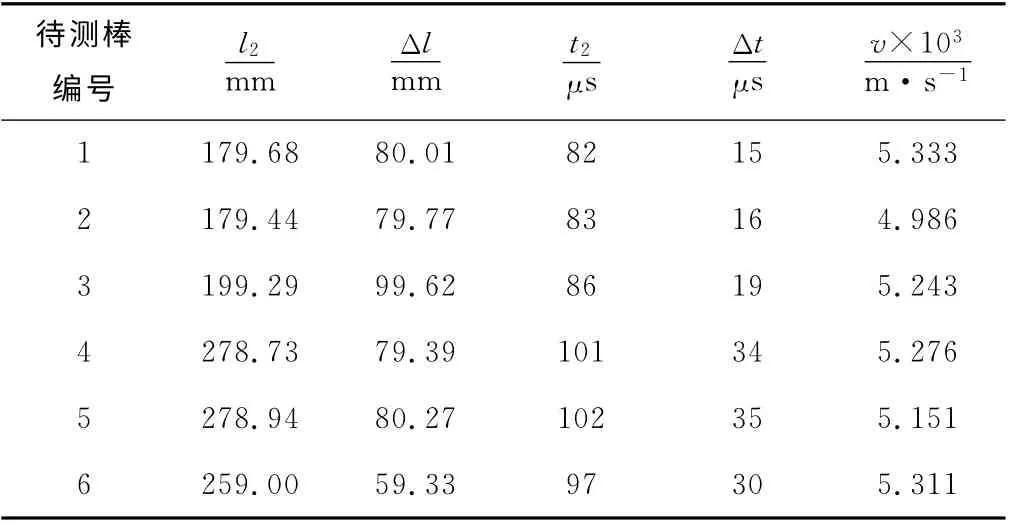
表2 时差法测量声速数据

超声波通过铝棒的传播速度平均值为5.216×103m／s。铝棒的杨氏模量为7.29×1010N·m－2。铝的杨氏模量标准值［7］为7.03×1010N·m－2，测量结果与标准值相比，其相对误差为3.7%。

5 结束语

本文中利用时差法测量超声波在非线型固体中的传播速度，进而得到待测物质的杨氏模量。测量原理简单，方法可行。从相对误差来看，此方法测量固体材料的杨氏模量误差较小，是一种测量非线型固体材料杨氏模量的简便方法，具有推广价值。超声波法测量固体材料的杨氏模量，克服了传统实验方法无法测量非线型固体杨氏模量的缺点，拓宽了固体杨氏模量的测量方法，也激发和培养了学生的创新能力和创新意识。

（

）

［1］牛晓东，袁小燕，郭嘉泰.拉伸法测钢丝杨氏模量中钢丝直径减小对测量结果的影响［J］.实验室科学，2012，15（2）：81－84.

［2］万伟.拉伸法测杨氏模量的改进［J］.西南科技大学学报，2009，24（2）：92－94.

［3］姬忠涛，王连友，陶淑芬.利用激光测量金属丝杨氏模量的实验研究［J］.曲靖师范学院学报，2008，27（6）：49－52.

［4］孔维姝，唐延林，胡林.杨氏模量实验仪器调节的一种优化方法及实施方案［J］.大学物理，2010，29（11）：37－39.

［5］黄增光，马再超，卢佃清，等.衍射法测金属丝的杨氏模量［J］.物理与工程，2008，18（5）：27－29.

［6］徐嘉彬，袁海甘，吴鸿斌，等.弯曲共振法测量材料的杨氏模量实验改进［J］.物理实验，2011，31（11）：43－46.

［7］杨述武.普通物理实验：力学、热学部分［M］.4版.北京：高等教育出版社，2007：48－51，193.

［8］刘竹琴，杨能勋.大学物理实验教程［M］.北京：北京理工大学出版社，2012：111－113.

［9］余观夏，林扬帆.振动法同时测定动态杨氏模量和剪切模量［J］.物理实验，2011，31（3）：1－3.

［10］蒋首超，彭航.弯曲共振法测量金属材料高温弹性模量探讨［J］.实验技术与管理，2011，28（4）：36－38.