基于模糊数学的滨里海盆地东南油气储层评价

朱 伟，顾韶秋，曹子剑，张国一

(1. 湖南科技大学土木学院，湖南湘潭，411201; 2. 中国石油吉林油田勘探开发研究院，吉林松原，138000)

模糊数学是引用隶属函数的概念建立的数学体系，隶属函数可以用［0，1］区间内的任意值来描述一个对象是否属于该集合，不仅仅局限于精确函数那样取1(属于)或0(不属于)。因此隶属函数具有描述事物渐变过渡的能力。模糊数学在承认数学的精确性的同时，向模糊性逼近。由于模糊数学具有不确定性，同时还能确定事件的发生与否，在面对复杂地质情况时具有综合评判优势［1-2］。前人在油气成藏地质评价中尝试过多种方法，比如关联分析法、神经网络法、随机建模法等［3-5］。与这些方法相比，模糊数学方法在研究含油气性中诸多不确定影响因素方面具有优势，因此曾广泛用在圈闭地质评价中［6］。模糊数学方法可以使人们更客观评价油气藏［7-11］。而油气储层评价又是油藏评价中最重要和复杂的因素，通常对储集层的含油气性难以作出十分精确的评价。本文在前人研究基础上，应用模糊数学方法开展了储集层油气评价，采用判别一个对象对某个概念的隶属程度，然后采取择优原则及聚类分析、综合评价等方法，挑选隶属程度高的，筛去隶属程度低的对象，运用连续多值逻辑就可以充分利用精度有限的数据所提供的信息，可以获得较客观的结论。

图1 滨里海盆地构造区划及研究区位置Fig.1 The Pre-Caspian Basin structure division map and location of the study area

哈萨克斯坦滨里海盆地地处东欧地台东南部边缘为克拉通边缘前陆盆地，与中里海盆地、南里海盆地、卡拉库姆盆地和北乌斯纠尔特盆地同为里海地区的主要含油气区(图1)。滨里海盆地是世界上沉降最深的盆地之一，巨厚的古生界、中生界和新生界的沉积物充填了盆地。从古生界、中生界到新生界，分别经历了海相、海陆过渡相和陆相沉积为主的演变［12］。

1 有利油气成藏组合及圈闭

该区烃源岩分为盐上层系烃源岩和盐下层系烃源岩。盐上地层盐丘上拱构造区的地层，因二叠系孔谷组巨厚盐层上拱构造活动埋藏浅，破坏了古温度热场，有机质一般达不到成熟条件，因此不具备大量生成液态烃的条件。盐上储层中的原油大部分来自于盐下生油层，盐上层系三叠系生油岩已成熟可提供一定量的油气，侏罗系广泛发育的泥页岩沉积具备生油的物质条件，具有一定的有机质丰度且有机质类型为Ⅱ1型，关键是有机质的成熟度是否达生油门限的热演化条件。研究表明，不同地区盐上源岩在时代和岩性上是有差别的［13］。

侏罗系在盆地内不同地区的热演化史、构造演化史、沉积埋藏史等是不同的，该地区的盐丘分布较多，侏罗系因二叠系盐层上拱构造活动导致不同的地质构造，因此所经历的热演化过程有较大的差异性。成为盐下泥盆系和石炭系生烃向上纵向阶梯式运移至盐上中生界成藏的通道。

该区盐上组合中圈闭发育广，类型多，有利于油气圈闭条件良好［14］。孔谷组盐层在三叠纪末和古近纪发生盐体上拱底辟作用，刺穿构造活动具有重要影响，在该区块形成了断层圈闭。按圈闭特征来划分，形成了背斜型、断层型、断层与背斜组合型油气藏类型，背斜多为穹窿型，断鼻构造也常见。区块为披覆在盐株状盐岩构造上的背斜隆起，其轴部呈近南北向分布。背斜北部延伸至工区以外，南部被近东西向发育的两个断层F1、F2所切割，西翼地层倾角比东翼稍陡，倾角为3°～6°，西侧盐上三叠系、中侏罗系加厚，易形成地层岩性圈闭，使油气聚集成藏。

2 储层物性

盐上层系中三叠统、侏罗系和白垩系的陆源碎屑储集层在全盆地都有较好发育。沉积环境为浅海陆棚相、海滩砂坝相和三角洲相，储集层物性较好，分布层位多。根据纵向岩性组合和旋回特征可将本区储集层划分为四个砂层组，分别是J2Ⅰ砂层组、J2Ⅱ砂层组、TⅠ砂层组、TⅡ砂层组、TⅢ砂层组。

上三叠统物性较好的砂岩储层连通性较差，即使同一构造带内各次级隆起与凹陷区内的储集层的分布与性质因局部构造和沉积不同，有明显的差异性(表1)。

表1 滨里海盆地上三叠统储层物性Table 1 Reservoir physical properties of the Upper Triassic in the Pre-Caspian Basin

根据测井数据分析，该区盐上储集层主要为中侏罗统和中、下三叠统粉砂岩和砂岩。中侏罗统以陆相、过渡相和浅海陆棚相为主，储集层主是要砂岩和粉砂岩。下白垩统、中侏罗统和三叠系是滨里海盆地盐上层系油气田的主要产层，其物性测井解释结果与容积法储量结果见表2。

根据本区块有效厚度下限标准，对本区20 口井进行了储集层的划分和定性、定量解释。盐上主力油气层中侏罗统的孔隙度为10%～20%，渗透率为0.5 ×10-3～6 000 ×10-3μm2;三叠系孔隙度为17%～20%;渗透率则变化较大，变化范围从小于1 ×10-3μm2到900 ×10-3μm2以上。储层总体上表现为中孔-中、高渗型，局部为中孔-低渗型。储层主力层J2Ⅱ油藏平均原始地层压力为24.8 MPa，平均饱和压力为6.15 MPa，地层温度为69.8～78.9 ℃;主力层TⅡ油藏平均原始地层压力28.6 MPa，平均饱和压力2.6 MPa，地层温度为73.0～76.9 ℃。

储层非均质性从平面非均质性、层间非均质性及层内非均质性来分析［15］。以储层测井二次解释结果为基础，通过孔隙度、渗透率在平面的变化及砂体连通情况等分析，本区砂体厚度较大的部位相应的孔渗物性较好，砂体连通性较好，非均质性程度中等。

盐上组合一般具有很好的盖层条件，下三叠统-上三叠统的厚层泥页岩达到了有效厚度，有效的封盖和保存了储层中的油气［16］。各油气区的盖层主要是页岩，但受构造及沉积环境影响，分布层位存在差别。滨里海盆地下二叠统孔谷组巨厚盐层的构造运动，使上覆储层形成了大量有利的圈闭。如背斜褶皱型圈闭、盐株刺穿遮挡型圈闭、断裂型圈闭及各种组合型等。盆地内广泛发育的下二叠统孔谷组含盐厚层对盐下层的油气有很好的区域性封闭和遮挡作用。构造运动导致在局部地区含盐层系的孔谷组盐层底辟变形，使得盐下层系的油气沿断裂通道运移到上覆地层的盐上层系，形成盐上油气藏。

3 模糊数学评价

模糊数学在承认数学精确性的同时向模糊性逼近。正因为模糊数学具有不确定性，而同时还能确定事件的发生与否，模糊数学可以从已知圈闭中完善权重的集合，改善因素的隶属关系，预测有利圈闭［17-25］。油气藏自身所具有的不确定性，以及模糊数学可以克服常规含油气性及其优劣程度评价过程中许多不定因素带来的诸多不便，因此圈闭或有效储层地质评价时模糊数学综合评判法被广泛应用。模糊数学方法使人们更客观评价油气藏。

表2 滨里海盆地J2Ⅰ—TⅡ储层物性参数及储量统计Table 2 Reservoir parameters and reserve statistics of J2Ⅰ-TⅡreservoirs in the Pre-Caspian Basin

3.1 模糊数学原理

根据模糊数学原理可以建立综合评级模型［22-25］如下所示。

设模糊集W 为论域U 因素的子集合:

设模糊集E 为论域V 评价级模糊子集:

模糊矩阵E=(eij)nm(i =1，2，…，n;j =1，2，…，m)，其中eij为第i 个因素的第j 个因子。其综合评价模型公式如下:

A=(a1，a2，…，am)为模糊综合评价的结果;W 为U 中各因素对评价的影响程度，分别赋予不同权重所组成的模糊子集;E 为地质因素的隶属度值模糊关系矩阵。

3.2 模糊关系权值计算模型

在建立了模糊关系矩阵R 和权值矩阵A 后，根据模糊变换原理求出模糊矩阵A=WE，其中A=(a1，a2，…，am)。对W 和E 取具有计算模型M(·，⊕)即加权平均型。

3.3 地质因素模糊体系的建立

开展模糊评价首先要建立地质因素模糊体系。根据油气成藏过程中圈闭中各要素的重要程度，将该区地质因素分为静态因素生油岩、储层、圈闭、盖层、封闭条件以及动态因素运移聚集、时空匹配等。

对于多个地质因素，首先采用多元逐步回归分析法，解决3 个地质问题。

1)确定相关关系:地质储量y 与其他地质因素xi(i=1，2，…，p;p≤n)，如果y 与xi存在相关性，则表示出y 与xi相关性的数学表达式。

2)以xi(i=1，2，…，p;p≤n)的观测值为基础，据已明确的相关性表达式初步预测储量y 的估计值，并可以进行计算结果的误差验证。

3)通过多元回归分析方法可以找出对y 作用大的地质因素，排除对y 的作用小的非关键因素，进而简化地质模型中各个因素的研究。

若储量y 与xi(i =1，2，…，n)之间可以找出下述表达式:

即变量y 与xi(i =1，2，…，n)之间具有n 元线性相关关系，简称为n 元线性关系，并称式(5)为n 元线性回归模型，其待定系数为a1，a2，…an，误差项为ε-N(0，σ2)。且将现在已经掌握的地质因子的数据代入公式(5)计算，根据收集到的数值，再根据最小二乘法，求解偏差平方组，就可以确定待定系数的最佳估计值(b0，b1…，bm)，也就是回归系数，得到的线性回归方程式:

进而可以得出，哪些地质因子是对油藏的中含油面积形成起着重要的作用。据此采用计算机编程实现多元线性回归分析，采用模糊数学的阀值0.01，小于0.01的变量，从众多的储量地质因素中剔除，最终确定了含油面积、孔隙度、含油饱和度、原油体积系数、密度、平均有效厚度作为评价储层的地质因素集合。

3.4 模糊评价步骤

该区块紧邻普罗尔瓦区块群，其上油层属于二叠系-三叠系和中、上侏罗统。该储集层沉积相为陆棚过渡相，具有较好的储集条件。对储层进行综合评价因素的定量化，首先要对这些因素的各种定性概念进行量化处理。量化的过程实际就是确定隶属函数，求得各储层评判因素的隶属度。根据专家评价法、以及其他相关的石油地质规范评价给出的隶属度函数，确定地质要素的隶属度。

1)储层含油面积

砂体发育好，是油气成藏的一个必要条件。在评价储集层时，含油面积的大小，对储层的评价起了非常重要的作用。储层的含油面积隶属度函数A(s)采用下式:

其中:sm为最大含油面积，km2;s 为含油面积，km2。

2)储层厚度

储层厚度h(m)隶属于有利储层的隶属度函数U(h)，

式中:a 是储层为有效厚度的临界值，a =0.2;b 为正数，b=10。

3)储层孔隙度

在实际生产中，孔隙度(Φ)按如下方式分级。

碎屑岩:Φ≥30%特高孔

25%≤Φ ＜30%高孔

15%≤Φ ＜25%中孔

10%≤Φ ＜15%低孔

5%≤Φ ＜10%特低孔

Φ ＜5%超低孔

碳酸盐岩:Φ≥20%高孔

12%≤Φ ＜20% 中孔

4%≤Φ ＜12%低孔

Φ ＜4%特低孔

采用储集岩孔隙度隶属度函数y(Φ)，求得孔隙度的隶属度(表3)。

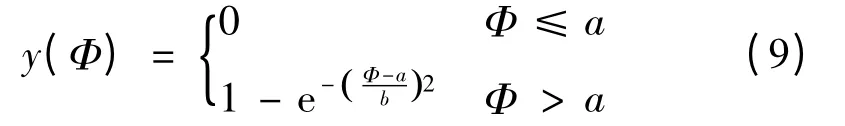
式中:a 为碎屑岩的低孔隙度值，a = 10;b 为正数，b=8。

4)储层含油饱和度

储集岩含油饱和度的隶属度函数

其中，各变量的对应取值据公式经验值和实验测定数据:a=0.88(侏罗系)，1.00(三叠系);b =1.00(侏罗系和三叠系);m =2.03(侏罗系)，1.87(三叠系);n =2.03(侏罗系)，1.88(三叠系);Rw=0.02(侏罗系和三叠系);Rt为测井曲线电阻率。根据上式和该区块测井曲线的电阻率，得出含油饱和度隶属度。

5)原油体积系数

依据图2 中各个变量之间的关系，由下式求得原油体积系数隶属度:

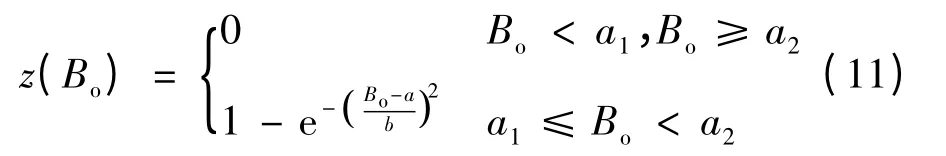
其中，Bo为原油体积系数;a1，a2根据图2 取原油体积系数极值，a1=0.9，a2=1.34;b 是经验值，b=0.2。

3.5 模糊评价结果

设权重为W =(w1，w2，…，wn)＇，其中w1，w2，…，

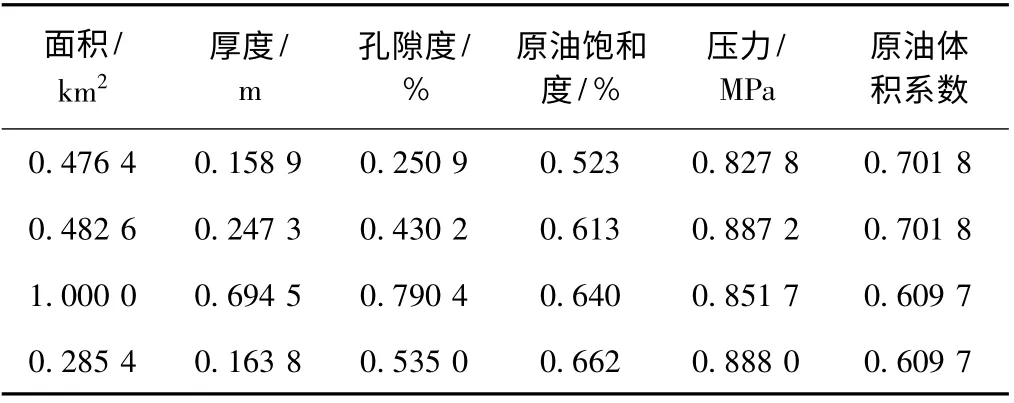
表3 滨里海盆地地质因素隶属度值Table 3 Membership values of geological facters in the Pre-Caspian Basin

图2 滨里海盆地地下原油体积系数(Bo)、粘度(μo)与压力(p)关系Fig.2 Relationship between oil volume factors (Bo)，viscosity (μo)and pressure (p)in the Pre-Caspian Basin

表4 滨里海盆地储层模糊数学综合评价Table 4 Comprehensive reservoir evaluation with fuzzy mathematics in the Pre-Caspian Basin

在Matlab 中，基于上面的隶属度，组成模糊关系矩阵E，结合研究区的地质特征，采用专家打分法，给出权重值为W =(0.2，0.2，0.2，0.2，0.15，0.05)＇，进行模糊数学综合运算，得到了各个地质因素面积(s)、储层厚度(h)、孔隙度(Φ)、原油饱和度(So)和原油体积系数(Bo)的隶属度值(表3)。

结合模糊数学的综合运算，得出的综合评价结果勘探揭示:根据本区块建立的模糊数学综合评价模型，加权平均型求得的综合评价更为客观，结果贴近实际，确定了权重值取得的可行性(表4)。

4 结论

采用模糊数学方法，结合多元回归分析法，最小二乘法用计算机编程运算，优化了储层评价地质参数体系，找到了关键地质因素。建立了一个有效的基于模糊数学的储层评价量化模型。通过多个模糊模型的对比和定量计算，得到了储层评价综合排序，确定了J2Ⅱ和TⅡ储层为本区优势储层，储油能力最强。该储层为中孔-中、高渗型，中孔-低渗型储层，有较好的油气来源，具备油气成藏的储层条件。

［1］赵鹏大. 试论地质体的数学特征［J］. 地球科学，1982，16(1):145-155.Zhao Pengda.On the mathematical characteristic of geological bodies［J］.Earth Science，1982，16(1):145-155.

［2］赵鹏大.地质勘探中的统计分析［M］. 武汉:中国地质大学出版社，1990.Zhao Pengda. Statistical analysis in geological exploration［M］. Wu han:China University of Geosciences Publisher，1990.

［3］侯瑞云.大牛地气田盒一段低孔渗砂岩储层特征［J］. 石油与天然气地质，2012，33(3):467-478.Hou Ruiyun.Reservoir characteriseics of low porosity and permeability sandstone of Member Ⅰof Xiashihezi Formation in Daniudi gas field［J］.Oil ＆ Gas Geology，2012，33(3):467-478.

［4］李东安，宁俊瑞，刘振峰. 用神经网络和地质统计学综合多元信息进行储层预测［J］. 石油与天然气地质，2010，31(4):493-503.Li Dongan，Ning Junrui，Liu Zhenfeng.Reservoir prediction with integrated information based on artificial neural network technology and geostatistics［J］.Oil ＆ Gas Geology，2010，31(4):493-503.

［5］崇仁杰，于兴河，李婷婷. 应用实验设计优选随机建模的储层模型［J］.石油与天然气地质，2012，33(1):94-101.Chong Renjie，Yu Xinhe，Li Tingting.Application of experimental design theory in stochastic reservoir model optimization［J］.Oil ＆ Gas Geology，2012，33(1):94-101.

［6］许多年，王伟锋.模糊综合评判技术在乌夏地区圈闭评价中的应用［J］.新疆石油天然气，2006，2(4):7-11.Xu Duonian，Wang Weifeng.Fuzzy comprehensive judgement to evaluate the Triassic traps in Wu-Xia area［J］. Xinjiang Oil ＆ Gas，2006，2(4):7-11.

［7］孟艳军，汤达祯，许浩. 煤层气产能潜力模糊数学评价研究——以河东煤田柳林矿区为例［J］.中国煤炭地质，2010，22(6):17-20.Meng Yanjun，Tang Dazhen，Xu Hao.CBM potential productivity assessment through fuzzy mathematics—a case study in Liulin mine area，Hedong coalfield［J］. Coal Geology of China，2010，22(6):17-20.

［8］李爱国，易海永，陈忠. 模糊数学在渝东地区石炭系圈闭评价中的应用［J］.天然气工业，2003，23(4):23-26.Li Aiguo，Yi Haiyong，Chen Zhongfu.Application of fuzzy mathematics in evaluating the carboniferous traps in east Chong Qing［J］.Natural Gas Industry，2003，23(4):23-26.

［9］Finol J J，Guo Y K，Jing X D.Fuzzy partitioning systems for electrofacies classification［J］.Petroleum Geology，2001，24(4):441-458.

［10］唐庆宝.应用模糊数学方法评价局部圈闭［J］. 石油地球物理勘探，1985，20(5):490-495.Tang Qingbao.Evaluating oil trap by fuzzy mathematics［J］.Oil Geophysical Prospecting，1985，20(5):490-495.

［11］伊广林.在储集层油气评价中模糊数学的应用［J］. 测井技术，1982，(4):20-29.Yi Guanglin.The application of fuzzy mathematics in reservoirs evaluation［J］. Well Logging Technology ，1982，(4):20-29.

［12］钱桂华.哈萨克斯坦滨里海盆地油气地质特征及勘探方向［J］.中国石油勘探，2005，10(5):60-66.Qian Guihua.Oil-gas geological features and its exploration direction in marginal Caspian Basin，Kazakhstan［J］.China Petrleum Exploration，2005，10(5):60-66.

［13］刘洛夫，朱毅秀，张占峰，等.滨里海盆地盐上层的油气地质特征［J］.新疆石油地质，2002，23(5):442-448.Liu Luofu，Zhu Yixiu，Zhang Zhan Feng，et al. Hydrocarbon geologic characteristics of up-salt zone in Caspian Seashore Basin［J］. Xinjiang Petroleum Geology，2002，23(5):442-448.

［14］史丹妮，杨双.滨里海盆地盐岩运动及相关圈闭类型［J］.岩性油气藏，2007，19(3):73-79.Shi Danni，Yang Shuang.Salt movement and the types of related traps in Pre-Caspian Basin［J］. Lithologic Reservoirs，2007，19(3):73-79.

［15］王亮，牛成民，杨波，等.莱州湾凹陷沙三段含油气系统与有利勘探方向［J］.断块油气田，2011，18(5):545-548.Wang Liang，Niu Chengmin，Yang Bo，et al.Petroleum sysem and favorable exploration targets of the third member of Shahejie Formation in Laizhouwan Depression［J］.Fault-Block Oil＆Gas Field，2011，18(5):545-548.

［16］张建球，米中荣，周亚彤，等.滨里海盆地东南部盐上层系油气运聚规律与成藏［J］.中国石油勘探，2010，15(5):56-62，80.Zhang Jianqiu，Mi Zhongrong，Zhou Yatong，et al.Oil and gas migration and accumulation ＆ reservoir formation in post-salt strata in Southeast Pre-Caspian Basin［J］. China Petroleum Exploration，2010，15(5):56-62，80.

［17］Ishibuchi H，Nakashima T，Murata T. A fuzzy classifier system that generates fuzzy if-then rules for pattern classification［J］. IEEE，2001，77(6):759-764.

［18］Dubois D，Prade H. Fuzzy sets and systems theory and application［M］.New York:Academic Press，1978.

［19］Dubois D，Prade H. Fuzzy sets in approximate reasoning［J］. Fuzzy Sets and Systems，1991，40(1):143-244.

［20］Wong P，Aminzadeh F，Nikravesh M. Soft computing for reservoir characterization and modeling［J］.Studies as fuzziness and soft computing，2001，80(5):586-590.

［21］Deluca A，Termini S. A definition of nonprobabilistic entropy in the setting of fuzzy sets theory information and control［J］.1972，20(4):301-302.

［22］王翠香.模糊集合的模糊度的一种表示形式［J］. 数学的实践与认识，2006，36(2):267-269.Wang Cuixiang. The analytic expressions of the degree of fuzziness about fuzzy sets［J］. Mathematics in Practice and Theory，2006，36(2):267-269.

［23］杨凯.模糊数学在矿山环境影响评价中的应用［J］. 四川环境，2010，29(3):127-130.Yang Kai. Application of Fuzzy mathematics in mine environmental impact assessment［J］. Sichuan Environment，2010，29(3):127-130.

［24］伊广林.在储集层油气评价中模糊数学的应用［J］. 测井技术，1982，(4):20-29.Yi Guanglin. The application of fuzzy mathematics in the reservoir evaluation［J］.Well Logging Technology，1982，(4):20-29.

［25］李鸿吉. 模糊数学基础及实用算法［M］. 北京:科学出版社，2005.Li Hongji. Com-fuzzy math and practical algorithm［M］. Beijng:Science Press，2005.