基于四阶积累量的卫星TDOA定位参数估计算法研究

解放军理工大学通信工程学院 张 威 张更新

总参61所通信中心 韩福春

一、 引言

随着卫星通信业务的飞速发展，卫星通信面临的电磁环境日益恶化，难以避免受到各种辐射源有意或无意的干扰，因此对辐射源进行准确的无源定位以采取有效的针对措施有着重要的意义。不同的卫星收到的同一源干扰信号之间由于传播距离不同会引起时延差，即TDOA（Time difference of arrival）。TDOA中包含了干扰源的空间位置信息。因此，准确、快速地估计和测定各卫星透明转发的干扰源信号之间的TDOA值并选取合适的定位算法，是进行干扰源定位的关键前提。

目前，传统的TDOA参数估计方法在非相关噪声环境下能够对TDOA参数进行较好的估计，但在相关噪声环境下，这些方法将不能对TDOA参数做出准确估计。考虑高阶积累量对高斯噪声的不敏感特性，能够较好的抑制相关高斯噪声，本文将对基于四阶积累量的TDOA参数估计方法进行研究。

二、信号模型

为了便于分析，设干扰源发射信号为调频信号如式（1）所示

如式（2）与（3）所示，x(t)与y(t)分别是受干扰主星与其邻星接收的地面干扰源信号

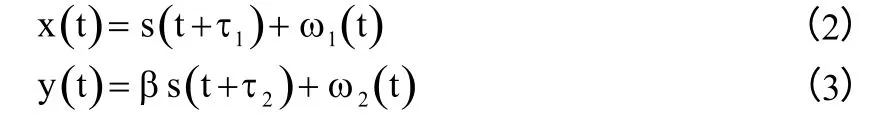
三、 算法描述

1. 广义互相关法

广义互相关TDOA参数估计方法是经典的TDOA参数估计算法，为了与基于四阶积累量的TDOA参数估计方法作对比，这里简要介绍其算法原理如下。

受干扰主星及其邻星所接收的地面干扰源信号x(t) 与y(t)的互相关函数如式（6）所示

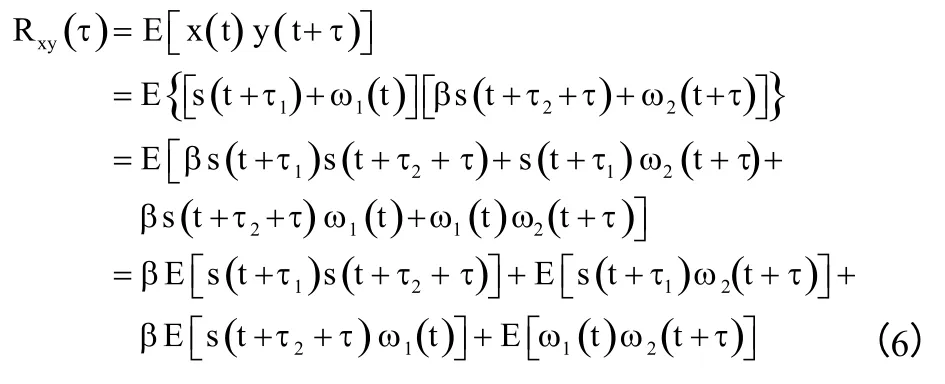
因为ω1(t)和ω2(t)为平稳、零均值的高斯噪声，且独立于s(t) ，则信号s(t+τ1)与噪声ω2(t)的互相关函数E[s(t+τ1)ω2(t+τ)]的值为0；信号s(t+τ2)与噪声ω1(t)的互相关函数E[s(t+τ2+τ)ω1(t)]的值为0；假设噪声ω1(t)与ω2(t)不相关，则ω1(t)与ω2(t)的互相关函数E[ω1(t)ω2(t+τ)]的值为0。整理（6）式可得式（7）

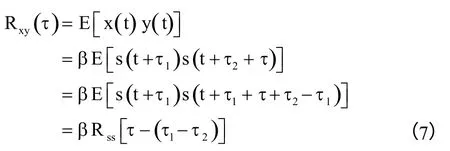
2. 基于四阶积累量的TDOA参数估计法

受干扰主星及其邻星所接收的地面干扰源信号x(t)与y(t)的四阶累积量定义如式（9）所示

由于颈椎结构差异很大，需要采用不同的单元进行模拟：皮质骨和终板采用厚度为0.5 mm的壳单元；松质骨、髓核和纤维环采用实体单元；由于韧带是纤维组织，在载荷条件下只能承受张力，故采用受拉的truss单元.完整模型共有24 961个节点，121 978个单元.如图1所示.为模拟小关节接触的复杂问题，采用无摩擦压力过盈来模拟关节之间的关系，其中初始间隙为0.5 mm.由于椎体各个部分的材料属性差异性较大，根据颈椎的解剖结构特点以及文献[5-6]，设定不同的材料属性.如表1所示.

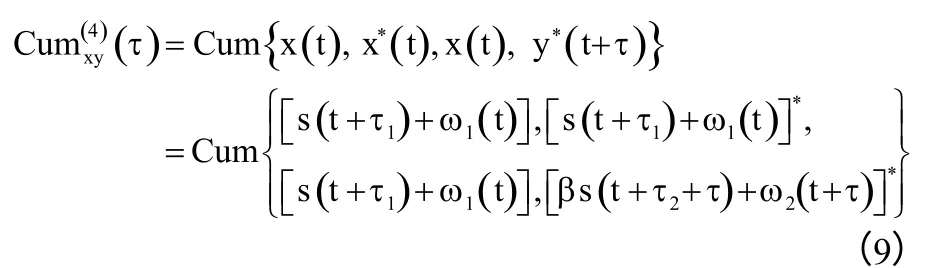
高阶累积量具有如下性质

（2）｛x1｝(i=1,2,…k)，y1为随机变量，则有

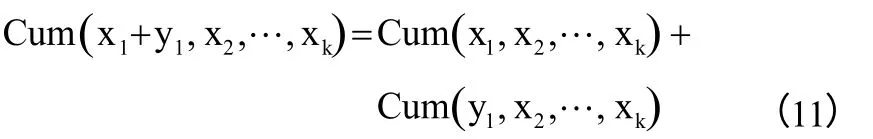
根据高阶累积量上述两种性质，又考虑ω1(t)，ω2(t)独立于干扰源信号s(t)，可由式（9）得

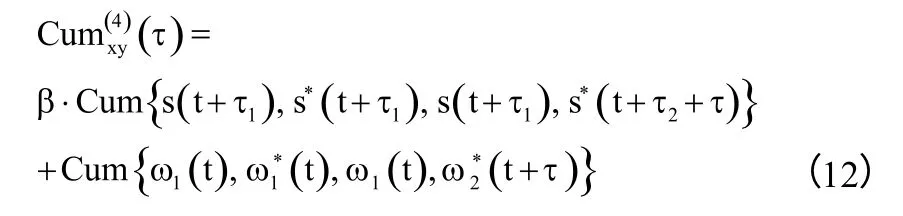
高斯噪声ω1(t)，ω2(t)的高阶累积量均为0，则由式（12）可得

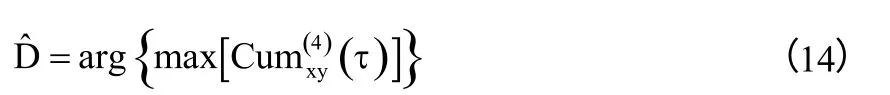
四、 仿真分析

为便于使用MATLAB进行仿真，地面干扰源信号为载波频率为fc=1.6Hz的BPSK信号，信号频率为3kHz，信号的抽样频率fs=4fc，采样周期Ts=1/fs。干扰源信号到达两颗高轨卫星分别设置为0.125s与0.135s。BPSK调制后的信号两个状态分别为s0=-1与s1=+1，且P{s0}=P{s1}=0.5。令SNR1与SNR2分别为地面接收站接收到主星和相邻卫星转发的干扰信号的信噪比，这里SNR为抽样点信号与噪声的功率之比（dB），n为仿真时BPSK基带信号码元个数，在高斯噪声的条件下对广义互相关法和基于四阶积累量的TDOA参数估计方法进行仿真。

（1） 仿真实验一

地面接收站所接收到的两路干扰源信号通过非相关高斯白噪声信道：噪声ω1(n)与ω2(n)是均值为0，方差为1的非相关高斯白噪声序列，当n=1024与SNR1=5dB固定不变，SNR2分别为0dB，-10dB，-20dB时，广义互相关法及基于四阶积累量的参数估计法对TDOA参数估计的仿真结果如下。

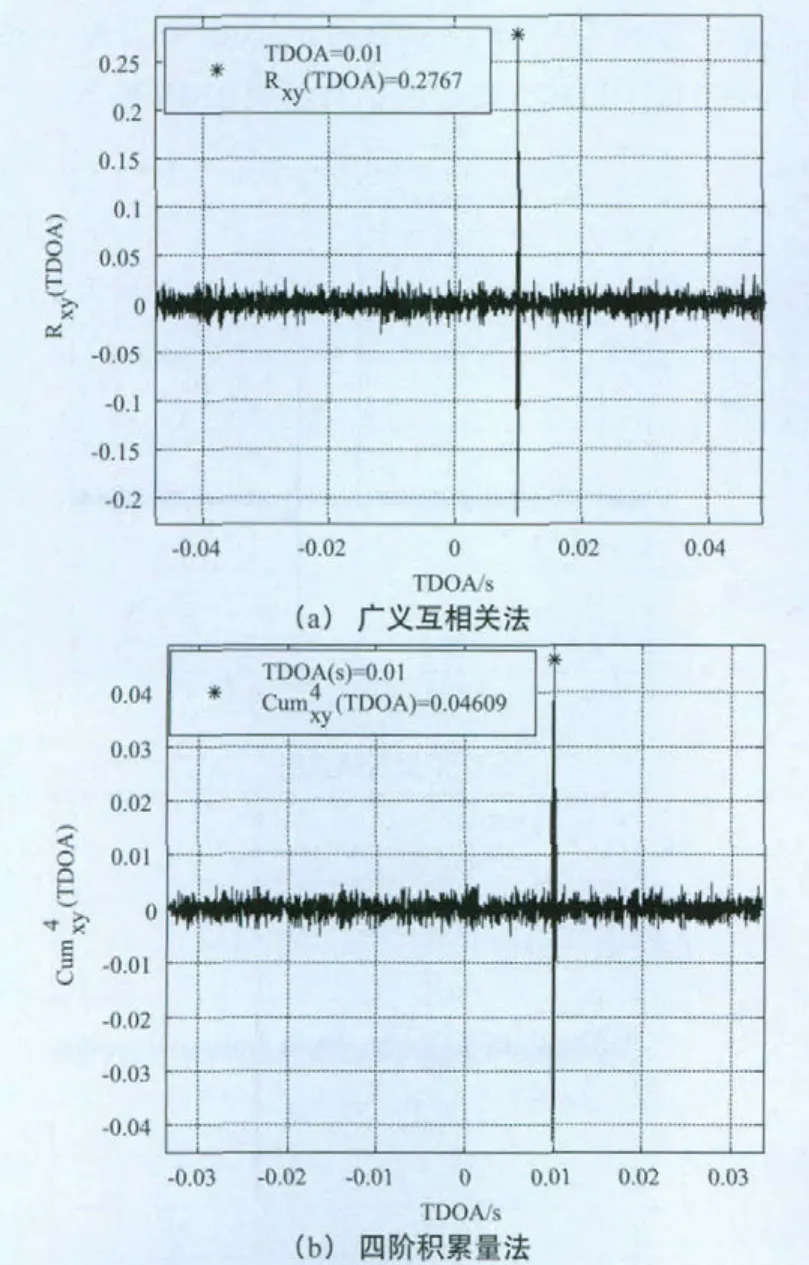
图1 TDOA参数仿真结果（SNR2=0dB ）

当n＝1204与SNR1=5dB固定不变，SNR2=-10dB时，TDOA参数的仿真结果如图2所示。

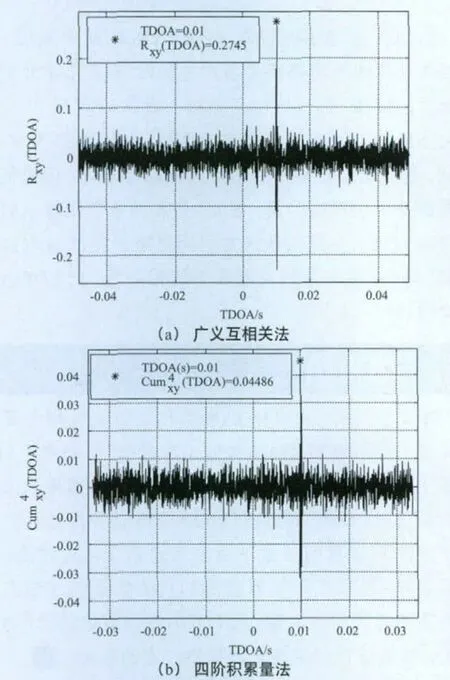
图2 TDOA参数仿真结果（SNR2=-10dB）

当n＝1204与SNR1=5dB固定不变，SNR2=-20dB时，TDOA参数的仿真结果如图3所示。

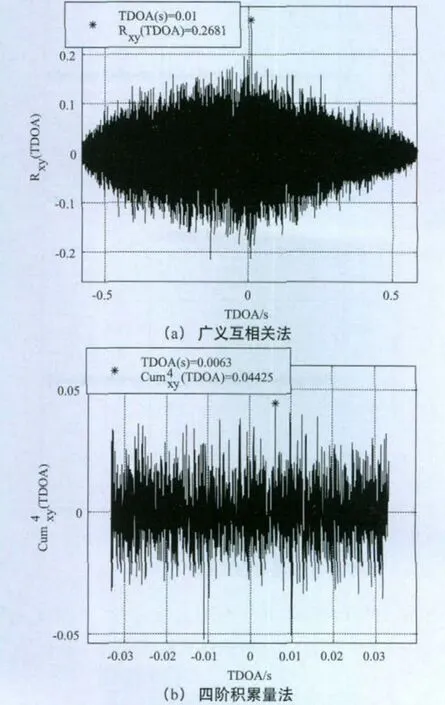
图3 TDOA参数仿真结果（SNR2=-20dB）

由仿真图1至图3可知，当n＝1204与SNR1=5dB固定不变，SNR2从0dB到-10dB时，广义互相关算法和基于四阶积累量的TDOA参数估计算法均能准确的估计出TDOA参数值；当SNR2=-20dB，广义互相关算法的估计结果中主星和其邻星接收信号的互相关峰值几乎被噪声峰值淹没，基于四阶积累量的TDOA参数估计结果也出现较大偏差。因此，在非相关高斯白噪声的信道条件下，为得到TDOA有效估计结果，需要满足SNR2＞-20dB。

（2） 仿真实验二

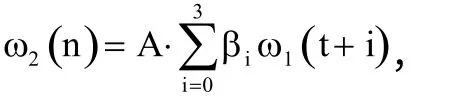
当n＝1204与SNR1=5dB固定不变，SNR2=5dB (A=1)时，TDOA参数的仿真结果如图4所示。

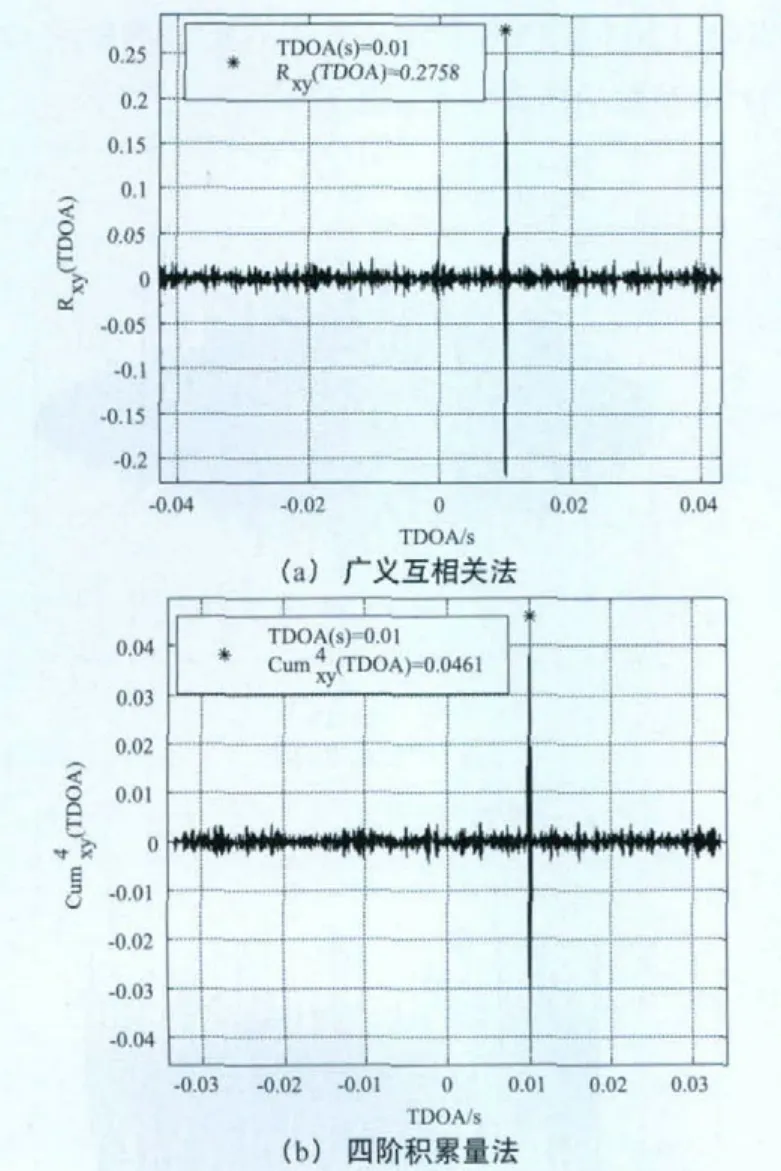
图4 TDOA参数仿真结果（SNR2=5dB）

当n＝1204与SNR1=5dB固定不变，SNR2=0dB (A=1.7783 )时，TDOA参数的仿真结果如图5所示。

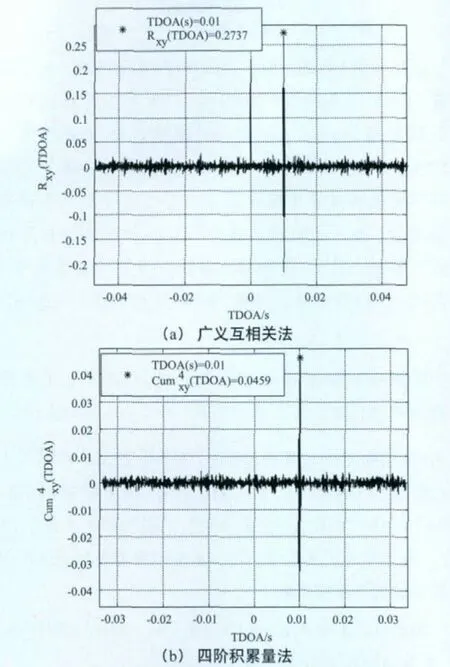
图5 TDOA参数仿真结果（SNR2=0dB）

当n＝1204与SNR1=5dB固定不变，SNR2=-5dB (A=3.1632 )时，TDOA参数的仿真结果如图6所示。

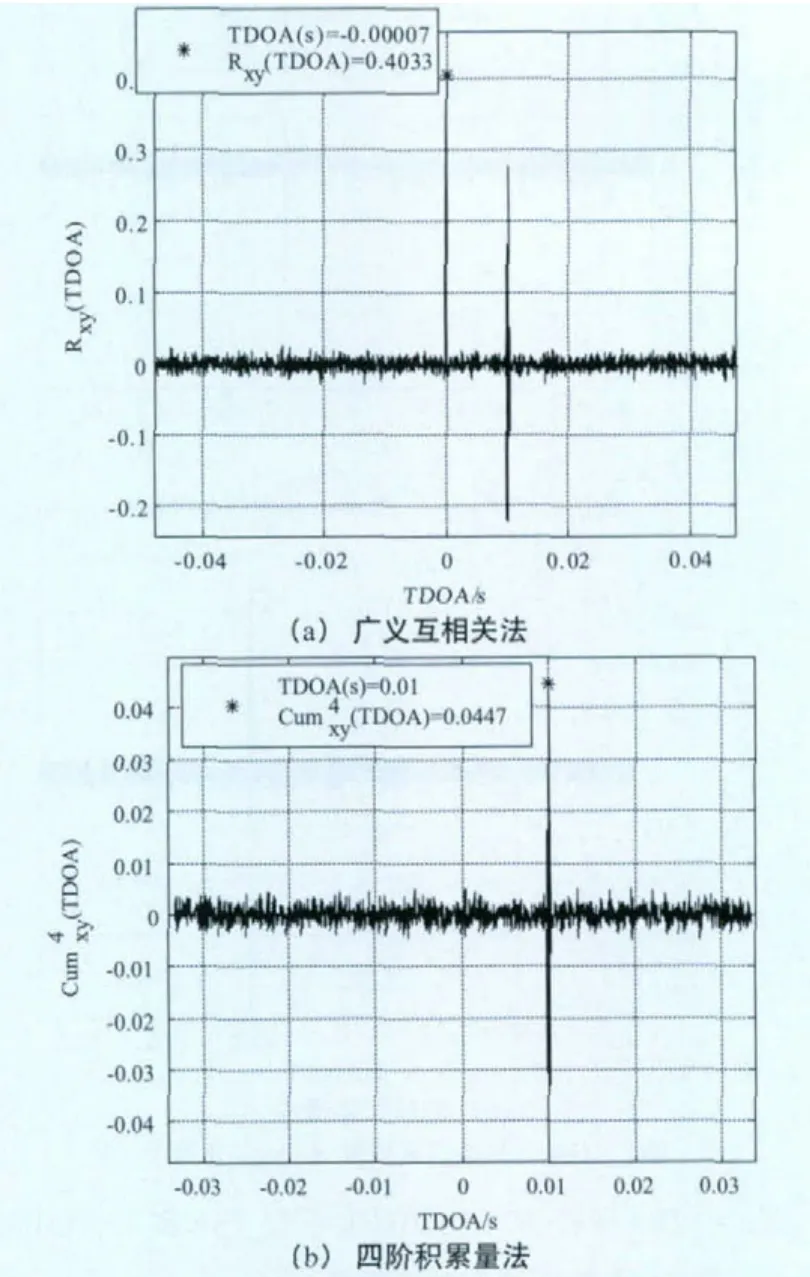
图6 TDOA参数仿真结果（SNR2=-5dB）

由仿真图4至图6可知，随着SNR2的逐渐降低，广义互相关法中由于噪声相关所产生的峰值接近或大于信号互相关的峰值，因此在相关高斯白噪声环境下，广义互相关法不能对TDOA值进行有效估计；而随着SNR2的逐渐降低，基于四阶积累量的估计效果略微变差，但信号四阶积累量峰值仍然很明显。因此，仿真结果说明基于四阶累积量的TDOA参数估计法方利用高斯过程的高阶累积量为0的特点，能有效地克服噪声的相关性，对TDOA作出有效估计。

五、 结束语

本文针对传统的TDOA参数估计方法在相干高斯噪声环境下难以对TDOA参数做出有效估计，研究了TDOA的基于四阶积累量的参数估计方法，详细推导了该方法的参数估计过程。本文将TDOA的传统参数估计方法和基于四阶积累量的参数估计方法进行了仿真对比，仿真结果表明，基于四阶积累量的TDOA参数估计法方能有效地克服噪声的相关性，对TDOA做出有效估计，为研究TDOA参数估计的相关人员提供一定的参考。

见www.dcw.org.cn