多模式驱动的机器人关节控制器设计及实验

夏 磊 范 坚 戈亦文 郝风吉 闫 雪 罗 翔

(东南大学机械工程学院,南京211189)

在机器人技术领域,作为动力源的直流电机被广泛应用于机器人各关节或执行机构中.常见的关节驱动方式大多采用直流伺服电机加减速传动装置[1],如法国的BIP2000[2]、MIT的M2[3]、日本的ASIMO[4-5]等.而直流伺服电机中最常用的是直流电机.与无刷电机与步进电机相比,直流电机具有结构紧凑、质量轻便、控制简单等特点,因此应用于很多机器人,如HRP-2[6]和BIP2000都选用了直流电机.

人类步行时,各个关节协调工作,不仅能按照预想的轨迹运动,同时还能提供所需的主动力,完成相应的动作.因此对于步行机器人的驱动关节也有同样的要求,即需要既能精确实现运动轨迹的跟踪又能提供所需的力矩.对于直流电机的驱动控制,研究者大多关注直流电机的位置控制或速度控制(即按照期望的轨迹或速度运动),并提出了很多直流电机闭环反馈调速的方法.但是,对于机器人而言,各驱动关节不仅要能实现位置控制或速度控制,完成预期的动作,很多时候还必须实现力矩控制,即让电机输出期望的力矩.比如机械手抓取物体时,手指必须施加适当的力以保证物体不会因力过小而滑落或因力过大而被挤坏.步行机器人步行时,在行走阶段,各驱动关节根据规划的轨迹,在电机位置控制模式下完成预期动作;在蹬地阶段,除了各关节协调动作以外,踝关节必须提供合适的力矩才能实现机器人的成功迈步.除此之外,很多研究者通过控制离支撑面最近的踝关节的角度和力矩来调节ZMP位置,从而保证机器人步行的稳定性[7-8].所以,驱动关节在不同条件下需要不同的控制模式.

目前在关节位置控制上,大多利用位移传感器和采用反馈调节的方法实现位置控制,如基于光电编码器的PID或模糊自适应PID位置反馈控制[9].而在力/力矩控制上,常采用力/力矩传感器以实现检测反馈[10-11].但是,这种方法往往需要检测x,y,z三个方向力和力矩,通过计算得出合力/力矩,因此比较复杂.Kong等[12]将直流电机和扭簧相结合,利用扭簧在一定范围内扭角与扭矩的线性关系,将力矩控制转化为扭角的位置控制,虽然力矩控制效果较好,但增加了结构和控制上的复杂性.

针对现行的机器人关节驱动控制的特殊要求,本文设计了具备位置控制和力矩控制功能为一体的关节控制器,并研究了这2种模式的切换控制方法.通过仿真和实验结果可以看出,所设计的控制器具备位置控制与力矩控制功能,且二者间能稳定切换.

1 系统建模与控制方法

1.1 控制理论与系统建模

机器人运动时,通过对驱动关节的控制可实现机器人按照预期的规划完成相应动作.机器人关节控制主要是对关节驱动电机的控制.关节位置控制是对电机的转角进行控制,以按照期望的转角完成相应的轨迹运动.而考虑到直流电机的驱动力矩与通过电机的电流成正比,所以关节力矩控制是对通过电机的电流进行控制,实现电机输出期望转矩.

本文提出的关节位置控制与力矩控制,建立在直流电机的数学模型上.

由经典的直流等效电路[13]可得到在零初始条件下的电压与电流的传递函数,以及电流与反电动势的传递函数，即

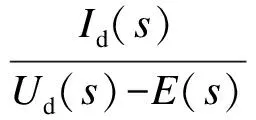
(1)

(2)

式中,Id为回路的电枢电流；E为反电动势；Tl=L/R为电枢回路的电磁时间常数，R为直流电机电枢电阻,L为回路的总电感;IdL=TL/Cm为负载电流,TL为电机的负载转矩，Cm为常数;Tm=JmR/(CeCm)为机电时间常数，Ce为电机常数.因此,针对位置控制与力矩控制的要求,控制变量就是模型中的转速n(s)和电枢电流Id(s).

1.2 控制方法

本文采用的控制方法是建立在PID控制思想上的.图1为设计的控制系统框图.

图1 控制系统框图

位置控制与力矩控制分别利用PID控制算法进行闭环反馈控制,以达到高控制精度和动态调节的平衡要求.但何时采用位置控制或力矩控制,则需要根据状态监测器(算法程序)实时监测和响应来完成控制模式的选择.当需要位置控制时,闭合位置反馈控制系统开关,打开力矩反馈控制系统开关;而需要力矩控制时,则闭合后者,打开前者.在位置控制与力矩控制下因控制的输入不同,其控制增益参数也不同,故在相应控制模式下需选用不同的PID参数,而PID参数需预先进行整定.

在控制模式切换中,需考虑2种切换模式：① 基于时间的切换.即在某一时刻由位置控制切换为力矩控制或由力矩控制切换为位置控制.② 基于电流的切换.即当检测电枢电流大于某个阈值时由位置控制切换为力矩控制,当检测到电流小于某个阈值时由力矩控制切换为位置控制，此方法和实际应用类似,如机械手在抓取到物体时,由于物体反作用力的作用,负载力矩增大,即驱动电机的电流随着增大,此时切换为力矩控制,一方面提供期望转矩,另一方面起限流作用,保护电机.在电机运行过程中,状态监测器根据实时判断模式切换条件来选择闭合位置控制环还是力矩控制环.

2 仿真

2.1 仿真搭建

为了验证所提出控制方法的可行性,利用Matlab/Simulink软件对直流电机数学模型采用PID控制算法进行了驱动控制系统的仿真.本文以MAXON直流电机(RE25 20W 118752)作为控制对象,在仿真时,将MAXON RE25 20W直流电机相关参数[14]代入经典数学模型中,同时根据需要加入PID控制环节、DAC延时环节、PWM驱动延时环节、ADC延时环节和反馈延时环节[13],位置控制仿真框图如图2所示.

图2 位置控制Matlab仿真框图

2.2 仿真结果

2.2.1 位置控制仿真

位置控制仿真时,期望的关节转角为一正弦信号,如图3(a)所示.由图可以看出,仿真时实际转角在PID调节下其跟踪期望转角的性能良好.

2.2.2 力矩控制仿真

力矩控制仿真时,期望电流为1 A,而负载电流IL先缓慢增加,斜率为0.2 A/s,然后在1 s时刻,负载电流突变至1 A,结果如图3(b)所示.由图可以看出,在1 s前由于负载较小,驱动电机电枢电流大于负载电流,根据动力学平衡方程,此时电机的转速会逐渐增大;而在1 s时刻,负载电流突然增加至1 A,此时在电压平衡方程、动力学平衡方程以及PID调节下,电枢电流快速响应,直到与负载电流相等,达到动力学平衡,此时电机转速维持恒定,电机输出恒定转矩.

2.2.3 位置控制与力矩控制切换仿真

位置控制与力矩控制切换仿真时,切换方法是基于时间的切换.先进行位置控制后进行力矩控制,切换时刻为1 s.位置控制时给予电机以恒定转速,即期望转角为斜坡信号,负载电流以0.4 A/s的速度线性增加.当时间运行至1 s,进行位置控制与力矩控制的切换,同时,负载电流突变至1 A.此时,期望电流为1 A,通过PID控制使电枢电流达到1 A,完成由位置控制转为力矩控制,得到电机电流、转速仿真结果如图3(c)、 (d)所示.

由图3可以看出,位置控制时,在PID调节下电机转速快速增加直至恒定值,此时电机的启动电流较大.而后在电压平衡方程及动力学平衡方程调节下,电枢电流与负载电流相等,转速维持恒定.当位置控制切换为力矩控制时,负载电流突变至1 A,在PID调节下,电枢电流快速响应,直至与负载电流相等并保持恒定.在负载突然增大至完成力矩控制调节的过程中,电机转速下降,调节完成后,电机转速维持不变.

3 控制系统软硬件设计

3.1 硬件设计

控制系统采用C8051F040作为主控制器,直流电机作为控制对象.为了实现位置控制和力矩控制,在硬件上必须实现电机的驱动和系统的反馈.所设计的硬件主要包含以下几个部分.

1) 单片机C8051F040.作为主控制器有如下功能:① 实时中断响应、控制模式切换等;② 利用单片机PCA工作在8位脉宽调制器的方式产生PWM(脉宽调制)控制信号并输出;③ 利用单片机定时器/计数器对光电编码器反馈产生的脉冲数进行计数,以监测实时位置,进行位置控制;④ 利用单片机AD转换模块,对经过放大后的反馈电流(转换成电压)进行AD转换,以监测实时电流,进行电流控制(力矩控制);⑤ 利用单片机串口、CAN通讯模块进行数据的实时采集,以便后续处理和分析.

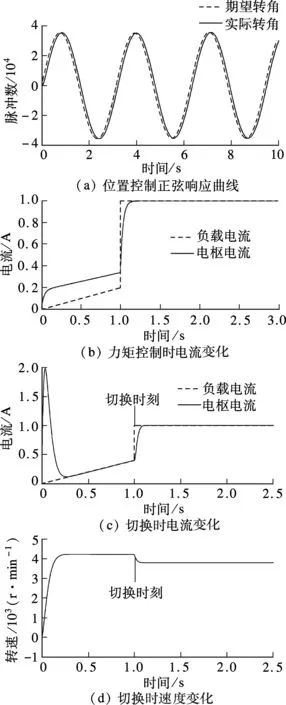
图3 Matlab/Simulink仿真结果

2) 驱动放大.采用L298N/L298P的H桥驱动电路,利用PWM信号,通过控制驱动桥三极管的通断,完成驱动电压的放大和PWM控制.

3) 直流伺服电机.实验时采用转动惯量小、控制方便的MAXON公司的直流电机(MAXON RE25 20W 118752).

4) 编码器.通过脉冲计数来精确计算位置,实时检测电机转角,反馈给单片机进行位置控制.实验时采用MAXON公司附带的HEDL-5540型、500线、三通道光电编码器,可通过比较A，B通道信号相位之间的关系来判定旋转方向.

5) 电流采样.利用电阻采样的方法,结合L298芯片电流反馈功能,对通过直流电机的电流进行实时检测并反馈,以完成电流控制(力矩控制).

6) 放大.为了提高检测精度,达到AD转换的要求,将采集到的电流信号变成微小的电压信号,并采用LM358D放大器对电压信号进行放大.

3.2 软件设计

在控制系统软件设计中,主要利用循环中断的思想.中断函数处理包括判断采用何种控制模式(位置控制或力矩控制)、设定期望转角或期望电流、增量式PID函数处理、占空比更新、AD转换完成数据处理、数据发送至PC机等.其中,最核心的部分是判断采用位置控制还是力矩控制来完成期望的动作.这部分的实现是通过定时器0溢出中断(每0.5 ms中断一次)来完成.中断响应中设定切换条件为电机电流是否达到切换阈值,若达到，则采用力矩控制,未达到则采用位置控制.当然切换条件是可以更改的,如基于位置控制可改为基于时间控制的切换.

4 实验及结果分析

实验系统采用驱动控制,该系统主要由驱动控制器、直流电流、实验装置组成.

直流电机额定转矩为26.7 mN·m,经减速比317.86的减速箱减速增扭后，与传动比1∶1的同步带传动机构的同步带轮相连,同步带传动机构另一端与负载摆臂相连.负载摆臂重力G=5.782 N,等效臂长(重心距离摆动中心距离)约0.13 m.

4.1 力矩控制验证实验

为了验证所设计的控制系统是否能够通过设定期望电流值,利用PID的力矩控制功能,进行了力矩控制的验证实验.摆臂在重力作用下位置产生不同的负载力矩为

TL=Glsinβ

(3)

式中,G为重力;l为重力臂;β为摆臂与竖直方向的夹角.

摆臂初始位置竖直向下.在程序Matlab/Simulink中,给定一个期望电流,在PID调节下,摆臂会随着驱动力矩的增加而上升,直到驱动力矩与负载力矩相等.根据电机动力学平衡方程[13],此时摆臂会停在某个角度.因此,可根据角度β、重力G、重心位置l计算出此时负载力矩的大小,即近似等于驱动力矩大小.另一方面,采用由示波器检测到的电枢电流有效值,计算出实际输出力矩与负载力矩，并对其进行比较,由此验证程序中设定的期望电流值与输出转矩的线性关系，通过实验数据拟合得到的曲线如图4(a)、(b)所示.

通过拟合的曲线可知,所设计的控制器能通过设定电流值而改变驱动力矩大小,达到力矩控制的目的.

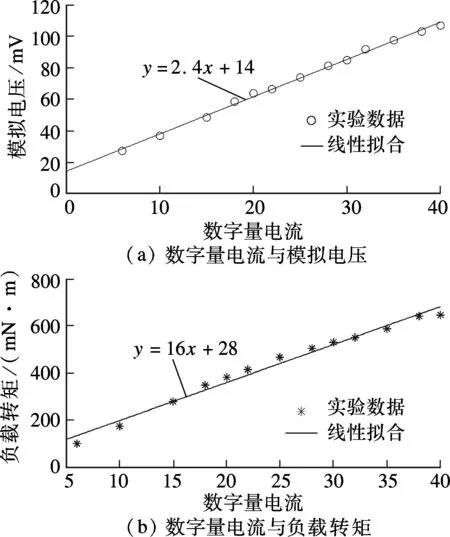
图4 电流与电压/负载转矩近似线性关系

4.2 位置控制实验

位置控制的性能主要由其对期望转角的跟踪性能决定.实验中,首先,设定期望的脉冲为一正弦信号,幅值为30 000脉冲(折算到摆臂转角约为67.95°),而周期分别为10,5,2.5和1.25 s,观察不同频率正弦信号的跟踪性能;其次,同样设定一定期望脉冲为正弦信号,周期为2.5 s,观察幅值为(折算到摆臂的角度)40.77°,45.30°,56.63°,67.95°的正弦信号跟踪性能.通过实验发现,在给定幅值(30 000脉冲,约67.95°)的情况下,位置控制的轨迹跟踪和正弦信号的周期/频率有关,信号周期大于等于5 s时,位置控制实现较理想,当频率增大时,响应逐渐变差;类似地,在给定相同周期(均为2.5 s)的情况下,位置控制的轨迹跟踪情况和正弦信号的幅值有关,信号幅值小于等于20 000脉冲(折算到摆臂约45.30°)时,位置控制实现较理想,当幅值继续增大时,响应逐渐变差.因此,需进一步分析响应变差原因.

经过多次实验,最终发现驱动系统硬件限制、电机转速达到最大是电机跟踪响应变差的主要原因.图5为期望转角为正弦信号、周期均为2.5 s、不同幅值(40.77°,45.30°,56.63°,67.95°)下的响应跟踪曲线.可以看到,随着幅值的增加,响应越来越差.与此同时,可以看到占空比长期处于0值的时间越来越长,说明电机长期处在全电压(实验中为18 V)工作状态,因此,不管PID如何调节,驱动电压始终达到最大值,转速为全速.由此判定,响应变差是由于驱动系统硬件条件约束所致.

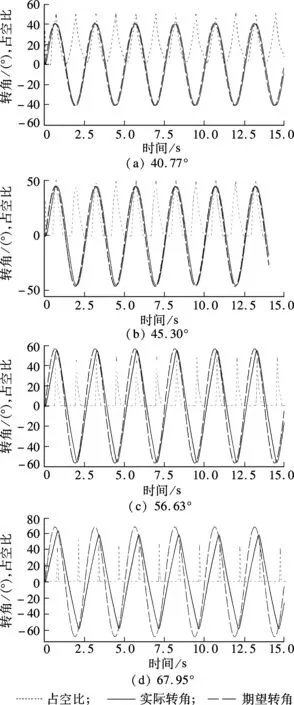
图5 不同摆臂幅度的跟踪响应

4.3 力矩控制实验

首先,设定期望电流为正弦信号,幅值设定为40(数字量),改变正弦信号频率(周期分别为10,5,2.5,1.25 s),观察跟踪响应情况;其次,同样设定期望电流为正弦信号,周期均为2.5 s,改变正弦信号幅值(分别为10,20,30,均为程序中的数字量),观察跟踪响应.由于电流始终为正,因此程序中必须将电流取绝对值.通过实验发现,给定相同幅值而频率不同的正弦电流值时,当周期大于等于5 s,其实际电流跟踪期望电流的性能较理想,可以很好地实现力矩控制,当频率再增大时,跟踪响应变差;但是与位置控制不同的是,给定周期相同而幅值不同的正弦期望电流时,随着幅值的减少,其响应并没有逐渐变好,同时,占空比在多个幅值下均未长期处于0的状态(见图6),也就是说,对于响应的制约硬件系统并不是主要的原因，因而需进一步分析响应变差原因.

图6 不同电流幅值的跟踪响应曲线

经过多种因素的验证与排查,发现响应变差的主要因素为PID参数.对PID参数为Kp=0.2,Ki=0.1,Kd=3和Kp=0.2,Ki=0.325,Kd=3的阶跃响应进行实验.实验中,给定期望电流为相同的阶跃值(均为20),观察不同PID参数下控制系统的阶跃响应特性.根据控制理论,上升时间ts为从起始响应时间开始至进入允许误差范围(一般误差允许范围为小于5%)的时间.由此可得,Kp=0.2,Ki=0.1,Kd=3的阶跃响应上升时间ts约为700 ms,而Kp=0.2,Ki=0.325,Kd=3的阶跃响应上升时间ts约为60 ms,由此可以看出，后者响应明显加快.

在以上结果的基础上,改变PID参数为Kp=0.2,Ki=0.325,Kd=3，重新对周期相同而幅值不同的正弦电流跟踪响应进行实验,得到类似于图6的实验曲线.此时,PID参数调整后其跟踪响应的性能明显提高.

4.4 位置/力矩控制切换实验

4.4.1 基于时间的切换

图7为2种控制模式基于时间(切换时刻为20 s)的切换实验结果.实验时,在位置控制阶段(20 s前),给定的参考位置幅值为15 000脉冲(约34°)、周期为10 s的正弦信号;力矩控制阶段(20 s后),给定的期望电流为幅值45、周期为10 s的余弦信号,由于电流没有负值,因此取其绝对值作为期望值.

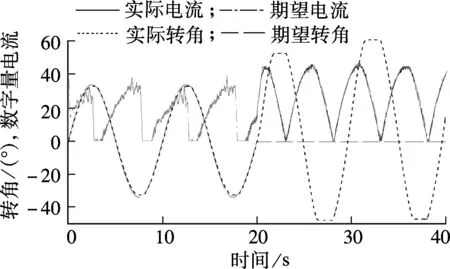
图7 20 s时由位置控制切换为力矩控制

实验时,程序中先设定位置控制,使电机按照预期正弦信号来回摆动,此时可以从图7中看到在PID控制下电机实际转角能够较好地跟随期望转角;当切换时间达到20 s时,位置控制切换为力矩控制,为了防止电流突变,将记录的电机实际电流作为期望电流,然后设定期望电流作为线性函数的起点,线性增加直到余弦信号的幅值为45.此后期望电流设定为幅值为45、周期10 s的余弦信号.由图7中的曲线可看出,20 s切换后,首先电机电流线性增加,直至余弦信号幅值为45,然后数字量电流在PID控制下跟踪期望电流,完成力矩控制.

4.4.2 基于电流的切换

图8为2种控制模式切换前后检测到的电机电流的变化曲线.在程序中,设定电流的阈值为60,若检测到反馈的数字量电流值大于60时,则将位置控制切换为力矩控制.

在位置控制阶段,同样给予一个正弦变化的期望转角,使电机跟随期望脉冲转动;此时电机电流周期性变化;在满足切换条件反馈数字量电流大于设定值60时,则由位置控制切换为力矩控制,此时给定一个期望数字量电流值70,通过PID控制使得电机电枢数字量电流达到70,从而输出恒定力矩,完成力矩控制;当检测到的数字量电流值满足切换条件(反馈数字量电流小于设定值60)时,则由力矩控制切换为位置控制,继续进行位置控制,如此循环.在实验时,为了满足切换条件,通过给摆臂一个人为的瞬间冲击使电机停转,因而使得负载力矩急剧上升.

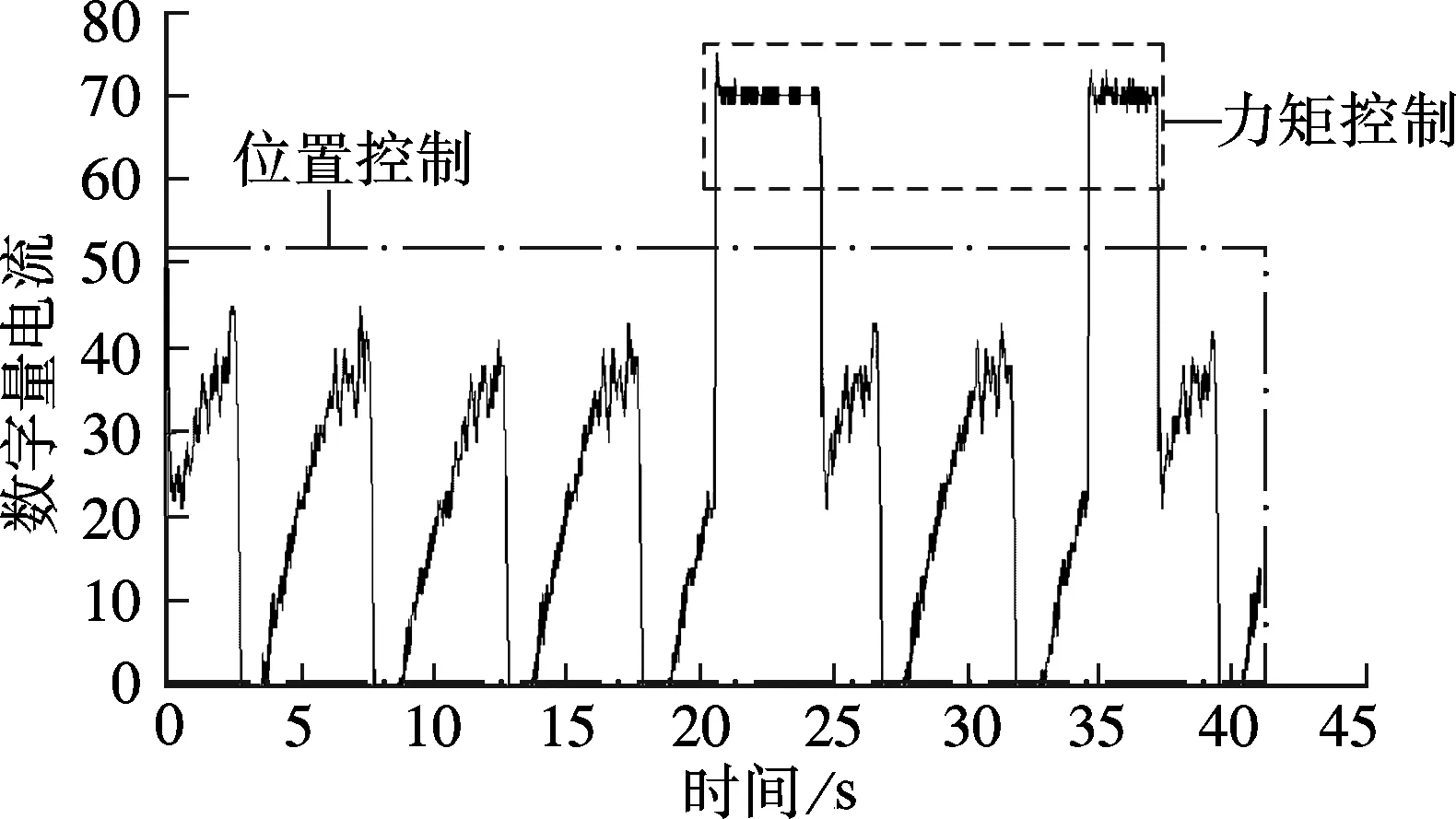
图8 基于电流的切换实验

图8中的中心线框为位置控制时的电枢数字量电流值，设电流值随着位置正弦信号的变化而呈周期性的变化;虚线框为力矩控制时的电枢数字量电流值,该电枢数字量电流值始终与设定的数字量电流值一致,由此可以看出,基于电流的切换是可行的.

5 结论

1) 所设计的控制器能通过设定电流值来改变驱动力矩大小,达到力矩控制的目的;

2) 所设计的控制器能实现位置控制，且影响其响应速度的因素主要是驱动系统硬件;

3) 所设计的控制器能够实现力矩控制，且影响其响应速度的因素主要是PID参数;

4) 所设计的基于电流切换的控制器,能够基于时间和电流平稳地实现位置控制和力矩控制的切换.因此,关节控制器能够应用于机器人关节，从而实现关节的驱动和灵活的控制.

)

[1] 杨敏,殷晨波,董云海,等.拟人步行机器人下肢研究现状 [J].机械传动,2006,30(2):86-88.

Yang Min,Yin Chenbo,Dong Yunhai,et al. Bipedal walking research with humanoid robots [J].JournalofMechanicalTransmission,2006,30(2):86-88.(in Chinese)

[2] Espiau B,Sardain P.The anthropomorphic biped robot BIP2000 [C]//Proceedingsofthe2000IEEEInternationalConferenceonRoboticsandAutomation. San Francisco,CA,USA,2000:3996-4001.

[3] 杨新海.双足步行方法与控制系统研究 [D].哈尔滨:哈尔滨工程大学机电工程学院,2006.

[4] Sakagami Y,Watanabe R,Aoyama C,et al.The intelligent ASIMO: system overview and integration [C]//ProceedingsoftheIEEEInternationalConferenceonIntelligentRobotsandSystems.Lausanne,Switzer land,2002:2478-2483.

[5] Hirai K,Hirose M,Haikawa Y,et al.Development of Honda humanoid robot [C]//ProceedingsoftheIEEEInternationalConferenceonRoboticsandAutomation. Leuven,Belgium,1998:1321-1326.

[6] Kaneko K,Kanehiro F,Kajita S,et al.Humanoid robot HRP-2 [C]//Proceedingsofthe2004IEEEInternationalConferenceonRoboticsandAutomation. New Orleans,LA,USA,2004:1083-1090.

[7] Lee B J,Stonier D,KIim Y D,et al. Modifiable walking pattern generation using real-time ZMP manipulation for humanoid robots [C]//Proceedingsofthe2007IEEE/RSJInternationalConferenceonIntelligentRobotsandSystems. San Diego,CA,USA,2007:4221-4226.

[8] Kumagai M,Emura T.Sensor-based walking of human type biped robot that has 14 degree of freedoms [C]//IEEEProceedingsoftheFourthAnnualConferenceonMechatronicsandMachineVisioninPractice. Toowoomba,Australia,1997:112-117.

[9] 顾星,钟鸣,姚玉峰.基于模糊自适应PID的加样臂位置控制 [J].工程设计学报,2012,19(5):385-390.

Gu Xing,Zhong Ming,Yao Yufeng.Position control for sampling arm based on self-adapting fuzzy-PID[J].ChineseJournalofEngineeringDesign,2012,19(5):385-390.(in Chinese)

[10] 李江道.空间机械臂机电一体化关节的设计与控制 [D].上海:上海交通大学电子信息与电气工程学院,2012.

[11] 孙金凤,姜力.基于关节力矩传感器的灵巧手指的阻抗控制 [J].传感器与微系统,2008,27(7):66-74.

Sun Jinfeng,Jiang Li.Impedance control of dexterous finger based on joint torque sensor [J].TransducerandMicrosystemTechnologies,2008,27(7):66-74.(in Chinese)

[12] Kong K,Bae J,Tomizuka M.Control of rotary series elastic actuator for ideal force-mode actuation in human-robot interaction applications [J].IEEE/ASMETransactiononMechatronics,2009,14(1):105-118.

[13] 周小波.基于DSP的直流伺服驱动的机器人关节控制系统[D].合肥:安徽大学电气工程与自动化学院， 2010.

[14] 苏州均和伺服科技有限公司.MAXON电机手册—产品目录08/09[R].苏州：苏州均和伺服科技有限公司，2008.