离散时间窗下集卡数量动态优化研究
2013-12-23梁承姬
张 彦,梁承姬
(上海海事大学 物流研究中心,上海201306)
随着中国港口经济的发展,各港口集装箱吞吐量不断上升,然而,如何利用现有设备资源对集装箱进行运输和调度,以满足班轮公司的需求,成为港口管理层面临的挑战。由于桥吊为港口稀缺资源,笔者在对港口集装箱运输车辆进行数量优化的同时,将桥吊资源考虑进去并以时间窗作为其资源约束,在满足各任务时间窗约束的情况下保证现有的集卡设备能够得到最大限度的利用。
集卡起着连接岸边桥吊和堆场龙门吊工作的中转作用,其工作效率的高低直接影响到岸边任务完成的时间和堆存任务能否顺畅进行,进而影响到班轮公司能否按照预定时间安排离开泊位。集卡数量在很大程度上影响着码头的工作效率,但是两者并非严格的线性关系。在一定范围内增加集卡数量能够提高码头的工作效率,但是当集卡数量达到一定量的时候,由于港口道路情况的限制,继续增加集卡数量反而会降低码头的工作效率。同时集卡作业具有动态性,一台集卡可以连续工作,完成多个任务,因此有关集卡数量的动态优化也成为可能。集卡的数量问题是关系到整个港口生产效率和成本的关键问题。
目前国内外有关集卡配置的研究比较少,大部分是附带在集卡调度问题上,但是一次的集卡调度得出的集卡数量可信度并不能令人信服,因此对于集卡配置问题还需要进行单独研究。PYUNG 等采用两阶段启发式研究了港口静态环境下集卡数量和路径问题。第一阶段以车辆运输时间最短为目标,求得AGV 的数量下限[1]。第二阶段采用禁忌搜索算法在AGV 数量最少情况下求解AGV 路径问题。MAURO 等采用启发式对有时间窗约束的集卡数量和路径问题进行了研究,并给出了比较详细的启发式算法步骤[2]。IRIS 等研究了时间窗约束下,运输车辆数量最小化问题[3]。PYUNG 等研究了有多个收发点的AGV 数量问题,使用排队模型来估计部分等待时间,在满足预定的等待时间约束情况下,按照最近车辆优先选择的原则,对AGV数量最小化进行了求解,并进行了多次实验来进行验证[4]。JI 等对自动化码头的运输系统进行了数学分析,提出了一个近似的数学分析模型,并进行了多次仿真实验对模型进行了验证[5]。NGUYEN和KIM 建立了混合整数规划模型求解自动化码头中跨运机的最优任务问题,并针对问题的时间复杂度建立了启发式算法以满足计算时间要求[6]。KIM 和BAE 针对已知的集装箱作业任务顺序表安排如何调度AGV 小车,使用了混合整数规划对小车的作业任务安排进行了优化,最后采用启发式算法对模型进行了求解[7]。
国内对集卡数量问题的研究比较少,往往是数量问题包含在路径优化模型中。王军和许晓雷研究了作业面模式下,综合考虑岸桥作业时间、场桥作业时间,建立了以装卸箱总作业时间最短为目标的集卡路径问题。其思路是将所有集卡简化成一台集卡进行作业,因此并没有考虑集卡数量问题[8]。曾庆成和杨忠振研究了集装箱港口装卸过程中集卡调度问题和最小化装卸桥等待时间[9]。赵宁等研究了集卡的利用率,建立了集装箱港口发箱任务的集卡指派模型[10]。杨静蕾、丁以中以上海外高桥集装箱码头为例,构建包括多种设备资源的动态多级排队网络,通过仿真得出了最优机械配比和岸桥台数[11]。韩晓龙研究了装卸作业中的资源配置问题,在岸桥分配优化的动态规划模型之后,提出集卡的配置模型,求出保证岸桥连续作业的集卡最小配置数量并对集卡路径问题进行了研究[12]。
从以上研究可以发现,针对集卡数量问题进行的单独研究还很少,把运输车辆数量和路径综合进行研究往往只关注如何安排集卡路径而忽视了对集卡数量进行优化,由于单独研究车辆数量问题对实际减少港口运作成本影响很大,因此将集卡数量作为关键问题进行深入研究很有必要。
1 问题描述
岸桥装卸的每个任务都有一个时间窗,[sti,dti]表示最早开始时间和最晚结束时间。时间窗是在比较滞后成本和提前成本的基础上均衡得到的,同时由于时间窗的存在,使桥吊和集卡工作具有更多的灵活性。码头前沿加一个缓存区,能够更合理地使用桥吊,减少桥吊的工作等待时间,同时有利于集卡的调度。时间窗的分段数就是缓存区的大小。为了使集卡数量最小,集卡可以在满足前后两个任务时间约束的前提下自由地选择开始时间,可大大地方便集卡的调度工作。集卡的前后任务可以用一个最大流网络图来表示,如图1 所示。网络图节点代表任务的时间窗,由于每个任务只能由一辆车来运输,因此弧的最大流量为1,据此寻找完成所有任务所需的最少集卡数量。

图1 网络示意图
2 集卡数量计算模型
2.1 前提和假设
集卡数量计算模型假设如下:①集装箱任务总数已知;②每个集装箱的最早开始时间和最迟结束时间已知;③每个集装箱的起点和目的地均已知;④有足够的场桥处理集卡所运集装箱,不考虑场桥因素;⑤集卡开始工作位置和结束位置都位于同一位置;⑥不考虑集卡拥挤的干扰。
该模型是在已知集装箱预编排计划下建立的集卡需求量模型,故有关集装箱的数量和堆存位置都是已知的,因此假设①到假设③都是合理的。由于桥吊是稀缺资源,集装箱港口一般会优先考虑桥吊作业,而场桥数量一般都能满足要求,即不允许场桥耽误集卡运输时间,因此假设④也是合理的。在港口集卡开始工作前和结束工作后都有固定的位置用来停放集卡,因此假设⑤是合理的。该模型建立过程中并不考虑集卡数量过多造成的干扰,可以不考虑拥挤的因素。
2.2 模型建立

建立的混合整数规划模型如下:

上述公式的含义为:
式(1)为在起始节点,流出减流入为v,即所使用的最少数量;
式(2)为在终止节点,流出减流入为-v;
式(3)为在中间节点,流入=流出;
式(4)为每个集装箱只能运输一次,因此只有一个开始时间;
式(5)为两个集装箱由同一辆集卡相继完成所需满足的条件;
式(6)为所有集装箱任务的工作时间加上相继任务的准备时间之和要小于总的工作时间;
式(7)和式(8)表示决策变量为0/ 1 变量。
3 数值仿真示例分析
仿真采用随机生成的数据,使用Cplex V12.2求解器对上述模型进行模拟。用于测试的计算机配置为:Intel(R)Core(TM)2 Duo CPU T5450 @1.66 GHz,0.99 GB RAMS。
3.1 测试问题和参数设置
数值仿真进行了3 组实验,每组实验的时间数据都采用随机生成得到。设总工作时间为T。其中,每个任务的工作时间wi通过均匀分布U(1,3)产生,每个任务的开始时间si通过均匀分布U(0,T)生成,而任务i 和任务j 的准备时间Pij通过均匀分布U(0,3)生成。
第1 组实验是对集卡的使用数量进行频数统计,实验数据如表1 所示,工作时间从100 min 逐步增加到200 min、300 min 和400 min,从而计算不同集卡数量出现的次数。为了保证实验的随机性,该实验在不同的工作时间下对20、30、40、50个任务各进行10 次实验,每个工作时间作为1 组实验进行汇总,最后汇总4 组实验结果,也就是在每个工作时间下总共进行了40 次实验,而总实验次数是160 次。第2 组实验是对集卡的数量增长率进行分析,所采用的实验数据与第1 组实验一致,在集卡数量分别为2 台和3 台的情况下,观测集卡数量随任务量变化的情况,同时对比在4 种工作时间情况下,两种集卡数量出现频数的变化趋势。第3 组实验是对集卡的使用数量与工作量之间的关系进行分析,实验组合如表2 所示,在工作总时间为100 min,对任务由20 个最终增至200 个的不同实验组情况下,每组进行10 次随机实验,观察集卡使用量的变化情况。

表1 第1 和第2 组实验组合
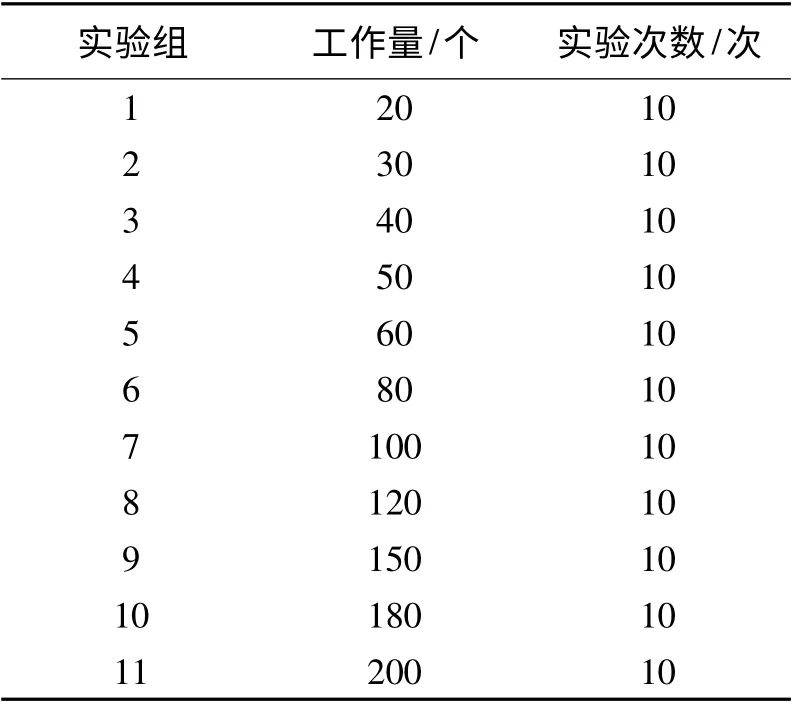
表2 第3 组实验组合
3.2 结果分析
要注意的是,模型的重点并不在于求解集卡路径,由于每次实验的结果都是变动的,因此由所得结果无法判定哪次实验所得路径是集卡最优路径。在确定了集卡的最优数量之后,可以根据实验结果与集卡最优数量相吻合而得到的集卡路径,参考安排集装箱的位置。
(1)第1 组实验结果分析。由表1 数据,使用Cplex V12.2 求解,可得到表3 数据。

表3 集卡使用频数统计
由表3 可看出,随着时间的变化,在相同任务量下,工作时间越长,集卡平均使用量越低,由此可以看出,在总任务量较少的情况下,使用2 台集卡基本可满足要求。在相同任务量下,集卡工作时间越长,其可闲置的时间就越多,因此可以使用较少数量的集卡来完成所有任务。在总工作时间为300 min 时,2 台集卡出现的次数是最多的,这时可以仅安排2 台集卡工作,即能满足要求。
(2)第2 组实验结果分析。集卡数量增长趋势如图2 所示。由图2 可看出,总工作时间越短,集卡数量增加的速度越快。当任务由30 个增到40 个,总工作时间为400 min 的情况下,10 次实验中3 台集卡出现的次数由2 次增加到4 次,频数增加了20%;而当总工作时间减小为100 min时,在10 次实验中,3 台集卡出现的次数立即由2次增加到了7 次,频数增加了50%。也就是说,在集卡调度过程中,总工作时间与成本成反比,减少集卡的使用成本,是以增加工作时间来保证的。

图2 集卡数量增长率趋势图
(3)第3 组实验结果分析。图3 为集卡数量变化趋势图。可以看出,随着工作任务的增多,集卡的使用数量有逐渐增加的趋势。当工作时间固定为100 min 时,随着任务量的增加,3 台集卡出现的次数逐渐增加,而2 台集卡出现的次数相应减少。在任务量为40 个时,2 台集卡出现的次数骤减,从8 台降低到3 台,说明任务量超过40 个时,2 台集卡已经远远无法满足工作需求。在任务量为120 个时,2 台集卡已经不能满足要求,10次随机实验集卡使用量均为3 台。继续增加任务量,集卡使用量增加到了4 台,随着任务量的继续增加,3 台集卡出现的次数在降低,而4 台集卡出现次数逐渐增加,但在120 ~200 个任务范围内,3台集卡的出现频数保持在90%。据此可将工作时间为100 min,任务量为40 个看作转折点。当任务量小于40 个时,选择2 台集卡,当任务量在40 ~200 个之间时,选择3 台集卡。这样安排集卡既能满足任务量需求,又能保证集卡使用成本最低。

图3 集卡数量随工作量变化趋势图
4 结论
针对集装箱港口运输过程,为保证桥吊资源得到优先满足,为集装箱任务添加了时间窗约束,从而为工作过程中需要的集卡数量问题建立了一个MIP 模型,目标是按既定的集装箱任务编排表确定最少的集卡使用量。笔者采用随机模拟工作时间,采用连续递增的时间窗,将任务的最晚结束时间限制在一定的范围内,从而在满足相继任务时间窗的条件下对问题进行了求解。数值仿真成功地对模型进行了求解,得到了合理的集卡数量,同时通过对比分析,也说明了任务量和集卡数量的相关关系。仿真结果从理论上保证了模型的现实意义,比较符合现实的生产状况。
[1] PYUNG H K,WOON S L,DONG W J.Fleet sizing and vehicle routing for container transportation in a static environment[J].OR Spectrum,2004(26):193-209.
[2] MAURO D A,MICHELE M,CORRADA P,et al.Heuristic approaches for the fleet size and mix vehicle routing problem with time windows [J]. Transportation Science,2007,41(4):516-526.
[3] IRIS F A,VIS R B M,DE K,et al.Minimum vehicle fleet size under time-window constraints at a container terminal[J]. Transportation Science,2005,39(2):249-260.
[4] PYUNG H K,JAEJIN J,JUNGDAE S. Estimation of part waiting time and fleet sizing in AGV systems[J].The International Journal of Flexible Manufacturing Systems,2005(16):211-228.
[5] JI M,XIA J.Analysis of vehicle requirements in a general automated guided vehicle system based transportation system[J].Computers & Industrial Engineering,2010(59):544-551.
[6] NGUYEN V D,KIM K H. A dispatching method for automated lifting vehicles in automated port container terminals[J]. Computers & Industrial Engineering,2009(56):1002-1020.
[7] KIM K H,BAE J W.A look-ahead dispatching method for automated guided vehicles in automated port container terminals[J].Transportation Science,2004,38(2):224-234.
[8] 王军,许晓雷. 集装箱码头集卡作业的路径选择[J].大连海事大学学报,2011,37(2):25-27.
[9] 曾庆成,杨忠振.集装箱码头集卡调度模型与Q 学习算法[J].哈尔滨工程大学学报,2008,29(1):1-4.
[10]赵宁,宓为建,何军良.集装箱码头发箱任务的集卡指派模型[J].上海海事大学学报,2011,32(1):8-12.
[11] 杨静蕾,丁以中.集装箱港口设备配置的模拟研究[J].系统仿真学报,2003,15(8):12-17.
[12]韩晓龙.集装箱港口装卸作业资源配置研究[D].上海:上海海事大学图书馆,2005.
