网络计划多资源均衡优化遗传算法

欧阳红祥，刘炳胜，李 欣

(河海大学 商学院，江苏 南京210098)

对资源进行优化配置是保证资源合理使用的重要手段。资源优化有两类问题，一是资源有限工期最短问题，二是工期固定资源均衡问题。工期固定资源均衡问题理论上属于组合优化问题，目前解决该类问题常用的方法是启发式算法，许多学者根据具体问题提出了多种算法。由于启发式算法的优化准则、算法都与特定的问题有关，因此算法的可移植性和通用性比较差。遗传算法是一类可用于复杂系统优化计算的鲁棒搜索算法，与其他方法相比，具有自行概率搜索、运算并行性，以及搜索效率高等优点。文献［1－8］对遗传算法在多资源均衡优化中的应用作了一些探索，但对交叉算子及变异算子对约束条件的破坏问题没有涉及或没能提出较好的方法。基于此，笔者提出了一种简易可行的方法，对基本遗传算法作出了较大改进。

1 多资源均衡优化模型

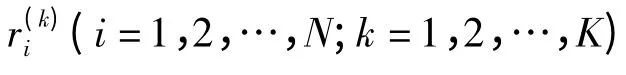
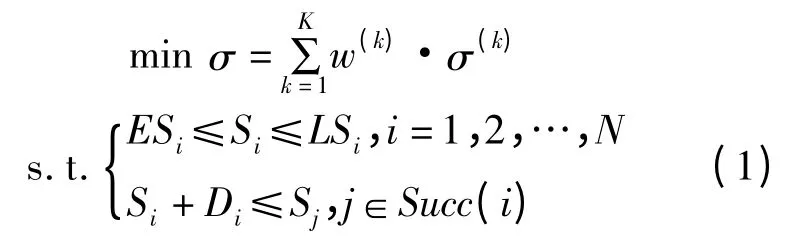
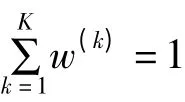
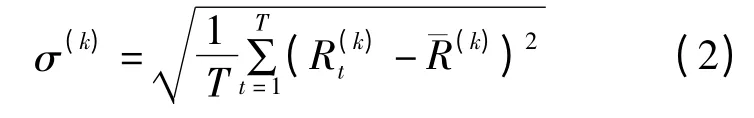
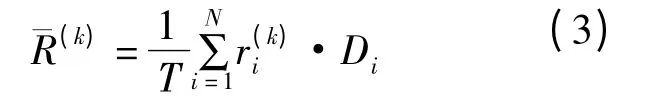
2 遗传算法

2.1 遗传算法流程

遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法，它最早由美国密执安大学的HOLLAND 教授提出。20 世纪70 年代JONG 基于遗传算法的思想，在计算机上进行了大量的纯数值函数优化计算实验。在一系列研究工作的基础上，20 世纪80 年代由GOLDBERG 进行归纳总结，形成了遗传算法的基本框架［9－10］，如图1 所示。

图1 遗传算法流程图

2.2 染色体编码

迄今为止，人们针对实际应用问题提出了许多种不同的编码方法，总的说来，这些编码方法可以分为3 大类:二进制编码、浮点数编码和符号编码。

2.3 适应度函数

在遗传算法中，以个体适应度的大小来确定该个体被遗传到下一代群体中的概率。个体的适应度越大，其被遗传到下一代的概率也越大;反之，个体的适应度越小，其被遗传到下一代的概率也越小。在遗传算法中，通常采用目标函数直接作为适应度函数。

2.4 选择运算

选择运算的作用是从当代群体中，选择出一些比较优良的个体，将其复制到新一代群体中。常用的选择运算包括:①轮盘赌选择法;②随机遍历抽样法;③局部选择法;④竞标赛选择法。

2.5 交叉运算

交叉运算指两个相互配对的染色体按某种方式交换其部分基因，从而形成两个新的个体。依据个体编码方法的不同，有两类算法:①实值重组，包括离散重组、中间重组和线性重组等;②二进制交叉，包括单点交叉、多点交叉和均匀交叉等。

2.6 变异运算

变异运算指对群体中的每一个个体，以某一概率改变某些基因座上的基因值。依据个体编码方法的不同，有两类算子:①实值变异;②二进制变异。

2.7 群体大小

群体大小即群体所含个体数量，取20 ～100为宜。

3 资源均衡优化遗传算法及算例

某网络计划如图2 所示，箭线上方数字为活动所需资源数量(假设项目中所有活动使用3 种资源)，箭线下方数字为活动持续时间(单位为天)，假定3 种资源的权重分别为0.2，0.4，0.4。

图2 活动所需资源数量

3.1 计算活动的时间参数

根据给定的网络计划，采用关键线路法(critical path method，CPM)计算各项活动的最早开始时间(ES)和最迟开始时间(LS)。活动时间参数计算结果如表1 所示。

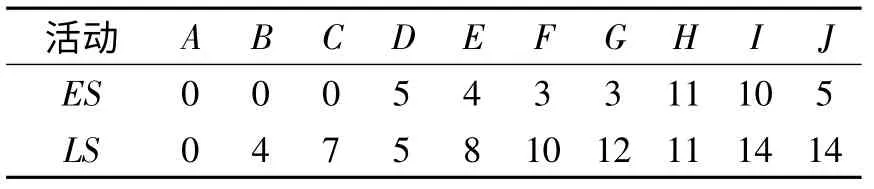
表1 活动时间参数

3.2 浮点数编码

考虑到资源均衡优化目标函数以及约束条件的复杂性，笔者采用浮点数编码方法。以活动的计划开工时间作为决策变量，个体的编码长度等于其决策变量的个数，个体的每个基因值用区间［ES，LS］内的一个浮点数来表示，如图3 所示。

图3 浮点数编码

3.3 产生初始种群

为满足约束条件，可按如下规则产生初始种群:①假如Pred(j)=φ，Pred(j)为活动j 的紧前活动，则在区间［ESj，LSj］内随机生成一个计划开工时间Sj。②若Pred(j)= i，则Sj应在区间［max{ESj，Si+Di}，LSj］内随机取值。③依此类推，随机产生20 个个体形成初始种群，初始种群中的所有个体都满足两个约束条件。

3.4 适应度函数

遗传算法中以个体适应度的大小来评定各个个体的优劣程度，从而决定其遗传机率的大小。该例中，目标函数σ 总取非负值，并且是以求函数值最小为优化目标，因此适应度函数直接取为σ。

3.5 选择运算

笔者采用轮盘赌选择法来选择遗传个体，其基本思想是:各个个体被选中的概率与其适应度大小成正比。具体过程为:①先计算出群体中所有个体的适应度总和;②计算每个个体的相对适应度大小，即为该个体被遗传到下一代的概率;③使用模拟赌盘操作(即0 到1 的随机数)来确定各个个体被选中的次数。

3.6 交叉运算

笔者采用单点交叉算子。采用交叉算子生成的新个体，其对应活动的计划开工时间有时会违背第2 个约束条件，因此，需对单点交叉算子进行改进。改进的思路为:从左至右逐一检查交叉点后的基因值，若对应的计划开工时间违反活动间的逻辑关系，则在区间［max(紧前活动计划完工时间)，该活动最迟开工时间］内随机抽样取值对其进行修正，其过程如图4 所示。

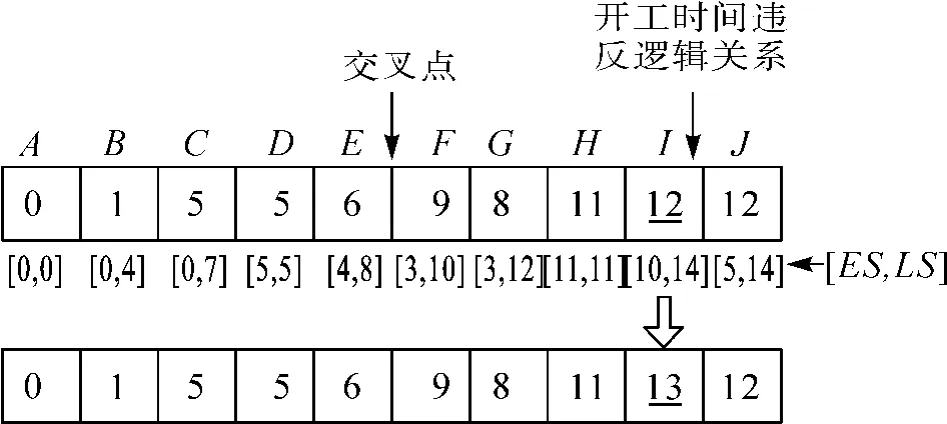
图4 交叉算子改进示意图

3.7 变异运算

笔者采用均匀变异算子。同样，采用变异算子生成的新个体，其对应活动的计划开工时间有时会违背第2 个约束条件，因此，也需对变异算子进行改进。改进的思路为:若变异点的基因值违反活动间的逻辑关系，则在区间［max(紧前活动计划完工时间)，min(紧后活动计划开工时间－该活动持续时间)］内随机抽样取值代替原来的值，其过程如图5 所示。

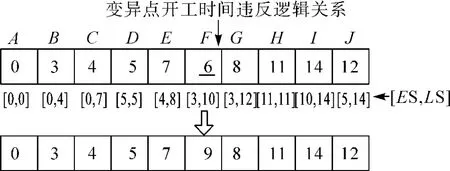
图5 变异算子改进示意图

3.8 运算结果

利用Matlab 7.0 提供的遗传算法工具箱，并结合具体问题编制相应的适应度函数、选择函数、交叉函数和变异函数，优化运行过程经过51 代，其适应度函数值下降到4.571。优化后各项活动的计划开工时间如表2 所示。

表2 各项活动计划开工时间

4 结论

遗传算法是一类具有较好鲁棒性的搜索算法，但其交叉算子和变异算子会破坏资源均衡优化模型中的约束条件，容易产生无效解，大大降低了遗传算法的效率，笔者研究提出一种新的方法有效地解决了上述问题。案例表明，改进后的遗传算法优化效果明显。

［1］ 刘伟军，袁剑波. 基于遗传算法的工程项目资源优化［J］.计算机工程与应用，2006(21):180－182.

［2］ 谢洁锐，黄忠民，俞守华，等. 一种“工期固定，资源均衡”的神经网络模型设计［J］. 计算机应用与软件，2005，22(1):66－68.

［3］ 骆刚，刘尔烈，王健.遗传算法在网络计划资源优化中的应用［J］.天津大学学报，2004 (2):179－183.

［4］ LEU S S，YANG C H，HUANG J C.Resource level in gin construction by genetic algorithm－based optimization and its decision support system application［J］.Automation in Construction，2000 (10):27－41.

［5］ TAREK H.Optimization of resource allocation and leveling using genetic algorithms［J］.Journal of Construction Engineering and Management，1999(3):167－175.

［6］ 张淑山，张连营. 建设项目多资源优化的进化算法实现［J］.科技进步与对策，2009(11):88－90.

［7］ 张连营，张金平，王亮.工程项目资源均衡的遗传算法及其Matlab 实现［J］. 管理工程学报，2004(1):52－55.

［8］ 王首绪，周学林.遗传算法优化施工网络计划的多种资源均衡［J］. 重庆交通学院学报，2001(6):39－45.

［9］ 玄光男，程润伟. 遗传算法与工程设计［M］.北京:科学出版社，2000:78－102.

［10］雷英杰.Matlab 遗传算法工具箱及应用［M］.西安:西安电子科技大学出版社，2005:13－67.