非线性动力学分析方法在嗓音医学中的应用进展*
2013-12-23徐新林综述郭永清张宇庄佩耘蒋家琪审校
徐新林 综述 郭永清 张宇 庄佩耘 蒋家琪 审校
言语交流是人类社会生存的基本功能,生活质量与嗓音功能密切相关。伴随着日趋频繁的社会交往活动,嗓音疾病的患病率也逐年增加,因此,在治疗嗓音疾病时重视嗓音功能的保护有重要意义。目前,临床上对嗓音功能的评估主要包括:声带振动特征评价、发声质量的主客观评估、喉神经肌肉电生理评估、气流动力学评估等方面[1]。其中,因其客观性、方便性及实用性,声带振动特征评价和发声质量的客观评估在临床上应用广泛。正常声带发声时呈双侧对称的周期性振动,而病变声带可因声带的位置、形状、质量、张力、弹力及粘弹性等发生改变,导致声带产生不规则的振动,从而产生很强的非周期性嗓音声学信号。声带的位置、形状、质量、张力、弹力及粘滞性等因素均会对组织产生非线性影响,病变声带振动的过程不可能只按照某一因素的变化产生线性的变化,而是受多因素的影响产生非线性现象。本文对非线性动力学方法在嗓音医学中的应用进展及相关参数进行综述。
1 非线性动力学方法
非线性动力系统可以呈现周期、拟周期和混沌等运动状态,其中混沌运动是非线性分析的主要对象。非线性系统对初始状态具有高度的敏感性,即状态的极小扰动将导致状态差被迅速放大,最终产生完全不同的输出。为了显示简单非线性系统产生的复杂行为,选取Logistic方程:
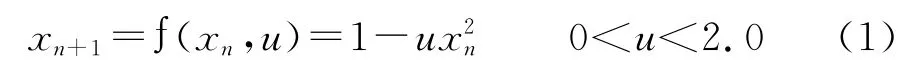
这里f是xn的非线性函数,它依赖于系统参数u和状态变量xn。此方程虽然简单,却明显地显示了从周期到混沌的过程,是研究混沌动力学的典型模型。按如下步骤进行计算机数值模拟实验,首先,在平面上建立一坐标系,x轴为u 值,y轴为xn。在区间(-1,1)内随机取一个数作为x0的初始值,让计算机运行10 000次迭代并舍弃这些数据,然后再开始绘制xn的轨线。通常对每一个u,绘制300点,缓慢增加u值,将得到图1a。从图中可以看到u<0.75时,经过若干次运算xn=xn+1=∧=x∞=A,此时称A 为周期1的吸引子;在u≈0.75和u≈1.25处,可以看到xn的轨线一分为二,二分为四,这时xn的轨迹出现倍周期分支,这种现象称之为倍分叉,因此,方程的输出在几个值间交替的震荡。当参数u超过一定的临界值,系统行为将发生本质的变化,轨迹逐渐变得不轨则,并将产生混沌。在混沌带里,还可以看到周期的轨道。研究表明这种周期分叉到混沌有着深刻的动力学根源,具有相当的普适性[2,3]。
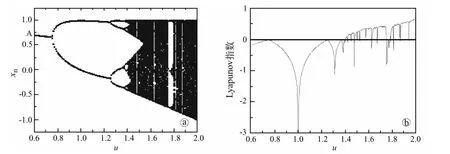
图1 logistic非线性方程 a:倍周期分岔图;b:Lyapunov指数谱
近年来,非线性动力学特别是分形几何和混沌科学的理论被广泛地应用于许多领域,包括经济学、生物学、医学[4,5]和社会学等方面的研究。在生物医学中的应用主要是对生物医学信号的非线性动力学参数的计算,进而通过比较这些参数分析结果以得到可靠的医学信息。常用的非线性动力学参数主要包括:维数、熵及李亚普诺夫(Lyapunov)指数。
1.1 维数 维数是用来描述物体的空间几何形状,如1维、2维等日常所说的整数维及如1.5维、3.5维等分数维的几何空间形状。为了分析信号的分形特征,测量的信号在不同时刻之值生成重构坐标矢量,从而构成相空间(即重构相空间)。分形维数分析了信号在不同尺度下相同程度的复杂特性,信号最基本的分形特征就是它的分数维数。关联维是分数维的一种,常被用来分析生物医学信号,按照GP法(Grassberger and Procaccia,1983)计算出来的,它是一个相空间中轨迹的几何度量,描述轨迹中两点的关联性。关联维数值的大小表示相空间中轨迹的复杂或不规则程度,所以能够定量描述嗓音信号的复杂程度。例如,恒定信号(吸引子是一个不动点)的维数是0,周期信号(如正弦波)的维数是1,随信号的复杂程度而逐渐增加,这样就可以定量测量声带振动的信号,评估其复杂性。
1.2 熵 熵是描述信号系统的可预测性,是系统混乱无序程度的量度。在非线性动力学中,用熵来估算产生新信息的速率,如熵趋近于0,则系统在作规则运动(如周期运动),相反,如熵值趋近于无穷,则系统处于完全随机的过程。对于一个混沌系统,可以用熵来测量信号的复杂程度,借此可根据信息的丢失和产生的速率对系统进行分类,判断系统的复杂程度。周期运动的熵为0,随机运动的熵为无限大,混沌运动的熵是一个有限的值,可表示信号的不规则程度,这样也可以量化声带振动的信号,评估其复杂程度。
1.3 李亚普诺夫指数(图1b) 李亚普诺夫指数描述了混沌系统对初值的敏感程度。该指数可以衡量系统相空间相邻轨道的平均指数型发散或收敛的速率,为对系统初值敏感性的一个动态度量。李亚普诺夫指数可以是负值、正值或0,对于n维相空间就有n个李亚普诺夫指数,构成李亚普诺夫指数谱,它们分别表示轨道在相空间不同方向的发散性(表示发散快慢的度量)。对于稳定不变的定态或周期过程这类规则运动,所有李亚普诺夫指数都是负值或0,混沌状态常有个正值李亚普诺夫指数,即如果信号的最大李亚普诺夫指数小于或等于0,便是周期或稳态,如果信号的李亚普诺夫指数大于0,则是混沌运动。如系统为确定性,正的李亚普诺夫指数为确定混沌运动重要依据之一,这样可以判断某种声带振动的信号是否为混沌运动。
混沌系统具有非整数的分数维数、正有限值的熵以及至少一个以上的正李亚普诺夫指数,并且熵的数值以及最大李亚普诺夫指数越大,系统的混沌性越强,系统的动力学程度越复杂。维数则确定了需要系统的自由度数,维数越高,系统需要的自由度数即状态变量越高。故可以通过计算这些参数值的大小来量化信号的复杂程度,从而量化疾病的轻重程度,为临床疾病的诊断、预后评估提供参考。
2 非线性动力学方法在嗓音医学中的研究现状
声带的振动和发声是一个复杂的非线性过程,主要表现在空气动力能转换为声能的过程。声带的非线性本质使得非线性动力学方法在揭示病态嗓音的发声机制上有重要的研究意义;非线性动力学方法可用于声带振动的有限元模型以及声带振动的高速摄影,能够在一定程度上定量测量声带黏膜波;临床嗓音声学信号的分析能够提供非侵入的客观方法评价病态嗓音及其治疗效果,非线性动力学方法为分析病态嗓音声学信号提供了一种新的分析方法,且更能反映产生病态嗓音声学信号的病理生理[5~9]。
2.1 非线性动力学方法在声带振动特征研究中的应用 在病态嗓音的发声机制中,线性理论(扰动方法)很难解释为什么小的声带质量和劲度的改变以及声带的不对称能够使发声质量产生定性的改变(从规则到不规则),这是因为发声是一个复杂的非线性生物力学和空气动力能转换为声能的过程。声带的非线性特性表现在组织应力和应变的非线性关系、声带振动的非线性及声门气压和气流的非线性关系。首先,声带组织是有粘弹性的,其形变并不完全满足弹性体的线性胡克定律,在大的组织形变下,应力和应变明显的表现为非线性时变关系。拉长组织产生的劲度不稳定,而是随着时间而逐渐松驰,这样的粘弹性也表现在两侧声带的碰撞中。其次,声门内的气压和气流满足非线性纳维-斯托克司(Navier-Stokes)方程,在声门下压的作用下,空气以高速冲出于声门处,产生不稳定的声门气流或湍流,声带黏膜形成波动,声带组织性质发生变化时,黏膜的波动情况将发生改变。
临床上,帕金森病、声带疤痕可能导致声带组织硬度异常高,声带麻痹可能导致声带劲度不对称;声带息肉、小结、囊肿等可能导致声带质量和劲度的异常。这些声带疾病所导致的生物机械参数的异常改变产生不规则的声带振动和非周期的嗓音。通过对两侧声带施加不对称的质量、硬度和劲度致声带非对称来模拟声带麻痹时的不规则振动[6~8]表明,当声带的生物机械参数(如硬度、质量、劲度等)超出正常范围时,声带的振动变得不规则。Jiang[9,10]研究声带的模型和离体喉时认为声带的振动是不规则的,非线性动力学方法可有效地描述和定量测量声带不规则的振动。非线性动力学方法在研究声带振动的机制上有重要作用,Tao等[11]应用非线性有限元流固耦合模型,考虑到气流、气压的非线性以及声带组织的非线性,模拟气流动力能与声带组织耦合从而引起声带组织产生振动的情况,并分析声带表面的压力分布情况,非线性有限元模型可以设置复杂的边界条件和查看空间的受力信息,很好的应用于分析嗓音滥用、声带小结或其他病变时声带的振动方式。然而,声带组织的生物力学指标(用于设置非线性有限元模型的边界条件),比如弹性、阻尼、有效质量等,直接与声带的生理特性有关。这些指标通常不能非侵入地在人类活体内测量,目前所得到的指标主要来自于离体人喉或狗喉的指标,而这些与人类活体可能存在一些差别。非线性有限元模型主要还是控制声带不同的初始状态去研究声带振动的机制,是建立在声带起始振动时的声门状态,不但可以影响到声带组织是否能够同时相地开始振动,而且决定了声门区由气流动力学向声能转换过程中的能量损失程度,声带振动的起始状态对声带的整个振动具有重要作用。
2.2 非线性动力学方法在声带黏膜波研究中的应用 声带黏膜的运动是指当声门下气流冲击声带,声带黏膜及黏膜下组织相对于相对固定的声带肌发生周期性的位移,沿着声带内侧面由下至上依次交替地做向内(关闭)或向外(打开)运动的过程,这种类似液体波浪的运动,称为声带黏膜波动[1],是一个三维的运动,不是单纯的直线运动,本身就存在着非线性特性。
Jiang等[12]采用最小二乘法定量提取VKG 图像中声带左、右、上、下四个缘的参数,适合近似于周期的信号,但受声门下压和扫描部位的影响,不能定量分析非对称性的振动。Zhang 等[13]应用高速摄影研究病变声带振动,通过分析声门区域信息显示病变声带振动具有非线性特性,声带黏膜的运动幅度、周期和相位差也可应用非线性动力学方法分析。Mergell等[14]应用高速摄影获得黏膜波动的参数信号导入生物力学模型模拟声带麻痹患者声带不规则振动的动力学,认为麻痹的声带振动动力学为低维吸引子的振动,具有混沌的特性。Tao等[11,15]使用同步理论测量发声时声带所受的压力情况,发现同步连续体模型与实际的声带表面有相同的压力分布,在研究非线性有限元模型时,其可用于研究声带黏膜波幅度的测量和分析。Zhang 等[16]利用高速摄影揭示了声带不规则振动的时空混沌的动力学机理。
声带黏膜是由声带上皮层和固有层浅层组成的,当病变引起声带解剖结构发生改变时,声带黏膜波动将发生改变。临床上,绝大部分嗓音疾病是由声带解剖结构改变而引起的,对声带黏膜波幅度、时相和相位差的改变情况进行定性或定量测量,在嗓音疾病的诊断、治疗和评估预后中具有重要作用。非线性动力学方法可用于声带振动的有限元模型以及声带振动的高速摄影,能够在一定程度上定量测量声带黏膜波。
2.3 非线性动力学方法在分析嗓音声学信号中的应用
Titze(1995年)从非线性的角度,把嗓音声学信号定性地分成三类:第1类信号是周期或者似周期的,含有强烈的基本频率(f0);第2类信号含有强烈的周期调制或次谐波(f0的分倍数);第3类信号是非周期的混沌信号和噪声。目前,这三类嗓音声学信号在临床上的分析多是采用传统的扰动分析方法(如短期幅度和频率扰动方法),其具有对基频的依赖性及对非周期信号的不稳定性[17],第二类和第三类嗓音声学信号常常很不规则而难于提取稳定基频,不适合传统的扰动方法分析。嗓音疾病患者的嗓音声学信号多是第二类和第三类信号,特别是疾病较严重的时候,声学信号已属于不规则且无周期性的第三类信号,已不适合应用传统的扰动方法分析,扰动方法并不合适于分析声带疾病中的嘶哑声和气息声[18]。
Zhang等[19]利用非线性动力学方法表明帕金森、声带小结、声带麻痹患者[20]的嗓音声学信号的关联维数显著高于正常嗓音,这表明描述病态嗓音需要更多的自由度或系统变量。Hertrich 等[21]应用分形维分析帕金森患者的嗓音声学信号,Giovanni等[22]应用最大Lyapunov指数区分了正常嗓音和声带麻痹患者的病态嗓音,于萍等[23]也研究出Lya-punov 指数可以很好的进行嗓音声学信号分析。Jiang[24]应用非线性动力学方法分析正常人和声带息肉患者嗓音声学信号,得出嗓音声学信号具有低维的特征,可将其应用于临床病态嗓音的分析和评估嗓音疾病。这些研究表明非线性动力学方法的各种指标对区别正常和病态嗓音是有价值的。另外,在分析声带息肉患者手术前后的嗓音声学信号时,发现非线性动力学方法可以很好的预估声带息肉切除术后的治疗效果[25];Chai等[26]研究发现男性吸烟者嗓音声学信号的D2 比正常人更高,在评估病态嗓音方面比传统的扰动方法有更好的敏感性。
多个研究显示,非线性动力学方法不需要取代但可补充和完善传统的扰动分析方法在嗓音声学信号分析中的应用[27,28]。Jiang等[29]研究发现声带小结与声带息肉两种嗓音疾病之间的关联维D2有明显差异。非线性动力学方法与传统的扰动分析相比,可以区分不同嗓音疾病,需要更短的嗓音声学信号,更容易适用于强噪声环境,允许更低的采样率[29]。这些优点适合于临床工作中患者配合不好、节奏快、录音条件差等条件下的应用。目前,非线性动力学方法各种指标的计算需要较好的电脑配制、需要新的软件,在临床上应用研究较少,但随着对不规则嗓音声学信号机理的研究不断深入,反映更多的病态嗓音声学信号的特性、非线性动力学方法将会更加实用。
3 展望
嗓音医学是一门研究发声的基本原理、探讨发声障碍的病因、发病机制、治疗及预防的科学。非线性动力学方法为嗓音医学的基础研究提供了一个新的方法,在一定程度上能够定量研究和分析嗓音疾病的特征,为疾病的诊断和预后评估提供参考,在声带发声机制及其影响因素的研究方面有很大的应用前景。非线性动力学方法在分析嗓音声学信号中已取得了重要的进展,但在各种嗓音疾病研究中进一步的定量分析,特别是对嗓音疾病的鉴别能力有待于进一步研究;声带组织的生物力学参数需要进一步测量,以供声带组织与气流在非线性有限元流固耦合模型中声带振动机制的研究并验证模型的正确性;另外,非线性动力学软件还有待于进一步开发以适合于快节奏的临床工作。目前对于声带黏膜波的测量多局限于定性测量,由于牵涉到三维空间和黏膜波的叠加,黏膜波的定量测量还有待于进一步研究。把高速摄影的数字信号处理运用到声带振动的有限元模型中,应用非线性动力学方法和声带振动的有限元模型定量分析声带黏膜波幅度成为一种可能。
非线性动力学方法可以分析周期、拟周期和混沌等运动形式的信号,具有适用性广、实用性强等优点。虽然目前的许多工作尚为初步性的,但已获得了一些很有意义的结果。今后随着非线性动力学分析方法和电脑软件技术的开发,以及高速摄影技术的应用和声带有限元模型的建立以获取各种分析参数,将在嗓音疾病的诊断、治疗、预后以及研究发声机制方面发挥重要的应用价值。
1 韩德民,Sataloff RT,主编.嗓音医学[M].北京:人民卫生出版社,2007.63~64.
2 Moon FC.Chaotic and fractal dynamics:an introduction for applied scientists and engineer[J].American Journal of Physics,1993,61:670.
3 Ellner S.Coping with Chaos:analysis of chaotic data and the exploitation of chaotic systems[J].Bulletin of Mathematical Biology,1995,57:945.
4 Poon CS,Merrill CK.Decrease of cardiac chaos in congestive heart failure[J].Nature,1997,389:492.
5 Hornero R,Alonso A,Jimeno N,et al.Nonlinear analysis of time series generated by schizophrenic patients[J].IEEE Eng Med Biol Mag,1999,3:84.
6 Isshiki N,Tanabe M,Ishizaka K,et al.Clinical significance of asymmetrical vocal cord tension[J].Ann Otol,1977,86:58.
7 Steinecke I,Herzel H.Bifurcations in an asymmetric vocalfold model[J].J Acoust Soc Am,1995,97:1 874.
8 Tao C,Zhang Y,Du GH,et al.Estimating model parameters using chaos synchronization[J].Phys Rev E,2004,69:36 204.
9 Jiang JJ,Zhang Y.Modeling of chaotic vibrations in symmetric vocal folds[J].J Acoust Soc Am,2001,110:2 120.
10 Jiang JJ,Zhang Y,Ford CN.Nonlinear dynamics of phonations in excised larynx experiments[J].J Acoust Soc Am,2003,114:2 198.
11 Tao C,Jiang JJ,Zhang Y.Studying the vocal-fold impact using a self-oscillation finite-element model[J].J Acoust Soc Am,2006,119:3 987.
12 Jiang JJ,Zhang Y,Kelly MP,et al.An automatic method to quantify mucosal wave via videokymography[J].Laryngoscope,2008,118:1 504.
13 Zhang Y,Shao J,Krausert CR,et al.High-speed image analysis reveals chaotic vibratory behaviors of pathological vocal folds[J].Chaos,Solitons,Fractals,2011,44:169.
14 Mergell P,Herzel H,Titze IR.Irregular vocal-fold vibration-High-speed observation and modeling[J].J Acoust Soc Am,2000,108:2 996.
15 Tao C,Jiang JJ,Zhang Y.Measurement of stress in vocal folds during phonation using spatiotemporal synchronization[J].Physics Letters A,2007,362:42.
16 Zhang Y,Jiang JJ.Spatiotemporal chaos in excised larynx vibrations[J].Physical Review E,2005,72:3 520.
17 Titze IR,Liang H.Comparison of F0extraction method for high-precision voice perturbation measurements[J].J Speech Hear Res,1993,36:1 120.
18 Bielamowicz S,Kreiman J,Gerratt BR,et al.Comparision of voice analysis systems for perturbation measurement[J].J Speech Hear Res,1996,39:126.
19 Zhang Y,Rahn D,Jiang JJ.Studying vocal Fold vibrations in parkinson's disease with a computer model[J].Chaos,2005,15:033 903.
20 Zhang Y,Jiang JJ,Biazzo L,et al.Perturbation and nonlinear dynamic analysis of voices from patients with unilateral laryngeal paralysis[J].J Voice,2005,19:519.
21 Hertrich I,Lutzenberger W,Spieker S,et al.Fractal dimension of sustained vowel productions in neurological dysphonias:An acoustic and electroglottographic analysis[J].J Acoust Soc Am,1997,102:652.
22 Giovanni A,Ouaknine M,Triglia JM.Determination of largest Lyapunov exponents of vocal signal:application to unilateral laryngeal paralysis[J].J Voice,1998,13:341.
23 于萍,Maurice O,Antoine G.Lyapunov系数在嗓音障碍评估中的意义[J].听力学及言语疾病杂志,2006,14:175.
24 Jiang JJ,Zhang Y.Nonlinear dynamic analysis of speech from pathological subjects[J].Electronics Letters,2002,38:294.
25 Zhang Y,McGilligan C,Zhou L,et al.Nonlinear dynamic analysis of voices before and after surgical excision of vocal polyps[J].J Acoust Soc Am,2004,115:2 270.
26 Chai LY,Sprecher AJ,Jiang JJ.Perturbation and nonlinear dynamic analysis of adult male smokers[J].J Voice,2011,25:342.
27 Zhang Y,Jiang JJ,Wallace SM.Comparison of nonlinear dynamic methods and perturbation methods for voice analysis[J].J Acoust Soc Am,2005,118:2 551.
28 Dajer ME,Pereira JC,Maciel CD.Nonlinear dynamical analysis of normal voices[J].IEEE,2005,71:765.
29 Zhang Y,Jiang JJ.Nonlinear dynamic analysis in signal typing of pathological human voices[J].Electronics Letters,2003,39:1 021.
