基于LSSVM-GPC的流化床锅炉多变量协调控制方法

孙 立潘 蕾沈 炯

(1清华大学热能工程系, 北京 100083)

(2东南大学能源热转换及其过程测控教育部重点实验室, 南京 210096)

流化床燃烧 (FBC) 方式由于其燃料适应性广,污染排放小,负荷调节能力强等特点,在世界范围内获得迅速推广[1]．但是流化床锅炉的控制问题一直是影响其发展的主要难题之一．多数流化床锅炉的燃烧自动控制系统投入率很低,主要原因在于流化床锅炉比煤粉炉耦合关系更加复杂,滞后更大,常规的控制方法很难取得理想的调节效果[2]．

Clarke等[3]提出的广义预测控制(GPC)算法,能够有效解决时滞和多变量问题．但对于流化床锅炉燃烧系统,由于多个输入输出通道的静态增益和纯滞后时间具有很大的差异,广义预测控制律在矩阵逆运算过程中极易出现病态矩阵[4],导致控制系统输出振荡,调节量波动频繁．目前,对于多变量预测控制的解耦研究还相对较少[4-6],而这对于大型热工设备运行的节能与安全非常关键．流化床锅炉的主要控制对象是床温和锅炉负荷[7],相比目前仿真对象普遍采用的传递函数模型[2],FBC锅炉燃烧系统的机理模型能够更好地体现“床层蓄热”和“虚假床温”等热工对象特殊的动态特性[8].

本文基于最小二乘支持向量机,对GPC所需的模型进行离线辨识,提高辨识精度,减少在线计算时间;针对FBC锅炉多变量系统,基于关联分析方法,提出了一种协调预测控制策略,直接应用于机理模型,获得了良好的综合控制品质．

1 流化床燃烧机理模型

Ikonen 等[9]提出了FBC机理模型，其仿真结果与示范电站的现场数据吻合良好．本文首先建立该FBC机理模型,并将其作为控制设计的对象．该模型主要包含以下几种非线性微分方程.

1) 密相区碳平衡

2) 密相区氧平衡

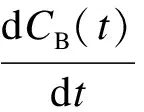
3) 稀相区氧平衡

4) 密相区能量平衡(床温动态特性)

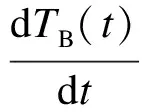
5) 稀相区能量平衡

6) 整体能量平衡(热功率动态特性)

式中,输入量QC为给煤量;F1,F2为一、二次风量; 输出量TB,TF,P,CF,WC,CB分别为床温、稀相区温度、热功率、烟气含氧量、床层含氧量、床料量;V,QB,C1,VB,XC,HC,WI分别为挥发分含量、燃烧率、空气含氧量、床层体积、单位燃料耗氧量、燃料热值和石灰石量;cI,cF，TBt，ABt，αBt，PC分别为石灰石比热、烟气比热、冷却水温、传热面积、传热系数和炉膛燃烧功率;τmix为时间常数．

对本文所建FBC模型进行仿真,在t=1000s时作给煤量和一次风量阶跃,模型的输出响应如图1所示.该模型能体现动态响应初期因床层蓄热引起功率变化和“虚假床温”的现象,正确地反映了FBC锅炉的主要动态特性．

图1 FBC机理模型的阶跃响应

2 流化床燃烧的控制模型

由于FCB机理模型难以直接用于控制算法,考虑到最小二乘支持向量机(LSSVM)在系统辨识方面具有极强的泛化能力[10],因而本文通过采用LSSVM来建立FBC控制模型．

2.1 流化床锅炉的LSSVM辨识建模

以给煤量QC和一次风量F1为输入,床温TB和热功率P为输出,建立流化床燃烧系统双入双出模型,表1给出该系统部分稳态工况点的计算结果．

表1 部分稳态工况点

采用四阶Runge-Kutta法对机理模型进行动态仿真．假设从稳态工况2开始,输入随机激励,使输出在足够大的范围内波动．为比较辨识效果,输出值中加入噪信比为24%的正态白噪声．仿真产生长度步数为300的采样数据,前100步作为训练样本,后200步作为测试集．

基于训练样本,采用LSSVM辨识．通过求解最小化结构风险,得到如下决策函数[10]:

(1)

式中,f表示床温TB或负荷P;x为当前的状态向量;xk为训练样本集;K(x,xk)为核函数;αk和b为训练出的网络参数,辨识结果与实际值的比较如图2所示．

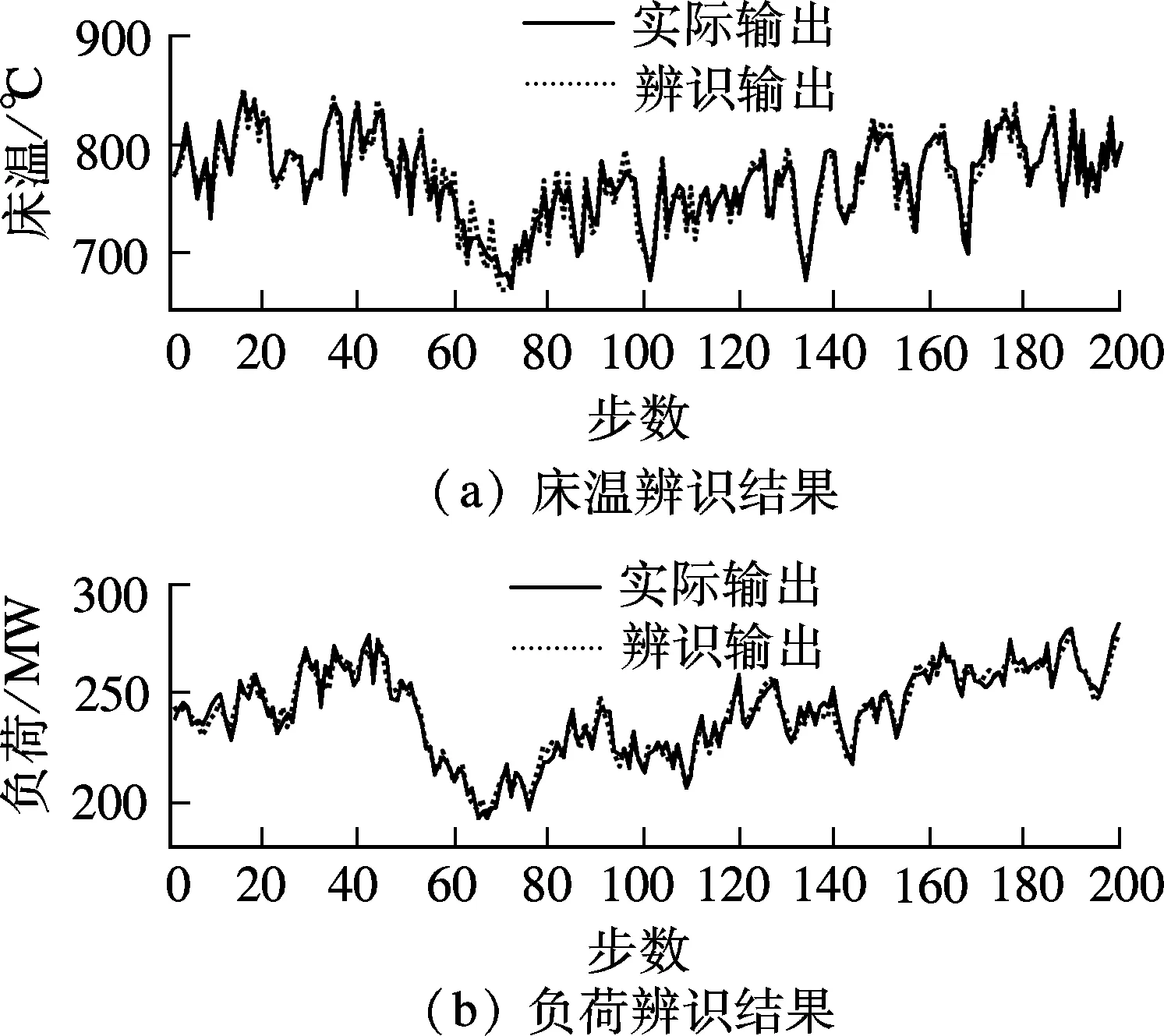
图2 LSSVM的辨识输出与实际输出的比较

2.2 辨识效果的比较及模型选择

分别采用递推最小二乘法(RLS)、子空间法和LSSVM对模型进行辨识.表2给出3种方法辨识结果的均方根误差，均方根误差的计算式为

(2)

表2 3种辨识方法的RMS值

从表2可以看出,LSSVM的辨识效果明显优于RLS和子空间法,特别是长程预测.虽然线性核函数的辨识精度比径向基核函数略低,但径向基核函数所建立的是非线性模型,在线计算开销很大.因此，本文采用基于线性核函数的LSSVM算法辨识,并将决策函数式(1)转化为CARIMA模型[3]，即

(3)

3 FBC锅炉多变量协调预测控制策略

3.1 多变量广义预测控制及其存在的问题

预测控制是解决多变量耦合和大滞后控制问题的先进算法.然而,仅采用预测控制解决FBC锅炉的多变量控制问题,难以得到满意的效果．这是因为预测控制算法未充分考虑控制对象的特性,在现场常会造成2个问题[11]:① 由于控制量之间的耦合关系和计算过程中矩阵可能出现病态,易使本来可以稳定的过渡过程产生震荡乃至发散现象,从而导致控制失效;② 各变量调节频繁,不利于运行节能以及热工设备安全．综上所述,本文通过对FBC锅炉燃烧系统的关联分析,提出改进的FBC协调预测控制策略．

3.2 FBC控制回路的关联分析与稳定性

流化床锅炉控制回路是通过调整给煤量QC(u1) 和一次风量F1(u2)来协调控制床温TB(y1)和热功率P(y2),这是一个2×2的系统.为了设计协调策略,首先需对其进行关联分析．本文采用Bristol提出的相对增益阵列(RGA)的规则[12]，定义控制量uj到被控量yi的相对增益为

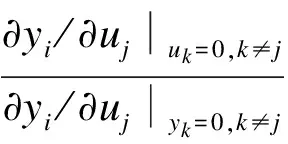
(4)

式中，分子表示除uj外其余回路均开环时uj对yi的增益；分母表示除yi外其余回路都闭环时uj对yi的增益.用这些相对增益可组成2×2的相对增益矩阵Λ．Λ矩阵可用系统稳态增益计算得到.根据FBC机理模型,可获得多个工况的稳态增益矩阵G(0),进而可算出RGA的范围为

(5)

根据RGA的规则可知,λij越接近1,则yi受uj的影响越大．值得注意的是,RGA是稳态分析的结果,下面将结合动态特性以指导设计协调控制的优先权．为分析RGA配对规则的可用性,计算如下NI指标[12]:

(6)

3.3 基于关联分析的FBC锅炉协调控制策略

关联分析和现场经验[7]表明:① 床温调节主要通过一次风量F1(u2)控制,但F1(u2)又必须保证一定的流化速度和欠氧燃烧环境,所以当设定值变化较大时,还需调节给煤量;② 负荷控制中给煤量u1的作用存在大滞后大惯性,而调节一次风的快速性很好,但对稳态负荷几乎不起作用．综上所述,本文提出一种FBC锅炉协调预测控制策略(CBGPC)．以关联分析为基础,通过对被控量加权来监控预测偏差,该控制结构如图3所示．

系统协调决策层是控制系统的中枢,采集实时输出时,根据知识库信息选择控制模式,及时调整控制目标,本文设定知识库中的优先权矩阵为

(7)

式中,Ci为优先权次序，反映了控制目标的2个模式,由工艺工程师确定，本文取C1={y1,αy2},C2={βy1,y2},C1优先于C2,且α,β>1,易见C1对应“床温跟负荷”控制模式,C2则对应“负荷跟床温”控制模式;e1，e2为预测偏差的2个阈值,作为模式选择的依据；控制量u的优先权次序来自于关联分析结果．

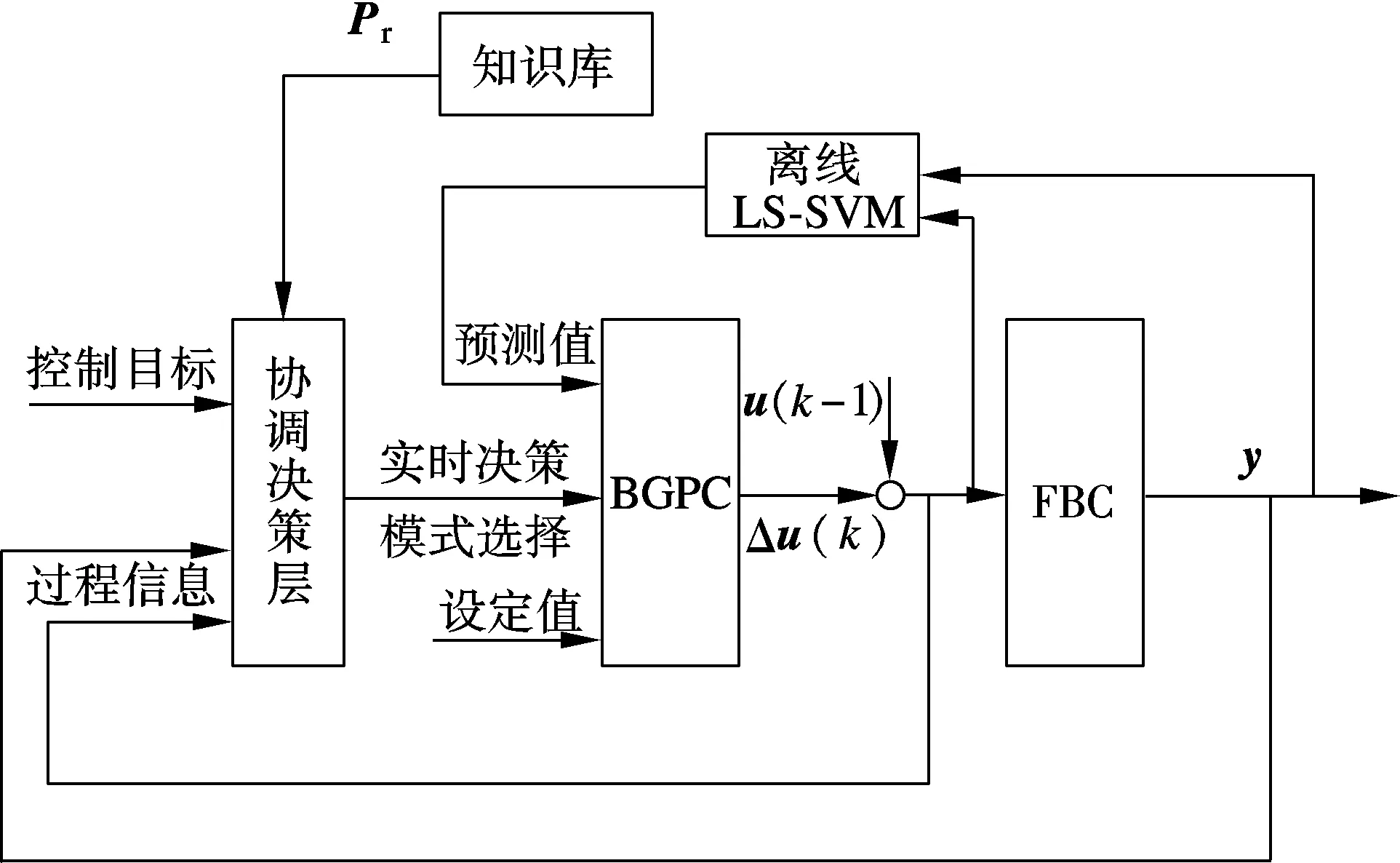
图3 FBC多变量协调预测控制系统结构

具体决策逻辑如下:

IF |C1p-C1r|>e1

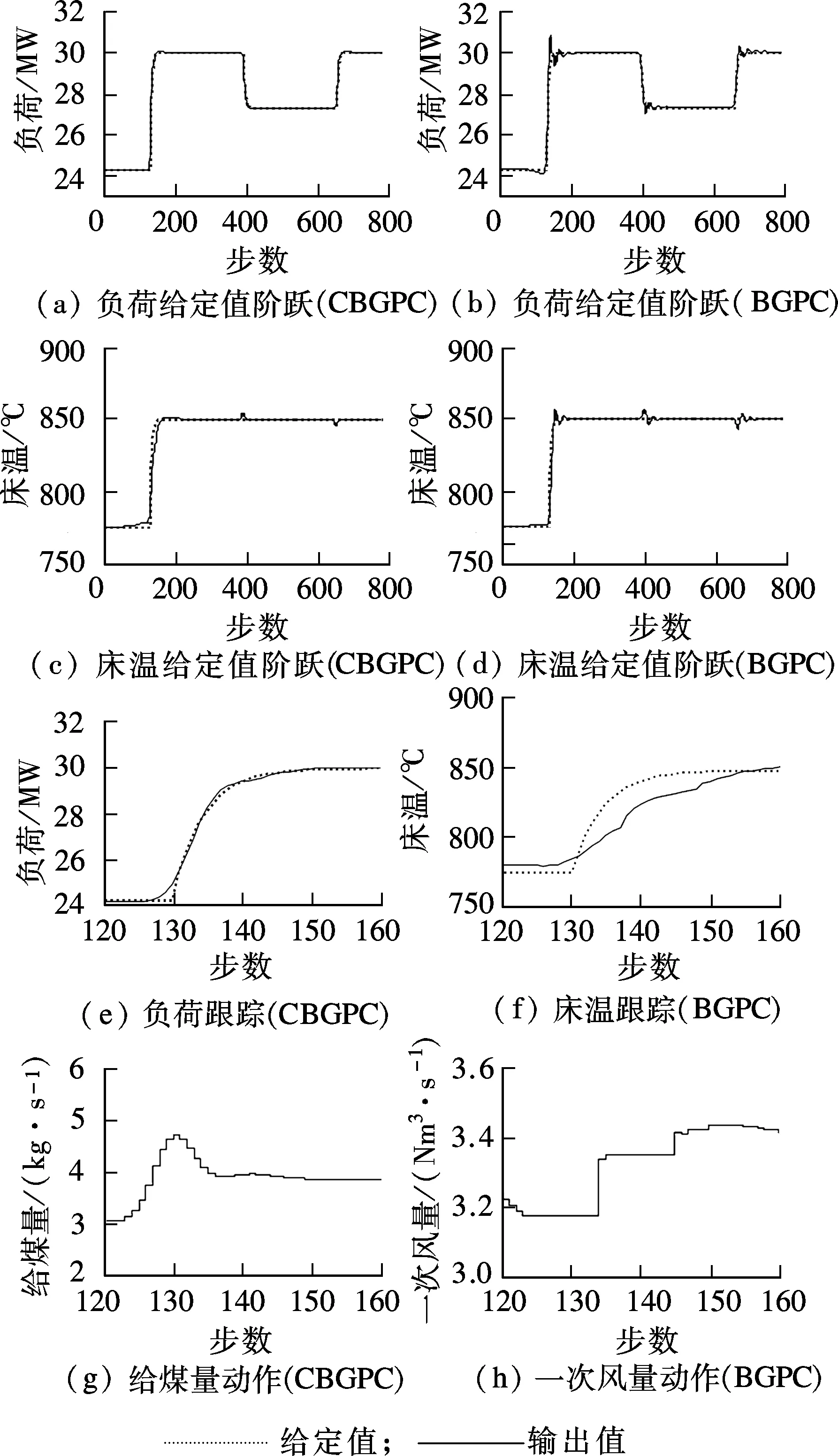
THEN IFu1min

OUTPUT Δu1

ELSE OUTPUT Δu2

ELSE IF |C2p-C2r|>e2

THEN IFu2min

OUTPUT Δu2

ELSE OUTPUT Δu1

ELSE CALL BGPC

END

3.4 仿真实验及分析

根据上述协调控制策略,以给煤量为主控负荷,一次风量为主调床温,且两者相互协调．使用LSSVM辨识出给煤量纯滞后d,所需上一时刻的控制量为

(8)

以FBC微分方程组为仿真对象进行控制仿真,仿真结果与普通BGPC算法对比如图4所示．

从图4可以看出,对于流化床燃烧系统,协调预测控制CBGPC获得了比普通BGPC算法更好的稳定性,能够快速响应负荷指令,且每步只输出一个控制量,避免了调节量的频繁动作．

图4 FBC多变量系统的控制仿真

4 结语

本文首先建立了FBC燃烧系统的机理模型,该模型能够很好地仿真“虚假床温”和“床层蓄热”等独特的动态特性,以此模型为对象,研究了FBC锅炉的辨识和控制．

基于LSSVM离线建立了广义预测控制的CARIMA模型,使得控制规律可以像DMC那样离线计算,大大减少了在线计算量．对测试样本的辨识显示,支持向量机具有明显的精确性,其强大的泛化能力将在系统辨识方面获得更大的应用．

基于关联分析法,提出了一种协调给煤量和一次风量动作的预测控制策略,实现了对床温和负荷的多变量控制．仿真结果显示,该协调控制方法能够实现在负荷快速响应的同时,床温基本维持稳定,为流化床锅炉主控系统的设计奠定了基础．

)

[1]Leimbach R,Automation M. Intelligent control of FBC boilers[J].Power, 2012,156(4):48-51.

[2]牛培峰, 张君.循环流化床锅炉燃烧系统聚类融合控制研究[J].中国电机工程学报, 2007, 27(11): 33-39.

Niu Peifeng, Zhang Jun. Research on clustering fusion control for circulating fluidized bed boilers combustion system[J].ProceedingsoftheCSEE, 2007,27(11):33-39.(in Chinese)

[3]Clarke D W, Mohtadi C, Tuffs P S. Generalized predictive control—part I:the basic algorithm[J].Automatica, 1987,23(2): 137-162.

[4]Kouvaritakis B, Rossiter J A, ChangA O T. Singular-value-decomposition approach to multivariable generalised predictive control[J].IEEEProcControlTheoryAppl, 1993,140(3): 145-154.

[5]Chai T, Mao K, Qin X. Decoupling design of multivariable generalized predictive control[J].IEEEProcControlTheoryAppl,1994,141(3):197-201.

[6]Zhang Ridong, Xue Anke, Wang Shuqing,et al. Partially decoupled approach of extended non-minimal state space predictive functional control for MIMO processes[J].JournalofProcessControl, 2012,22(5):837-851.

[7]党黎军, 赵志丹, 王毕乐. 循环流化床机组控制与保护技术及其应用[M]. 北京:中国电力出版社, 2008: 20-21.

[8]Hadavand A, Jalali A A, Famouri P. An innovative bed temperature-oriented modeling and robust control of a circulating fluidized bed combustor[J].ChemicalEngineeringJournal, 2008,140(1/2/3): 497-508.

[9]Ikonen E, Najim K.Advancedprocessidentificationandcontrol[M]. New York: Marcel Dekker, 2002.

[10]顾燕萍,赵文杰,吴占松.基于最小二乘支持向量机的电站锅炉燃烧优化[J].中国电机工程学报,2010,30(17):91-97.

Gu Yanping, Zhao Wenjie, Wu Zhansong. Combustion optimization for utility boiler based on least square-support vector machine[J].ProceedingsoftheCSEE, 2010,30(17):91-97.(in Chinese)

[11]王树青，金晓明.先进控制技术及应用[M]. 北京:化学工业出版社,2001:99-102.

[12]Niederlinski A. A heuristic approach to the design of linear multivariable interacting subsystems [J].Automatica, 1971,7(6): 691-701.