舰船辐射噪声的响度和音色特征模型

曹红丽 方世良

(东南大学水声信号处理教育部重点实验室, 南京 210096)

水下目标识别是现代海战的重要环节,目标特征的选择和提取是提高目标识别率的关键问题．为了得到有效稳定的识别特征,目前主要利用时域分析、频域分析、时频分析以及混沌分形分析等信号处理方法得到的有效特征进行目标识别．由于目标声学特性的复杂多变性,目标识别率始终无法达到预期要求．实际上,目标识别仍然依赖于声纳员耳听识别结合机器识别来完成目标识别任务．声纳员听音判型方法虽然有效,但是听音判型方法的数学描述很困难．因此,模仿人耳的听声过程是一个非常有前景的研究方向．舰船辐射噪声包括螺旋桨噪声、机械噪声和水动力噪声,其中螺旋桨噪声是主要噪声,声纳员就是根据螺旋桨的噪声进行听音识别[1]．声纳员的听音判型是根据心理声学特征进行识别,心理声学特征包括响度、音调和音色,其中主要依据响度和音色特征．目前,研究者将响度[2-4]和音色特征应用于水下目标识别[5]中,目标识别率得到了一定的提高,但这些方法没有考虑舰船辐射噪声自身的特点,因此建立舰船辐射噪声的心理声学特征模型尤为重要．本文研究舰船辐射噪声的Moore响度模型,从谱质心特征的数学定义推导研究谱质心带宽、谱质心斜度和谱质心峰度的计算公式和物理含义,从而得到舰船辐射噪声的音色特征模型,并将舰船辐射噪声的响度和音色特征模型相结合,应用到实际水下目标识别中．

1 舰船辐射噪声的Moore响度特征模型

响度是描述人耳对声音感觉强度的心理声学量,Moore根据人耳的听觉原理和声波在人耳中的衰减特性,提出更加接近人耳听觉特性的响度计算模型.下面介绍Moore响度[6-8]计算过程．首先对声音信号进行离散傅里叶变换,以1 Hz频率分辨率将声音信号的频率成分进行划分,声音信号就看作是以1 Hz为间隔、幅值不变的正弦声音信号的合成．在信号处理时,采样频率高于声音信号最高分析频率2倍以上,采样点数最好与采样率相同,这样可使信号的能量集中在原有的频率上不出现泄漏．声音信号在传播过程中通过外耳、中耳时,能量会发生变化,这种变化在具体的响度计算模型中用外耳和中耳的传递函数表示,本文采用三次多项式函数进行插值得到传递函数．

首先将经外耳和中耳后的声音信号转换成激励模型,激励级表示的是声音信号经过外耳和中耳后在耳蜗中的声音能量级,根据下式转换为激励级LERB-level:

(1)

式中,ERB带宽Ewidth=24.673(4.368f/1000+1);p0=2×10-5Pa为参考声压;指数权函数w(gk)=(1+pkgk)exp(-pkgk),gk=(fk-f)/f,pk=4f/Ewidth,fk表示有效频率成分的频率值．

声音信号经过耳蜗后到达基底膜,用372个滤波器来模拟基底膜上的响应,即进行特性响度的计算．人耳的听觉频率范围是50～1.5×104Hz,由Enumber=21.366log(4.368Fi/1000+1)换算得到听觉频率范围是1.8～38.9 ERB，其中Enumber为ERB数，Fi为滤波器的中心频率.以0.1 ERB为间隔,得到372个滤波器,声音信号通过372个滤波器后的输出激励Ei为

(2)

式中,i=1,2,…,372;j为声音信号的有效频率数.滤波器采用前面的指数权函数.形式如下所示:

(3)

(4)

根据输出激励计算特性响度,即

(5)

式中,ET为可听阈的能量;G的取值为500Hz以上的ET与500Hz以下的ET的比值;α的取值取决于G的取值;C=0.046871．图1为上述参数值的示意图．

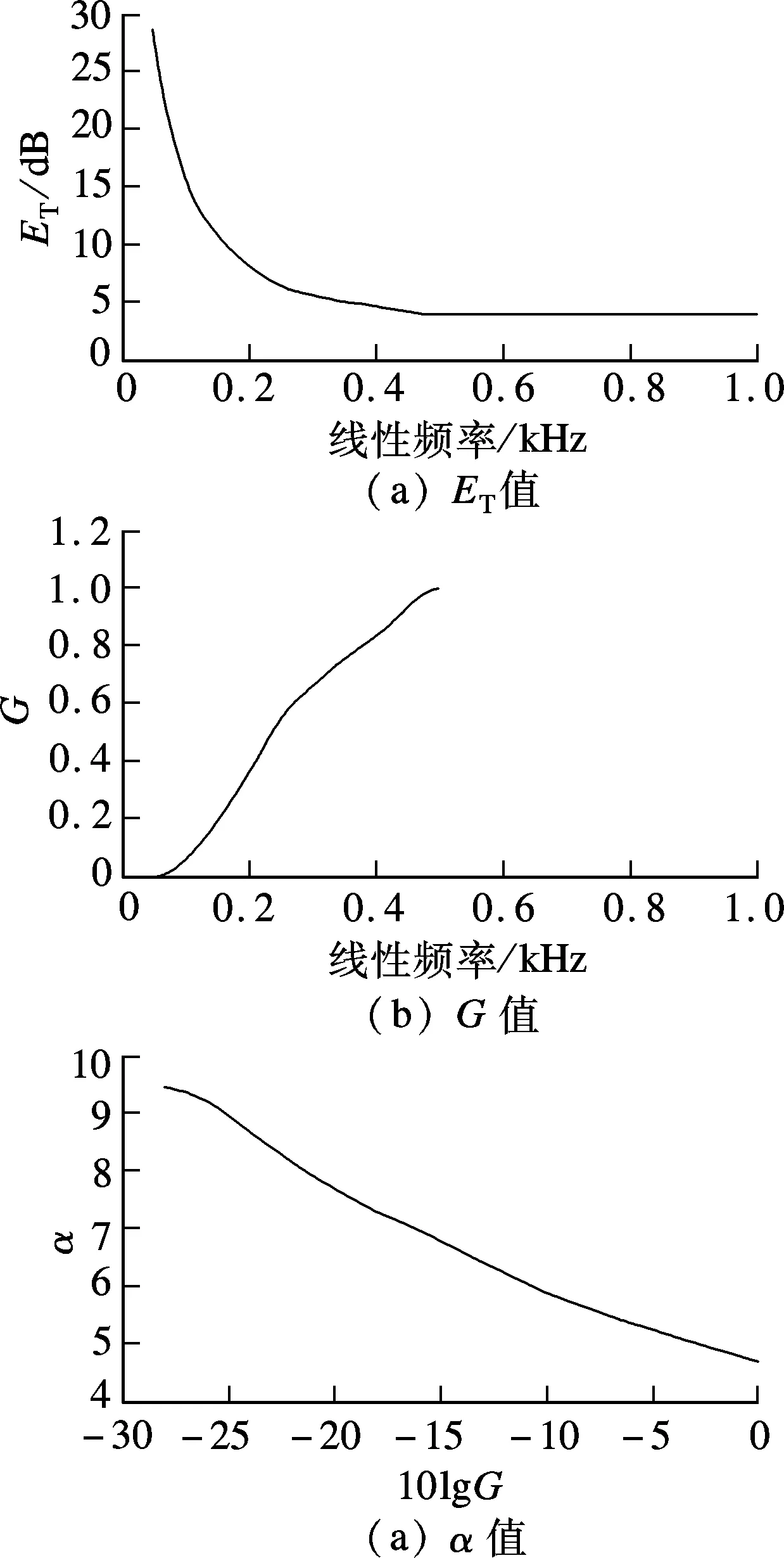
图1 ET,G值和α值的示意图

根据以上计算步骤,可以得到372个特性响度值,总响度就等于这些特性响度之和,即

(6)

根据上述Moore响度的计算方法,可看出响度是声音信号幅度和频率的函数,与幅度变化有很大关系．在心理声学特征中,相同响度情况下,通过音色可以很好地区分信号.在声纳员听音判型中,响度和音色是紧密联系的,下面从音色特征研究舰船辐射噪声的音色模型．

2 舰船辐射噪声的音色模型

在声音响度相同的情况下,音色特征能有效地区分声音信号．螺旋桨的桨拍声以轻重变化为主要特点,音色就是在这种轻重拍的发生、发展、衰变到二者交替轮换中展现出来的动态特性[1]．每种乐器都有其固有的频率范围,产生基频和基频谐音,带来不同的音色,而桨拍声是不同结构的螺旋桨击水的声音．不同的船或不同的工况,比如桨的尺寸、桨轴功率、转速等不同,螺旋桨击水时具有不同的谐振频率,相应产生的基音和谐音不同,从而产生音色差别．在乐音中,谱质心是描述声音信号的频率分布和能量分布的信息．当声音集中在高频时,声音明亮、清晰、有光泽,相反在低频,声音暗、闷、不美[1]．谱质心的物理含义是声音能量集中的区域,在频率分析范围内,将谱能量函数看成是频率的概率密度函数,谱质心便是频率的一阶矩,基于一维的谱质心不能区分目标,因此提出了动态频带的多维谱质心特征提取方法[9].本文在谱质心的基础上研究二阶、三阶和四阶中心矩,即谱质心带宽、谱质心斜度和谱质心峰度,并推广到分段频段的谱质心、谱质心带宽、谱质心斜度和谱质心峰度,从而研究舰船辐射噪声的音色特征模型．

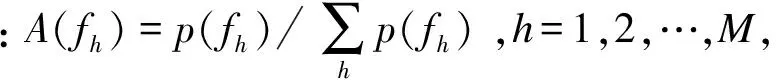
(7)

(8)

(9)

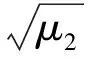
为更好地理解其物理含义,用3个不同频率、不同声压级的正弦信号的合成声音进行说明:① 60dB、500Hz和60dB、1000Hz的正弦信号合成声音;② 60dB、500Hz和60dB、800Hz的正弦信号合成声音;③ 60dB、500Hz和63dB、1000Hz的正弦信号合成声音．由式(7)～(9)求得3个正弦合成声音的一维谱质心分别是750,650和833Hz,一维谱质心带宽分别为250,150和222.5Hz,一维谱质心斜度分别为0, 0和2820.6,一维谱质心峰度分别为62497,22497和91413．谱质心反映信号能量集中的频率区域,由上述正弦合成声音,可知谱质心与声音信号的基频有很大关系：当分音的幅度不变时,随着频率的下降谱质心有所下降；当分音频率不变时,谱质心靠近幅度最大的分音对应的频率值．谱质心带宽是能量分布概率的方差,反映信号能量集中的频率成分所占的带宽,谱质心带宽受声音信号的频率和幅度共同影响：当分音的幅度不变时,随着分音频率下降谱质心带宽相应有所下降；当分音的频率不变、幅度发生变化时,谱质心带宽要小于幅度变化前的谱质心带宽．谱质心斜度的值为零时,其能量概率密度函数是对称分布的．谱质心峰度反映信号能量分布偏离对称分布的歪斜程度,越接近对称分布,其值越接近零．

3 仿真验证

舰船辐射噪声时变功率谱的简化模型如下[10]:

G(t,w)=[1+m(t)]Gx(w)+Gl(w)

(10)

其中SL=112+50log(v/10)+15log(DT),航速v为10kn,吨位DT为10kt．Gl(w)是线谱,线谱时域信号仿真模型为

其中，Ak高出连续谱10～25dB；fk=mns,m为谐波次数,n为叶片数,s为转速(r/s)．

上述舰船辐射噪声的时变功率谱的采样频率为22.5kHz,n为4.由于人耳对声音响度的分辨率为0.01s,每一帧取为0.01s,观测1s内的归一化功率.根据上述的Moore响度计算方法计算Moore响度,并观测1s内的归一化Moore响度变化,4种模式的归一化功率和响度见图2.

对海上实际数据进行仿真,采样频率为22.5kHz,每一帧取为0.01s,经过大量的数据统计,发现0.6s内3类目标A,B,C的Moore响度变化如图3所示．

由图2可看出响度主要由功率谱密度的幅度决定,即主要受m(t)的影响,因此舰船辐射噪声的响度随着时间的变化而出现缓慢变化的周期效应.将舰船辐射噪声按照0.01s进行分帧,并对分帧的Moore响度值进行平均,最后将Moore响度均值作为响度特征．

图2 均匀模式和非均匀模式的归一化功率和响度变化图

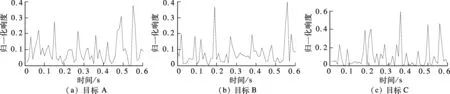
图3 3类目标分帧Moore响度变化曲线

针对海上实际数据,截取1s内的数据作为样本信号,分别得到3类目标基于六分段频带的谱质心、谱质心带宽、谱质心斜度和谱质心峰度的分布图,如图4所示．从图中可看出,六分段的谱质心、谱质心带宽、谱质心斜度和谱质心峰度有一定的区分度．

将Moore响度的均值作为一维特征,顺序排列六分段频带的谱质心、谱质心带宽、谱质心斜度和谱质心峰度值,一共组成25维特征．依据一定的样本,统计3类目标A,B,C的25维特征,并计算特征的均值和方差,如图5所示．从图中可看出,3类目标的均值差异大,方差较小,特征集中度较好,证明组合的25维特征是较为稳健的．

图4 3类目标的六分段谱质心、谱质心带宽、谱质心斜度和谱质心峰度分布图

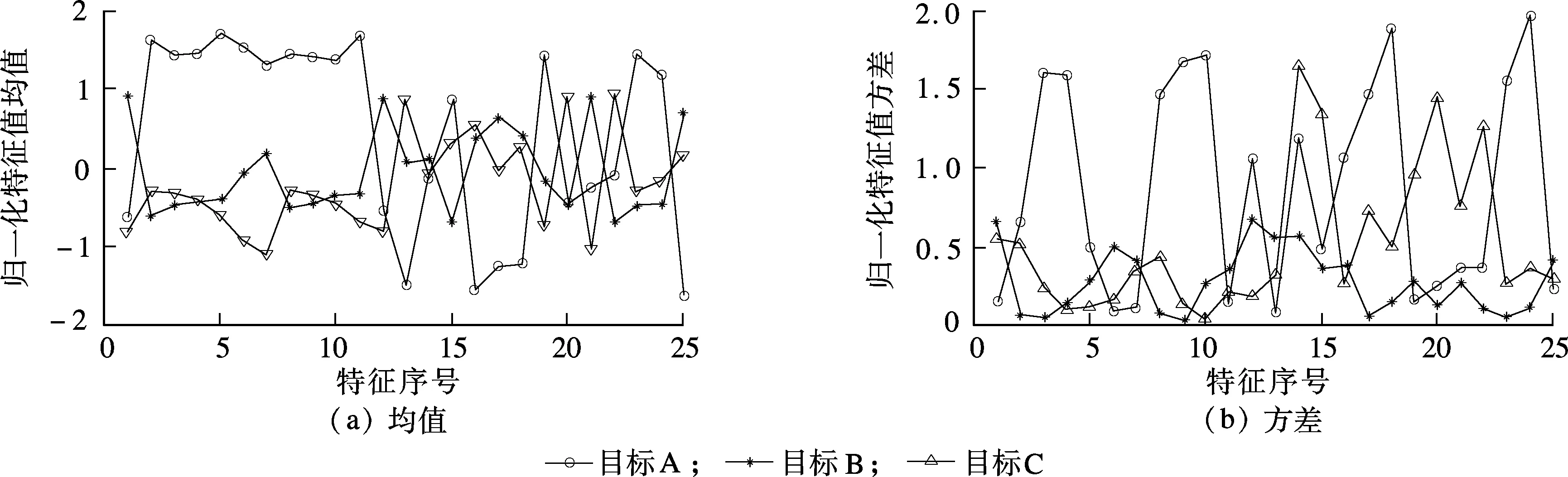
图5 3类目标25维特征的均值和方差分布图

提取3类目标的响度和音色一共25维特征作为目标分类的识别特征,对130个样本进行试验,验证特征提取方法的有效性．分类器采用BP神经网络分类器,结构层数为3层,隐含层的层数为10,采用批处理方法,试验结果如表1所示．从表1可看出,将Moore响度和音色一共25维特征作为识别特征,其目标识别率较高,表明提取目标的响度和音色特征矢量作为识别特征对目标进行分类是有效的．

表1 3类目标的识别率

4 结语

声纳员听音判型是一种有效的目标识别方法,建立相应的数学模型是研究难点．本文基于舰船辐射噪声的仿真模型研究Moore响度的变化规律,将Mooer响度均值作为一维特征,并在谱质心数学定义的基础上推导谱质心带宽、谱质心斜度和谱质心峰度的公式．由于一维的谱质心很难区分目标,因此提出基于分段频带的谱质心、谱质心带宽、谱质心斜度和谱质心峰度的音色特征模型．分析基于Moore响度和音色特征模型相结合的特征的均值和方差,得出这25维特征具有一定的稳健性,进一步将其应用于目标识别中,实验结果表明这一特征提取方法是有效的．实际中,鉴于目标声学特性的复杂多变性,本方法的稳健性还有待进一步研究．

)

[1]刘载芳, 王大训, 张友奎. 声纳听音判型 [M]. 北京: 海军出版社,1999.

[2]Park T H. Automatic musical instrument recognition [D]. Tampere, Finland: Tampere University of Technology, 2001.

[3]Giulio A, Maurizio L, Emanuele P. Musical instrument timbres classification with spectral features [J].JournalonAdvanceinSignalProcessing, 2003,2003(1): 5-14.

[4]Xin Z, Zbigniew W. Analysis of sound features for musical timbre recognition [C]//InternationalConferenceonMultimediaandUbiquitousEngineering. Seoul,Korea, 2007: 26-28.

[5]王娜, 陈可安. 水下噪声音色属性回归模型以及在目标识别中的应用[J]. 物理学报, 2010, 59(4): 2873-2881.

Wang Na, Chen Ke’an. Regression model of timbre attribute for underwater noise and its application to target recognition [J].ActaPhysicaSinica, 2010,59(4): 2873-2881. (in Chinese)

[6]Zwicker E, Fastl H.Psychoacoustics:factsandmodels[M]. 2nd ed. Berlin: Spring-Verlag, 1999: 204-237.

[7]Moore B C J, Glasberg B R,Baer T. A model for the prediction of thresholds, loudness, and partial loudness [J].AcousticalSocietyofAmerica, 1997,45(4): 224-239.

[8]Moore B C J. ANSE S3.4-2005 Procedure for the computation of loudness of steady sounds [S]. New York: American National Standards Institute, 2005.

[9]王娜, 陈克安. 分段谱质心特征在水下目标识别中的应用[J]. 兵工学报, 2009, 30(2): 144-149.

Wang Na, Chen Ke’an. Application of sub-band spectral centroid features to recognition underwater targets [J].ActaArmamentarii, 2009,30(2): 144-149. (in Chinese)

[10]钱晓南. 舰船螺旋桨噪声 [M]. 上海:上海交通大学出版社, 2011.