布尔函数与形态算子关系的研究
2013-12-22段汕,罗敬,徐文,贺兴
段 汕,罗 敬,徐 文,贺 兴
(中南民族大学 数学与统计学学院,武汉 430074)
数学形态学用于图像处理的基本思想,是用一个作为结构元素的“探针”去探测输入图像,以便考察图像各个部分的相互关系,了解图像的结构特征[1].数学形态学的基本运算是基于集合的观点,因此形态算子的性能将主要以几何的方式进行刻画.但是随着形态学应用领域的不断发展,在很多实际问题中,数学形态学所定义的形态算子不能满足应用领域的需求,因此需要从基础理论入手寻找解决问题的新出路和新方法.笔者认为从代数理论的角度研究形态算子,探讨布尔函数与形态变换的关系,有助于提高形态算子的性能,将为多种形式、基于不同空间结构的形态变换给出一个统一的理论框架,有利于形态算子的应用以及新算法的研究.
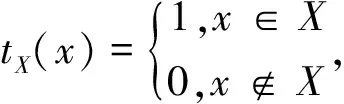
1 预备知识
数学形态学的基本定理最终被简化到完备格结构[5,6],使得完备格结构成为图像空间最基本的代数结构,格的完备性理论则成为形态分析方法最为重要的理论基础.结构形式最为简单的布尔格是只含有0和1两个元素的集合{0,1},取值于集合{0,1}的变量称为布尔变量.布尔变量u,v的基本运算(下确界运算,上确界运算,及余运算)定义如下:
u∧v=u·v=min(u,v),

由集合{0,1}可以生成n元布尔向量的集合,记为{0,1}n={u=(u1,…,un),ui∈{0,1}},利用完备格的理论,该集合在以下所定义运算的基础上构成布尔格:
(1)u·v=(u1v1,…,unvn)=u∧v;
(2)u+v=(u1+v1,…,un+vn)=u∨v;
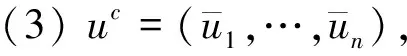

若b为含有n元变量的布尔函数,对于任意的布尔变量u,v,如果u≤v,有b(u)≤b(v)成立,则b为增性的;如果b(1)=1且b(uv)=b(u)b(v),则b为乘性的;如果b(0)=0且b(u+v)=b(u)+b(v),则b为加性的.
对于二值图像X,结构元素A,联合二值图像的特征函数tX与n元布尔函数b定义一个结构化的映射ΨA,b:p(Ed)→p(Ed),记为:
ΨA,b(X)={h∈Ed:b(tX(a1+h),…,
tX(an+h))=1},
从ΨA,b定义可以看出,ΨA,b的性质依赖于结构元素A和所选取的布尔函数b.
2 ΨA,b的基本性质
二值形态变换中最基本的运算是腐蚀和膨胀,这两种基本的运算都具有平移不变性,则可以证明ΨA,b也具有平移不变性.
性质1(平移不变性) 对于给定的结构元素A和布尔函数b,ΨA,b关于二值图像X具有平移不变性,即有:ΨA,b(Xα)=[ΨA,b(X)]α,α∈Ed为平移矢量.
证明由定义可得[ΨA,b(X)]α={h∈Ed:b(tX(a1+h),…,tX(an+h))=1}α,根据集合的平移性得:[ΨA,b(X)]α={α+h∈Ed:b(tX(a1+h),…,tX(an+h))=1},令h′=h+α可得:
[ΨA,b(X)]α={h′∈Ed:b(tX(a1+h′-α),…,tX(an+h′-α))=1},
根据集合平移性tX(ai+h′-α)=tXα(ai+h′),其中i=1,2,3,…,n,则有:
[ΨA,b(X)]α={h′∈Ed:b(tXα(a1+h′),…,tXα(an+h′))=1}=ΨA,b(Xα),因此ΨA,b具有平移不变性.
由ΨA,b的定义知,结构元素A为ΨA,b一个有限窗.关于ΨA,b在文献[4]中有以下结论:
引理1[4]ΨA:p(Ed)→p(Ed)为一个平移不变的有限窗算子[4],窗为:A={a1,a2,…,an}.n元布尔函数b定义为:b(u1,u2,…,un)=[0∈Ψ({ai|ui=1})],则有:ΨA=ψA,b.
性质2 对于给定的布尔函数b,结构元素与二值图像之间具有以下平移的关系,即有
ΨAα,b(X)=ΨA,b(X-α),其中Aα={ai+α|ai∈A},X-α={x-α|x∈X}.
证明由ΨAα,b(X)={h∈Ed:b(tX(a1+α+h),…,tX(an+α+h))=1},根据引理1可得b(tX(a1+α+h),…,tX(an+α+h))=1,由集合平移性tX(ai+α+h)=tX-α(ai+h),i=1,2,…,n,则b(tX-α(a1+h),…,tX-α(an+h))=1,故有:
ΨAα,b(X)={h∈Ed:b(tX-α(a1+h),…,tX-α(an+h))=1}=ΨA,b(X-α),
故ΨAα,b(X)=ΨA,b(X-α)成立.
对于ΨA,b与b的相关性,有以下性质3.
性质3 (1)ΨA,∨i∈Ibi(X)=∨i∈IΨA,bi(X) ; (2)ΨA,∧i∈Ibi(X)=∧i∈IΨA,bi(X) ;(3)(ΨA,b)*(X)=ΨA,b*(X) ,其中I为指标集[7].
证明(1)设h∈Ed,对于任意的h∈ΨA,∨i∈Ibi(X),则有
ΨA,∨i∈Ibi(X)={h∈Ed:∨i∈Ibi(tX(a1+h),…,tX(an+h))=1},
根据引理1可得:∨i∈Ibi(tX(a1+h),…,tX(an+h))=1,由布尔函数的基本性质则存在i0∈I,使得bi0(tX(a1+h),…,tX(an+h))=∨i∈Ibi(tX(a1+h),…,tX(an+h))=1,其中I为指标集,则有ΨA,bi0(X)=ΨA,∨i∈Ibi(X),又因为ΨA,bi0(X)⊆∨i∈IΨA,bi(X),故有h∈∨i∈IΨA,bi(X);设h∈Ed,对于任意的h∈∨i∈IΨA,bi(X),则有:
∨i∈IΨA,bi(X)=∨i∈I{h∈Ed:bi(tX(a1+h),…,tX(an+h))=1},由集合的性质和ΨA,b的定义知,存在i0∈I,使得∨i∈IΨA,bi(X)=ΨA,bi0(X),根据引理1可得bi0(tX(a1+h),…,tX(an+h))=1,由布尔函数的上确界运算可知:
bi0(tX(a1+h),…,tX(an+h))≤∨i∈Ibi(tX(a1+h),…,tX(an+h)),
则有∨i∈Ibi(tX(ai+h))=1,故可得h∈ΨA,∨i∈Ibi(X),则(1)成立.
(2)设h∈Ed,对于任意的h∈ΨA,∧i∈Ibi(X),
则有:
ΨA,∧i∈Ibi(X)={h∈Ed:∧i∈Ibi(tX(a1+h),…,
tX(an+h))=1},
根据引理1可得:∧i∈Ibi(tX(a1+h),…,tX(an+h))=1,由布尔函数的基本性质,则存在i0∈I,使得∧i∈Ibi(tX(a1+h),…,tX(an+h))=bi0(tX(a1+h),…,tX(an+h))=1,其中I为指标集,则可得ΨA,∧i∈Ibi0(X)=ΨA,bi0(X),由布尔函数的下确界运算可知:
∧i∈Ibi(tX(a1+h),…,tX(an+h))≤
bi(tX(a1+h),…,tX(an+h)),
即对于任意的i∈I,有bi(tX(a1+h),…,tX(an+h))=1成立,故h∈ΨA,bi(X),表明对于任意的i∈I,有ΨA,bi0(X)⊆ΨA,bi(X)成立,由集合的基本性质可得:ΨA,bi0(X)⊆∧i∈IΨA,bi(X),故有h∈∧i∈IΨA,bi(X);
设h∈Ed,对于任意的h∈∧i∈IΨA,bi(X),由集合的性质和ΨA,b的定义知,存在i0∈I,使得∧i∈IΨA,bi(X)=ΨA,bi0(X),即对于任意的i∈I,有ΨA,bi0(X)⊆ΨA,bi(X)成立,由引理1可得:bi0(tX(a1+h),…,tX(an+h))≤∧i∈Ibi(tX(a1+h),…,tX(an+h)),已有∧i∈IΨA,bi(X)=ΨA,bi0(X)成立,根据引理1可得:bi0(tX(a1+h),…,tX(an+h))=1 ,综上可得:ΨA,bi0(X)⊆ΨA,∧i∈Ibi(X),故h∈ΨA,∧i∈Ibi(X),故(2)成立;
(3)对于任意的h∈(ΨA,b)*(X),由定义可得 (ΨA,b)*(X)=[ΨA,b(Xc)]c,其中Xc为集合X的补集,故可得:[ΨA,b(Xc)]c={h∈Ed:b(tXc(a1+h),…,tXc(an+h))=1}c,由集合的性质和布尔函数的基本性质有[ΨA,b(Xc)]c={h∈Ed:b(tXc(a1+h),…,tXc(an+h))=0},由布尔函数的基本性质
[ΨA,b(Xc)]c=
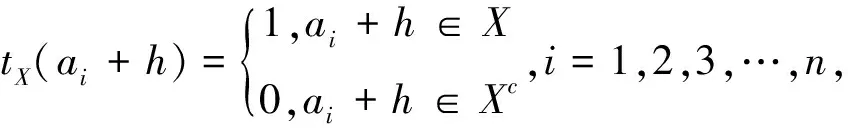
上述性质证明过程可以看出,对于给定的结构元素A和二值图像X,ΨA,b的上确界运算、下确界运算及余运算,与布尔函数的上确界运算、下确界运算及余运算是保持一致的.
对于给定的结构元素,腐蚀和膨胀都具有增性,可以证明ΨA,b也具有增性.
性质4 (增性)ΨA,b是增性的充分必要条件是布尔函数b也是增性的.
证明必要性.设X,Y⊆Ed且满足X⊆Y,对于任意的:
h∈ΨA,b(X)={h∈Ed:b(tX(a1+h),…,tX(an+h))=1},
由引理1可得b(tX(a1+h),…,tX(an+h))=1,因为X⊆Y,故有tX(ai+h)≤tY(ai+h),其中i=1,2,3,…,n,又因为b为增的,则b(tY(a1+h),…,tY(an+h))=1,所以有h∈ΨA,b(Y),故有ΨA,b(X)⊆ΨA,b(Y)成立;
充分性.当ΨA,b为增的,设X,Y⊆Ed且满足X⊆Y,那么有ΨA,b(X)⊆ΨA,b(Y)成立.反证法:若b为非增的,对于任意的h∈ΨA,b(X),有b(tX(a1+h),…,tX(an+h))=1,因为X⊆Y,故有tX(ai+h)≤tY(ai+h),i=1,2,3,…,n,又因为b为非增的,则b(tY(a1+h),…,tY(an+h))≤1,若当b(tY(a1+h),…,tY(an+h))=0时可知h不属于ΨA,b(Y),这与题设矛盾,故原命题成立.
3 布尔函数与形态变换的关系
利用ΨA,b以上的性质,通过选取适当性质的布尔函数,研究其与形态变换(腐蚀、膨胀)之间的关系,并获得形态变换的表达式.
命题1 对于给定的结构元素A和n元布尔函数b,(1)ΨA,b是腐蚀的充分必要条件是b是乘性的布尔函数;(2)ΨA,b是膨胀的充分必要条件是b是加性的布尔函数.
证明(1)必要性.设h∈Ed,对于任意的h∈ΨA,b(∧i∈IXi),由引理1可得:b(t∧i∈IXi(a1+h),…,t∧i∈IXi(an+h))=1,又因为b为乘性的布尔函数,故有:∧i∈Ib(tXi(a1+h),…,tXi(an+h))=1,即对于任意的i∈I,都有b(tXi(a1+h),…,tXi(an+h))=1,则h∈∧i∈IΨA,b(Xi),故ΨA,b(∧i∈IXi)⊆∧i∈IΨA,b(Xi);同理可证∧i∈IΨA,b(Xi)⊆ΨA,b(∧i∈IXi);综上有∧i∈IΨA,b(Xi)=ΨA,b(∧i∈IXi)成立;
充分性.若ΨA,b为腐蚀,由腐蚀的定义可得:ΨA,b(∧i∈IXi)=∧i∈IΨA,b(Xi),设Xi⊆Ed,对于任意的h∈ΨA,b(∧i∈IXi),由引理1可等价为:b(t∧i∈IXi(a1+h),…,t∧i∈IXi(an+h))=1,因为ΨA,b(∧i∈IXi)=∧i∈IΨA,b(Xi),故h∈∧i∈IΨA,b(Xi),由∧i∈IΨA,b(Xi)的定义和引理1 等价为:∧i∈Ib(tXi(a1+h),…,tXi(an+h))=1,故有以下等式成立:
b(t∧i∈IXi(a1+h),…,t∧i∈IXi(an+h))=
∧i∈Ib(tXi(a1+h),…,tXi(an+h))=1,
即满足b(uv)=b(u)b(v);对于任意的h∈ΨA,b(X),由引理1可得:b(tX(a1+h),…,tX(an+h))=1,又因为ΨA,b(X)为腐蚀,则有Ah⊆X,即对于任意的ai,i=1,2,3,…,n,都有ai+h∈X,则所有tX(ai+h)=1,得b(1)=1,由定义可得b为乘性的.
(2)必要性.设h∈Ed,对于任意的h∈ΨA,b(∨i∈IXi),由引理1可得:b(t∨i∈IXi(a1+h),…,t∨i∈IXi(an+h))=1,又因为b为加性的布尔函数,故有:∨i∈Ib(tXi(a1+h),…,tXi(an+h))=1,必存在i0∈I,使得b(tXi0(a1+h),…,tXi0(an+h))=1,故h∈ΨA,b(Xi0),又因为ΨA,b(Xi0)⊆∨i∈IΨA,b(Xi),故ΨA,b(∨i∈IXi)⊆∨i∈IΨA,b(Xi);同理可证∨i∈IΨA,b(Xi)⊆ΨA,b(∨i∈IXi),综上有∨i∈IΨA,b(Xi)=ΨA,b(∨i∈IXi)成立;
充分性.若ΨA,b为膨胀,即有ΨA,b(∨i∈IXi)=∨i∈IΨA,b(Xi),设Xi⊆Ed,由ΨA,b(∨i∈IXi)的定义和引理1可得:b(t∨i∈IXi(a1+h),…,t∨i∈IXi(an+h))=1,因为ΨA,b(∨i∈IXi)=∨i∈IΨA,b(Xi),则根据∨i∈IΨA,b(Xi)定义和引理1可得:∨i∈Ib(tXi(a1+h),…,tXi(an+h))=1,故有以下等式成立:
b(t∨i∈IXi(a1+h),…,t∨i∈IXi(an+h))=
∨i∈Ib(tXi(a1+h),…,tXi(an+h))=1,
即满足b(u+v)=b(u)+b(v);对于任意的h∉ΨA,b(X),根据引理1可得:b(tX(a1+h),…,tX(an+h))=0,由ΨA,b(X)是膨胀且h∉ΨA,b(X),则有Ah∩X=∅,即对于任意的ai∈A,i=1,2,3,…,n,都有ai+h∉X,即所有的tX(ai+h)=0,得b(0)=0,则b为加性的.
文献[4]中有以下结论.
结论1 任何一个乘性的布尔函数b可以表示成如下形式:
b(u1,u2,…,un)=(c1+u1)(c2+u2)…
(cn+un),ci∈{0,1}.
(1)
结论2 任何一个加性的布尔函数b可以表示成如下形式:
b(u1,u2,…,un)=c1u1+c2u2+…+cnun,
ci∈{0,1}.
(2)
根据命题1和文献[4]中已有结论可知:
结论3 在(1)式中,取ci=0,∀i=1,2,3,…,n,则有b(u1,u2,…,un)=u1·u2·…un,令ui=tX(ai+h),其中ai∈A,可得ΨA,b(X)表达式为:
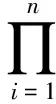
(3)
结论4 在(2)式中,取ci=0,∀i=1,2,3,…,n,则有b(u1,u2,…,un)=u1+u2+…+un,令ui=tX(ai+h),其中ai∈A,可得ΨA,b(X)表达式为:
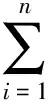
(4)
以上研究表明二值形态变换可以通过选取适当性质的布尔函数进行描述,但是从(3)式表示的腐蚀和(4)式表示的膨胀可以看出,两种运算只考虑了(1)式中所有ci=0和(2)式中所有ci=1的特殊情况,而对其它的情况没有作讨论.当考虑(1)式中,部分ci=0时,则有b(u1,u2,…,un)=u1·u2·…·us,其中1≤s≤n,根据文献[4]中秩函数rs的定义,则有:
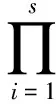
由命题1知ρA,rs也是腐蚀运算.从形式上看,ρA,rs表示的腐蚀运算比经典的腐蚀运算更具一般性,将为扩展二值形态变换提供新的途径,同时也为形态学应用算法的研究提出了一种新的思路.
4 结束语
本文从代数理论入手,引入一个结构化映射,通过选取适当性质的布尔函数描述形态变换,将基于集合定义的形态变换扩展到基于结构化映射表示的形态变换,为形态变换的扩展提供了新的途径,也为今后扩充一类具有形态变换形式的广义形态算子,以及从结构化的角度描述形态变换的代数结构及代数表现形式提供理论依据[8,9],此外对形态变换在图像处理中的应用也具有一定的指导意义.
[1]崔 屹.图像处理与分析——数学形态学方法及应用[M].北京:科学出版社,2000:1-2.
[2]Goutsias J,Schonfeld D.Morphological representation of discrete and binary image [J].IEEE Transactions on Signal Processing,1991,39(6):1369-1379.
[3]段 汕.形态学及其在遥感影像处理中的应用研究[D].武汉:武汉大学,2004.
[4]Heijmans H.Morphological image operator [M].Boston: Academic Press,1994:17-102.
[5]Shin F R.Image processing and mathematical morphology fundamentals and applications[M].New York: CRC Press,2009:5-8.
[6]Kresch R.Mathematical morphology on complete semilattices and its application to image processing [J].Fund Inform,2000,41(1-2):33-56.
[7]周民强.实变函数论[M].北京:北京大学出版社,2008:2-3.
[8]Heijmans H,Boomgaard R.Algebraic framework for linear and morphological scale-space [J].Visual Communication and Image Representation ,2002,13(1-2): 269-301.
[9]Heijmans H ,Keshet R.First steps toward self-dual morphology [C]//IEEE.IEEE Int′ l Corf on Image Processing.Vancouver : IEEE ,2000(2):934-937.
