基于ANP与vague集的工程项目风险评价方法改进

2013-12-21易欣

华东交通大学学报 2013年2期

易欣

（华东交通大学土木建筑学院，江西南昌330013）

一方面，随着我国经济快速发展和综合国力的不断增强，越来越多的新建项目都呈现出规模大、难度高、工期长、参与单位多等复杂性特点，再加上环境因素等其他方面的影响，使得项目存在着高度的不确定性，具有很大的风险。另一方面，这些工程项目管理却普遍存在进度滞后、投资超限等问题，这既与项目自身复杂性与日俱增有关，更多的却往往来自项目参与各方，尤其是业主对工程项目风险管理的不够重视。项目风险管理的知识告诉我们，在项目决策阶段进行有效的风险评估工作，不但对项目的成功与否影响最大，而且代价最小。为了尽量降低风险因素造成项目实施阶段的失控，确保项目的经济效益，加强工程项目风险管理势在必行，而做好风险管理的关键是进行有效的风险评价。

风险无处不在，风险无时不有。工程项目的风险评估方法一直是国内外学术界关注的热点：李海凌等［1］将层次分析法应用在工程项目风险评价中，武乾等［2］提出工程项目风险模糊综合评价方法，贺剑平等［3］从承包商角度使用层次分析法进行风险评价，李亮等［4］将灰色关联和层次分析法组合起来用于工程项目风险综合评价，曹丽［5］运用人工神经网络进行了工程项目风险风险分析。此外，常见的工程项目风险分析方法还有调查打分法、敏感性分析和蒙特卡罗模拟等［6］。上述方法对提高我国工程项目风险管理水平起到了很大作用，但这些方法假设各风险因素完全独立，忽视了它们之间的相互影响和作用可能导致结果失真。Saaty［7］提出的网络分析法ANP（analytic network process）可以很好地解决这个问题，该方法相同或不同层级的因素之间可以是支配或反馈的关系，更符合实际，分析结果也更加准确。另外，工程项目风险评价存在大量的不确定数据和不完全信息，属于典型的模糊多属性决策问题。Gau和Buehrer提出的vague集［8］是对Zadeh模糊理论的进一步推广，它对模糊信息的分析处理较普通模糊集更强大、更灵活也更准确。本文基于vague集理论与网络分析法，从业主角度提出了工程项目风险定量评估新的方法，以期既能改善我国目前工程项目管理绩效，也可为业主或政府部门进行科学决策提供更加有效的依据，希望研究成果能够进一步拓宽我国工程项目管理学科的研究方向。

1 工程项目的风险因素辨识

风险辨识是风险定量评估的基础，而要做好风险因素的识别需要准确理解现代工程项目发展趋势和呈现出的主要特点。复杂性是现代工程项目目前最突出的特征，尽管从多维度工程属性来描述工程项目复杂性的具体情况难免存在一定差异，但它们的复杂性内涵总是相似的。换而言之，工程项目虽然千差万别，但影响这些项目的风险因素总是相似的，主要来自于其规模大、周期长、技术难和环境复杂等特点。根据当前工程项目的主要特点，本文在遵循了客观和可操作性原则，依据相关工程调查报告、勘测设计资料等，参照了国内外相关研究文献［9-10］并结合专家意见，识别出政策风险、管理风险、环境风险、自然风险、人为风险和技术风险等7个主要风险源及其次要风险因素，所得风险清单如表1所示。

表1 工程项目的风险因素清单Tab.1 Risk factor list of construction project

2 风险因素的相应赋权

由于各风险因素对工程项目带来的影响程度是不同的，要准确度量它们对项目风险水平的贡献度时，要通过赋予不同的权重进行表达。表1 所示的风险因素不但组与组之间存在相互影响，而且组内也有关联，例如宏观经济政策变化一般会使当地政府相关制度产生相应变动，而产业结构的调整也会对劳动力市场和材料价格产生影响等。目前常见的各种赋权方法往往忽视了这些因素的相关性，而前述网络分析法可利用直接和间接优势度关系，通过超矩阵对相互关联的因素进行综合分析，可有效地得到综合优势度（权重）。典型的ANP网络由控制层和网络层构成，决策准则认为是完全独立的，而且控制层中可以允许没有决策准则，但必须至少有一个目标。常见的ANP结构如图1所示。

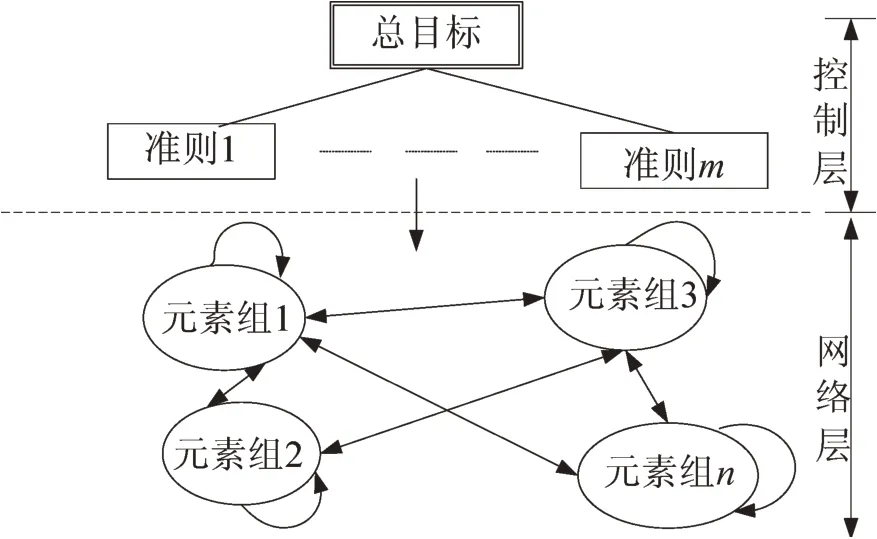
图1 典型的网络分析图结构Fig.1 The typical structural model of ANP

综合优势度（权重）的计算步骤［11］：

1）详细描述待研究问题，确定目标、准则和因素。

2）构建ANP网络。

3）建立无权超矩阵，即以控制层的各准则为主准则，以某因素组中因素为次准则，按照各因素对其他因素的影响程度逐一构造判断矩阵Ws，求出按分块各列归一化的特征向量，依此类推将所得到的所有归一化特征向量汇总到一个矩阵Wij中。

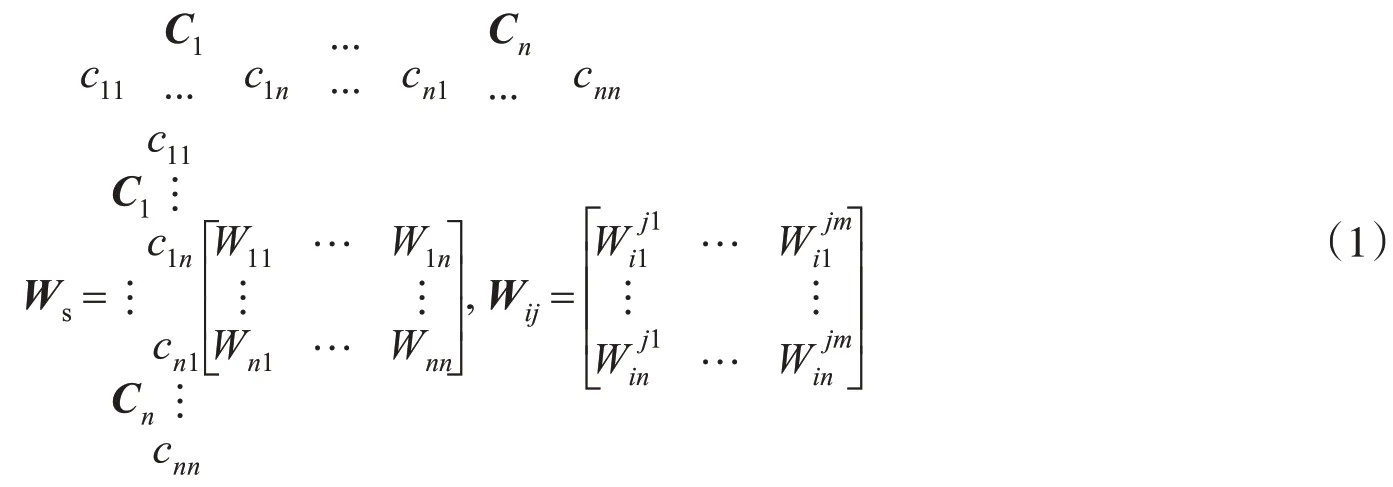
式中：Ci表示各主要风险因素，cij表示其下的各次要风险因素；Wij表示以控制层各元素为准则构造的判断矩阵，这样的矩阵共有m个。Wij由按列归一化后的排序特征向量组成，其列向量表示Ci中的元素对Cj中元素的影响程度排序，若无影响刚为零。

4）求加权超矩阵。虽然各分块已按列归一化了，但却并非是对整个超矩阵按列归一化。因此无权超矩阵中各列的权重之和并不统一，需要通过加权矩阵As进一步做加权处理。加权矩阵As反映的是因素组之间的影响关系，它以控制层的各准则为主准则，以各因素组为子准则，对因素组进行两两比较，构建判断矩阵aj，然后将所求得的特征向量按列归一化后组成，最后只需将加权矩阵As乘以无权超矩阵Ws便得到了加权超矩阵Wsw；

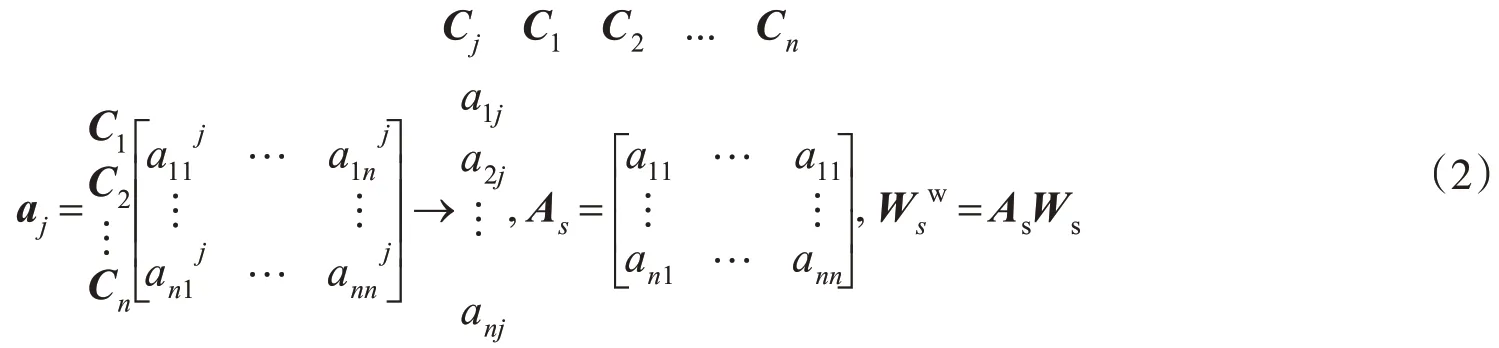
5）求极限超矩阵WsL。由于ANP引入了反馈或依赖关系，故判断两个因素的重要性时，既应直接比较，也要间接比较。这种因素之间复杂的间接关系可通过超矩阵的迭代来反映，这是一个反复迭代然后趋稳的求解程序，类似于马尔科夫过程：

式中：k表示迭代次数。

6）求综合优势度（权重），即对控制层各准则的极限向量按照各准则权重进行汇总并排序。

由于ANP赋权计算是个比较复杂的过程，须先使用1～9标度法对每个因素逐一设定判断矩阵，然后通过计算依次得到无权超矩阵、加权超矩阵和极限超矩阵，最后得到综合优势度（权重），通常使用Super Decisions 软件来完成。本文亦采用此软件对工程项目的风险因素权重求解，先将网络分析图绘出，再邀请专家完成赋权。限于篇幅无法详细列出整个过程，相关输入顺序和输出结果如图2～图5所示。

以此类推，可求出其他准则层下各组内所有因素归一化特征向量，建立起一个无权超矩阵见图4。

再求出加权超矩阵见图5，其录入方法同上。然后，通过软件的Limit Matrix命令求出极限超矩阵，计算结果类似于图4和图5，限于篇幅不再列出。最后，通过Priorities命令求出综合优势度（即权重），将最终计算结果整理后表示如下：

则各风险因素对应的权重向量wi=（0.050 2，0.034 0，0.039 8，0.024 0，0.035 5，0.067 7，0.046 2，0.010 9，0.088 8，0.077 8，0.092 8，0.114 5，0.012 3，0.001 8，0.038 1，0.027 4，0.021 7，0.019 6，0.015 0，0.066 2，0.115 3）T。wi表示各风险因素对应的最终权重向量。如果对计算结果简单分析，发现最大的几个风险因素是技术的适用性、项目周边环境和当地政府，而并非来自自然和政策风险，与我们最初的主观经验判断存在较大差别，我们还能得出一个很有意义的现象，即说明目前影响我国工程项目目标实现的重要原因除了项目自身技术难度之外，更多的往往来自项目的利益相关者，而非项目直接参与者。这也给了我们有益的启示，即现阶段我国工程项目管理的研究重点应该从传统的项目直接参与方，逐步转向对项目的利益相关者。

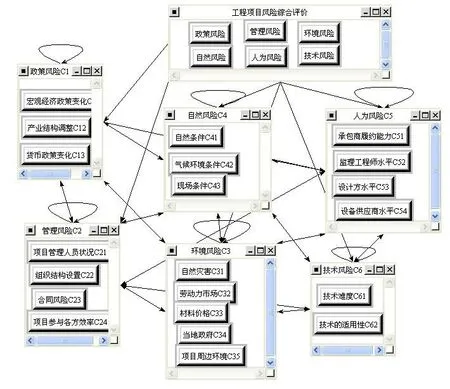
图2 Super Decisions绘制的网络分析图Fig.2 The ANP model plotted by Super Decisions

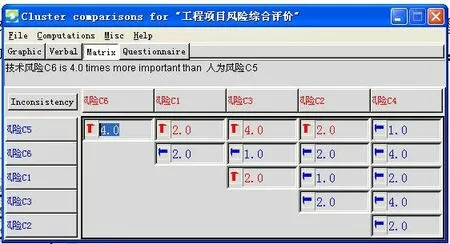
图3 元素组权重计算判断矩阵的录入Fig.3 Judgment matrix data input of cluster

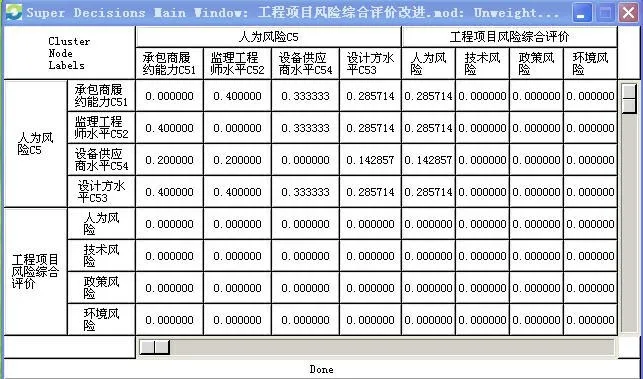
图4 未加权超矩阵的计算结果Fig.4 Calculation result of unweighted super matrix

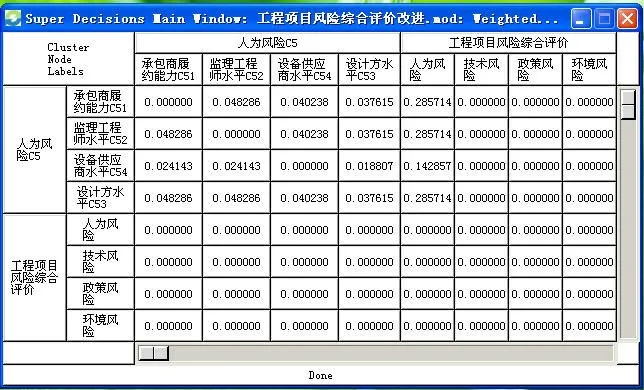
图5 加权超矩阵的计算结果Fig.5 Calculation result of weighted super matrix

3 工程项目风险分析的vague集评价模型

工程项目风险综合评价绝非将各风险因素的简单叠加，而需要进行有效综合分析，由于这个分析过程存在大量的数据和信息不确定和不完全性，因此常常需要使用模糊数学方法来描述风险因素和风险综合度量之间的非线性关系。常见的模糊综合评价法可以很好地解决这个问题，但传统的模糊理论由于隶属度不满足可加性，取大或取小运算则容易丢失中间信息，易导致评价结果的失真。考虑到这一点，本文在此基础上提出了基于vague集理论的改进综合评价方法，下面先对其基本概念进行介绍。

3.1 vague集的基本概念

定义1［12］设U是一个论域，x表示其中任一元素，U中的一个vague集A可用一个真隶属函数tA和一个假隶属函数fA表示，tA(x)是从支持x的证据所导出的x的隶属度下界，fA(x)则是从反对x的证据所导出的x的否定隶属度下界，不确定部分为1-tA(x)-fA(x)。tA(x)和fA(x)将区间［0，1］中的实数与U中的每一个元素联系起来。即：tA(x):U→[0，1]，fA(x):U→[0，1]，为讨论方便，简记tA(x) 为tx，fA(x)为fx。

1）当U是连续的时候，vague集A表示为：A=∫U[tA(x)，1-fA(x)]/xdx，x∈U

2）当U是离散的时候，vague集A表示为：A=[tA(xi)，1-fA(xi)]/xi，xi∈U

上式中：tA(x)+fA(x)≤1，若tA(x)=1-fA(x)，则vague 集退化为Fuzzy集；如果tA(x)和1-fA(x)同时为0或1，则vague集退化为普通集合。

3.2 工程项目风险的vague集综合评价分析步骤

步骤一，对每个风险因素设定相应等级的评语集。评语集是由评审人对风险因素强弱给出的一种语言描述集合。参照工程项目风险管理理论及施工现场实际，本文给出相应评语集=（高风险、较高风险、中等风险、较低风险、低风险）5个等级，同时邀请一定数量的专家选择合适的语言变量来表达评价意见。

步骤二，根据前述网络分析法确定所有风险因素对项目风险影响大小的权重。

步骤三，接着构造vague 集评价矩阵，即请专家按照所给定的评语集对所有因素逐一进行判别，若以Cij(i=1，2，3，4，5，6;j=1，2，3，4，5，)代表其中任一风险因素，设评语集为Vk(k=1，2，3，4，5)，对其构造评价指标体系C和V之间的vague集评价矩阵R为

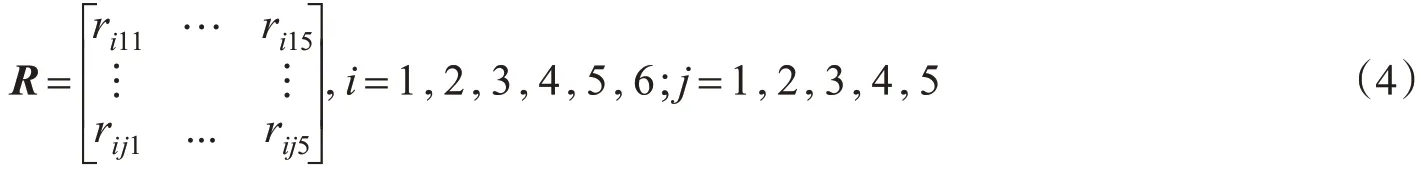
上式矩阵中每一行表示5个评语等级，每一列均对应着每个风险因素对评语集中某个等级的vague集隶属度，rijk表示因素指标Cij对应评语集的相应评价，rijk=[tijk，1-fijk]。组织相关专家针对每个指标按照评语集逐一进行选择，为更真实地表示专家的犹豫程度，允许其选择放弃评价。例如有10位专家对宏观经济政策变化因素评价，若6 人选择了低风险，2 人选了较低风险，1 人选了中等，1 人放弃评价，则r11=(r111，r112，r113，r114，r115)=([0，0.1]，[0，0.1]，[0.1，0.2]，[0.2，0.3]，[0.6，0.7])，其他因素的评语可依此类推。

步骤四，根据风险因素的权重wi和vague集评价矩阵R，对各指标Cij进行基于vague 集的综合评价：

上式中“⊗”为vague集矩阵相乘的运算符号，并且需要用到以下vague集的两个基本公式：

数乘运算：

有限和运算：

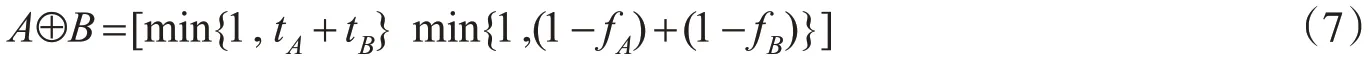
最后，风险评价结果需要按照隶属度最大原则来判定。由于vague 值是一个区间数，可采用Chen 和Tan提出的计分函数［13］来作为vague集的排序规则，公式如下：

对上式的解释是如果想衡量某个候选人满足某个指标要求的程度，可由其真隶属度函数与假隶属度函数的差值来度量，这就如同投票过程中，在人数一定情况下，显然支持的人比反对的人越多就越有优势。因此，根据排序大小即可方便地度量该工程项目的风险水平，还能通过对二级指标分析找到相应的风险源。

4 实证分析

某市拟建一座穿越江底的过江隧道工程，项目静态总投资估算约10亿元，目标工期不超过900个日历天，是该市十二五规划的重点建设项目之一，将对促进当地经济发展起着极为重要的作用。该项目总体地势为北高南低，江底地质构造较复杂。由于项目地处市区，施工对周边交通和百姓生活影响较大。为避免项目的失败，业主希望通过有效地风险评价以确定项目风险水平。为了保证风险评估工作的顺利实施，业主委托咨询机构通过问卷调查向省内高校、专业设计院和省外专家进行函询，将原始数据进行统计和处理后得到了所有风险因素的vague值评价数据如表2所示。

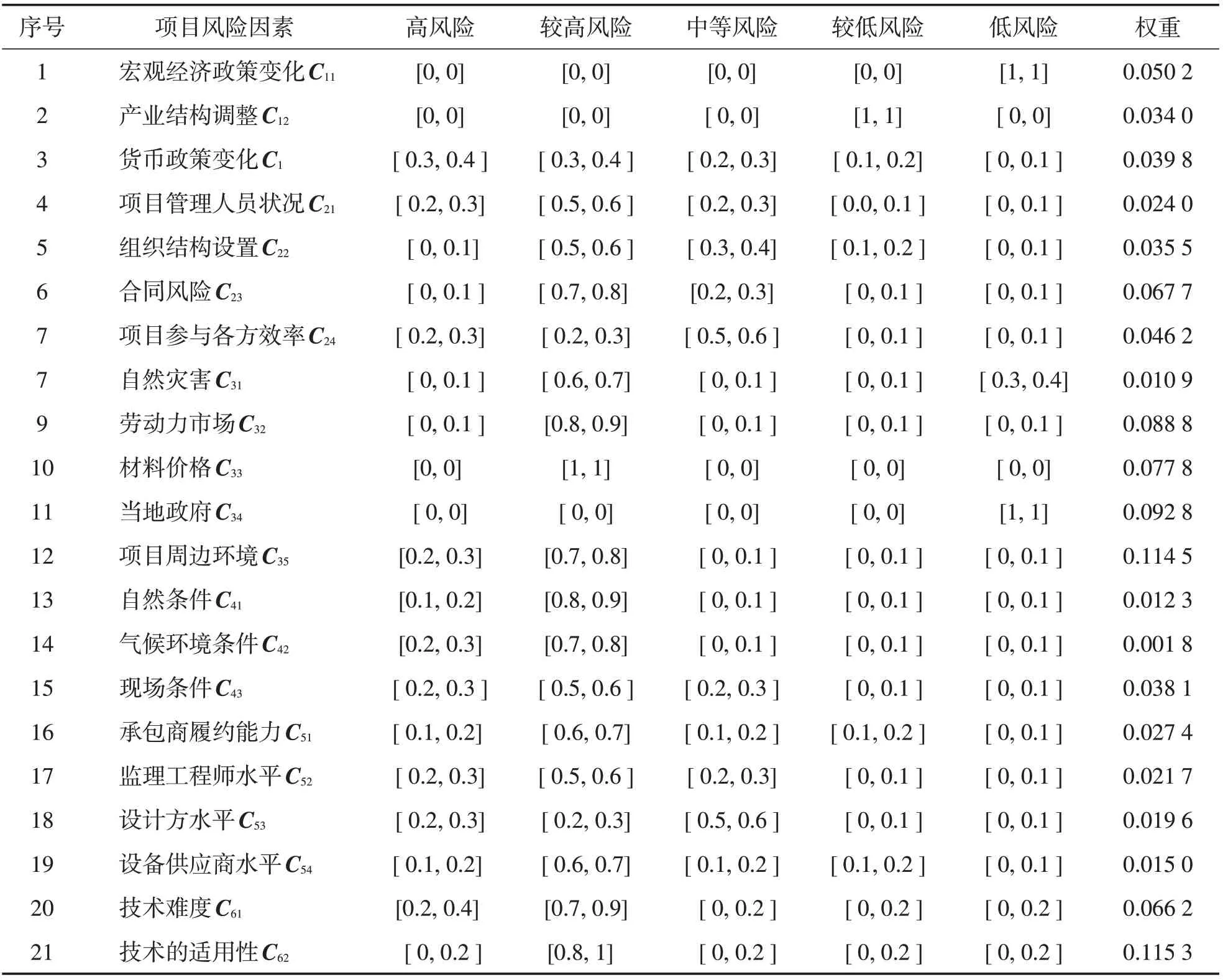
表2 专家对项目各风险因素的vague值评语Tab.2 Expert’s evaluation on each factor of construction project with vague sets

因此，根据式（5）将wi和表2内vague集评价矩阵Ri相乘，遵循式（3）和式（4）的计算规则，便可分别求出该项目对5个风险等级的vague集评价值为：V1=［0，0］⊕［0，0］⊕［0.011 9，0.015 9］⊕［0.004 8，0.007 2］⊕［0，0.003 6］⊕［0，0.006 8］⊕［0.009 2，0.013 9］⊕［0，0.001 1］⊕［0，0.008 9］⊕［0，0］⊕［0，0］⊕［0.022 9，0.034 4］⊕［0.001 2，0.002 5］⊕［0.000 4，0.000 5］⊕［0.007 6，0.011 4］⊕［0.002 7，0.005 5］⊕［0.004 3，0.006 5］⊕［0.003 9，0.005 9］⊕［0.001 5，0.003 0］⊕［0.013 2，0.026 5］⊕［0，0.023 1］=［0.083 8，0.176 5］

同理，求出V2=［0.496 5，0.575 8］，V3=［0.086 1，0.178 7］，V4=［0.045 8，0.138 4］，V5=［0.146 3，0.238 9］，故Vi=（［0.083 8，0.176 5］，［0.496 5，0.575 8］，［0.086 1，0.178 7］，［0.045 8，0.138 4］，［0.146 3，0.238 9］）。最后，根据前述vague集的排序规则可知隶属度的大小顺序为：V2≻V5≻V3≻V1≻V4，所以该项目的风险综合评估为较高。根据风险评估结果，我们还能发现该项目的技术风险、环境风险和自然风险均处于较高水平，同时要特别注意劳动力和材料价格变化对投资控制带来的影响。最终，该项目在经过决策者审慎地集体讨论后放弃，取而代之的是选用了更为成熟、稳妥的桥梁建设方案，并顺利通过了风险评估获得项目立项，从而避免了一旦盲目决策将导致后期建设难以为继，甚至被迫变更的不利境况出现。

5 结语

随着我国新建项目越来越多的出现复杂性特点，为了避免项目后期出现更多难以解决的问题，风险管理对项目科学决策的重要性愈加凸显。而对于工程项目风险管理来说，最重要的步骤就是在项目的期初需要非常审慎、客观并准确地进行风险评估，从风险管理来看这是一个典型的多目标模糊决策问题。在对风险因素对项目影响程度进行衡量时，考虑到这些因素之间的相关性，本文使用了ANP进行分析，很好地提高了计算结果的准确性；同时，由于传统模糊理论存在信息不全面，易损失中间值等不足，引入了具有更全面的信息刻画能力的vague集理论，从而建立了一个科学的工程项目风险定量评价模型。最后通过实例验证了该评估模型的有效性，可以为当前的工程项目风险管理领域提供一种新的定量评价研究方法。

［1］李海凌，宋吉荣.层次分析法在工程项目风险评价中的应用研究［J］.四川建筑，2004（4）：87-90.

［2］武乾，武增海，李慧民.工程项目风险评价方法研究［J］.西安建筑科技大学学报，2006，38（4）：258-260.

［3］贺剑平.层次分析法在承包工程项目风险评价中的应用研究［J］.水利科技与经济，2008（4）：298-300.

［4］李亮，杨俊辉.基于灰色层次分析法的工程项目风险综合评价［J］.西安邮电学院学报，2009，14（4）：121-124.

［5］曹丽.基于人工神经网络的工程项目风险管理研究［D］.西安：西安理工大学，2006.

［6］易欣.基于AHP和蒙特卡罗模拟技术的投标报价风险研究［J］.煤炭经济研究，2009（1）：43-45.

［7］SAATY T L.Decision making with dependence and feedback［M］.Pittsburgh，PA：RWS Publication，1996.

［8］GAU W L，BUEHRER D J.Vague sets［J］.IEEE Trans Systems Man Cybernetic，1993，23：610-614.

［9］赵刚.基于ANP的模糊综合评判法在工程项目风险分析中的应用［J］.河南科学，2009，27（7）：850-853.

［10］李玉钦.基于网络分析法（ANP）的水电工程风险分析方法研究［D］.天津：天津大学，2007.

［11］宫俊涛，刘波等.网络分析法（ANP）及其在供应商选择中的应用［J］.工业工程，2007，10（2）：77-80.

［12］易欣.基于Vague集贴近度的工程项目投资快速估算方法［J］.华东交通大学学报，2012，29（3）：11-15.