车辆-高架桥耦合系统竖向振动分析车辆轨道新模型

2013-12-21罗文俊雷晓燕练松良

华东交通大学学报 2013年2期

罗文俊，雷晓燕，练松良

（1.同济大学道路与交通工程教育部重点实验室，上海201804；2.华东交通大学铁路环境振动与噪声教育部工程研究中心，江西南昌330013）

我国正大力发展高速铁路，大多采用高架桥形式。高速列车通过高架桥梁引起结构的振动问题成为研究热点，各国专家在理论和应用方面都做了大量工作。早期针对等截面均布梁提出的计算模型和计算方法主要是解析或半解析法［1-3］。后来随着计算机技术的发展，又提出了比较复杂的分析模型。其中一种是桥梁车辆耦合系统采取分离的方程，两者通过轮轨力平衡及几何相容条件联系，运用迭代法对车辆、轨道桥梁动力方程交叉求解，得到耦合系统的动态响应［4-10］。另一种是模型是建立车辆桥梁系统的耦合方程，桥梁结构采用有限元及模态分析法与子结构法模拟，车辆考虑为多自由度刚体，车桥耦合方程一般采用直接积分法求解［11-12］。前者时间步长的选取要求较高，后者则因车桥耦合系统的系数矩阵会随着车辆在桥上位置的变化而发生改变，这样在每一时间步求解时都必须重新产生和分解，而且随着车桥系统计算模型的复杂性增加，耦合的自由度数也将变大，使得计算量变大。

本文在华东交通大学雷晓燕教授［13］车辆-无砟轨道-桥梁四层梁模型的基础上，提出了新型轨道-桥梁单元和动轮单元，模型中只研究轮轨竖向动力响应；上部车辆系统和下部轨道系统沿线路方向左右对称，取结构的一半进行研究。整个系统分解为上部车辆和下部无砟轨道-桥梁两个子系统。模型中耦合系统的显式时变耦合运动方程，在每一步求解时，车辆和轨道系统之间的位移和力的协调关系自然得到满足，对时间步长的选取要求不高。同时模型针对系统中不同结构采用了不同自由度，因此该方法的计算精度高、程序编制容易，适合多节车辆通过时轨道结构的振动分析。

1 轨道-桥梁单元模型

本文模型针对桥上CRTS II型板式无砟轨道系统，将轨道-桥梁结构简化为四层梁单元模型，分别为钢轨、轨道板、底座混凝土支撑层和桥梁。ky1，cy1分别为轨下垫层支承弹性、阻尼系数；ky2，cy2分别为CA砂浆层的支承弹性、阻尼系数；ky3，cy3分别为混凝土垫层下桥梁的支承弹性、阻尼系数。

以多节点的一个广义梁单元对长度为L轨道-桥梁结构的四层梁模型进行离散，角标r，s，f ，b 分别表示钢轨、轨道板、底座混凝土板、桥梁，如图1所示。钢轨、轨道板、底座混凝土支撑层、桥梁的自由度数分别为Nr，Ns，Nf，Nb。轨道单元的总自由度为N，即N=Nr+Ns+Nf+Nb。桥梁轨道单元的节点位移向量为

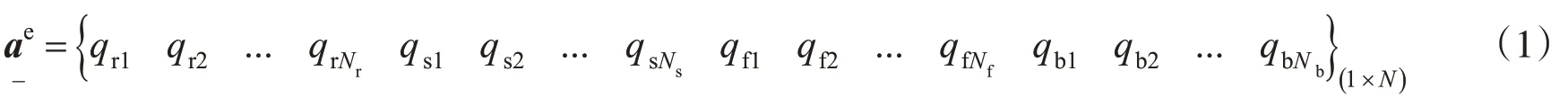
对应的轨道-桥梁单元的插值函数为

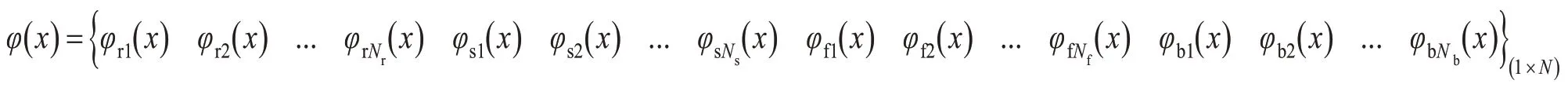
其中qrn(n=1，...，Nr)，qsn(n=1，...，Ns)，qnf(n=1，...，Nf)，qbn(n=1，...，Nb)分别为钢轨、轨道板、底座混凝土支撑层、桥梁的节点位移。

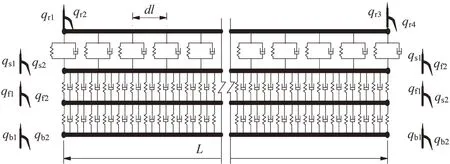
图1 CRTS II板式无砟轨道-桥梁结构单元模型Fig.1 CRTS II slab track-bridge element model

在文献【14】中，杨广军详细研究了在弹性支撑上的钢轨的多跨连续梁本征值问题，将钢轨模拟为弹性地基上的Euler 梁，研究表明其振型函数和相同结构简支梁的各阶振型函数完全相同。同时，将长厚比大于25的连续型轨道板、底座混凝土支撑层及桥梁模拟为梁模型，其模态函数可参考文献［15］。本文将钢轨部分的插值函数φrn(x)取为φr1(x)=1-，φr2(x)=x-，φr3(x)=，φr4(x)=-，φrn(x)=，(n=5，6，…，Νr)。同时，将钢轨部分插值函数表达式中的角标r替换为s，f ，b，即分别为轨道板、底座混凝土板、桥梁的对应的插值函数，由于轨道板、底座混凝土板、桥梁的振动频率相对于钢轨要低，尤其是桥梁，可以采用相对较少的自由度即可获得满意的精度，因此单元中轨道板、底座混凝土支撑层、桥梁采用不同的自由度数。

上述有关轨道-桥梁单元建模的方法，融合和有限元法与模态分析法的特点。这种方法与一般的常规的轨道-桥梁广义梁单元相比，减少了计算自由度，且只有一个大单元，不需要判断车辆所在轨道-桥梁系统的具体单元位置，因此具有自由度少、不需要组合轨道-桥梁单元有限元总矩阵、编程简单的特点。

根据有限元法推导单元的刚度矩阵、质量矩阵和阻尼矩阵。

下部四层轨道-桥梁单元的质量矩阵：

四层轨道-桥梁单元的刚度矩阵：

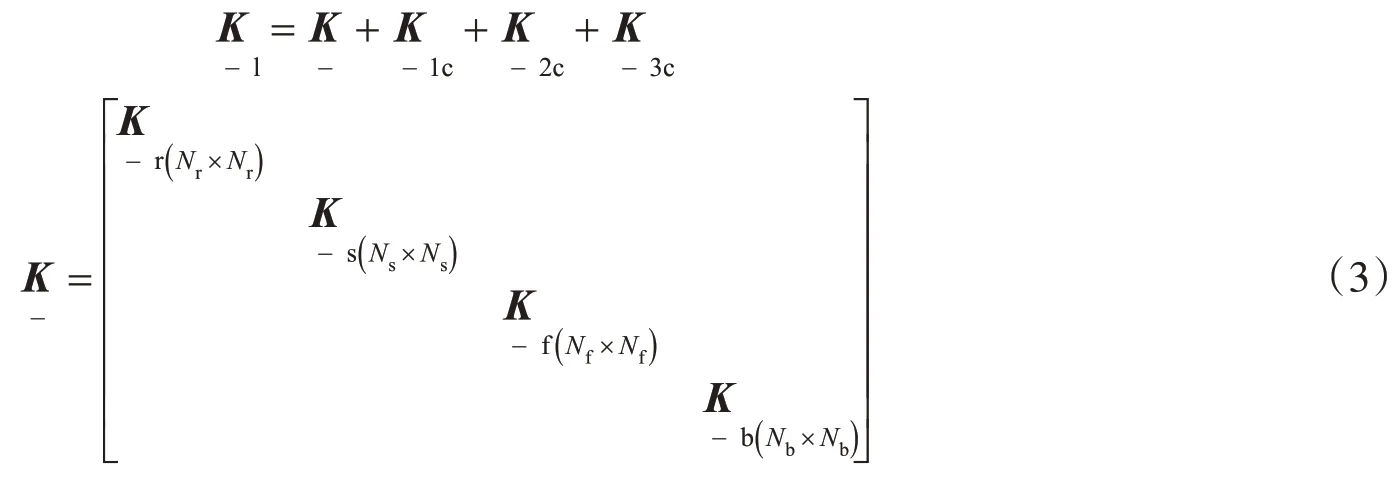
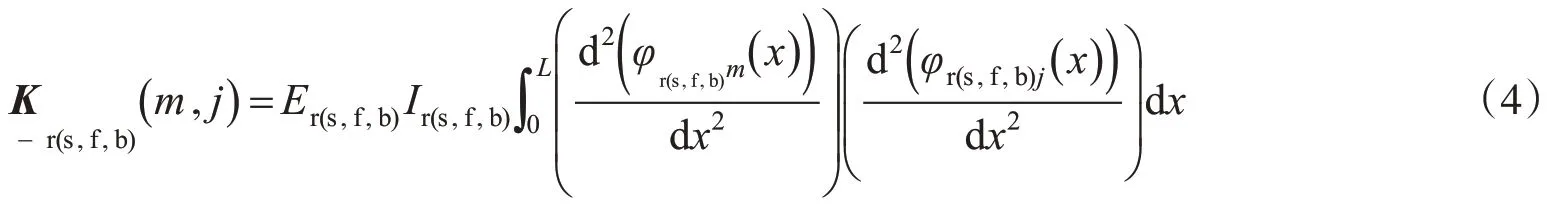
设整个单元长度L中共有t个等距的离散支承，每两个支撑间的间距为dl。假设第一个支撑在单元的原点处，第i个支撑位置的坐标为xsi。且xsi=(i-1)dl，其中i=1，2，…，s。

则第i个支撑位置处的弹簧位移为

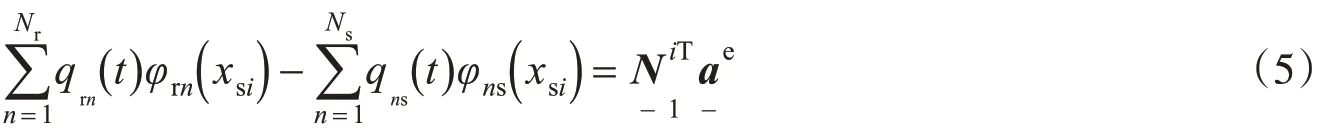
第一层连续支承弹簧的位移为

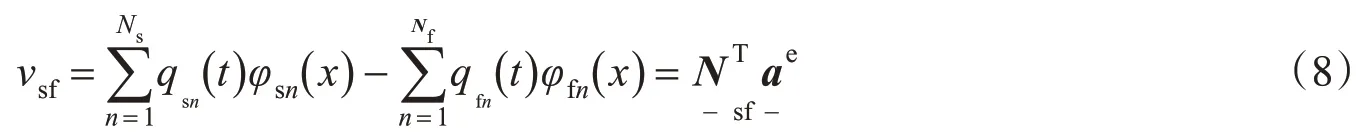
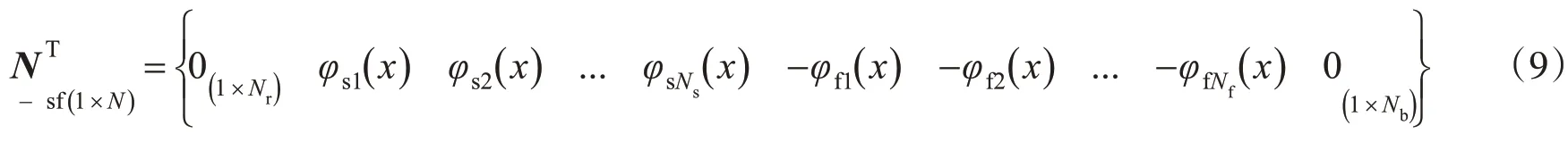
四层轨道-桥梁单元的阻尼矩阵

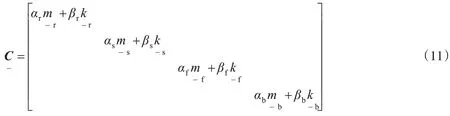
其中αr，s，f，b，βr，s，f，b分别为钢轨、轨道板、底座混凝土板、桥梁的比例阻尼系数。

2 车辆单元模型

将每节车辆离散为4个具有二系悬挂的独立动轮单元，车体、转向架和车轮均为刚体，只考虑其沉浮振动；轮轨间为弹性接触；车轮始终与钢轨接触，即车轮不悬空。

车辆单元模型见图2，Mc，Mt为车体和转向架的质量；Ks1，Cs1分别为车辆一、二系悬挂刚度、阻尼系数；Ks2，Cs2为车辆二系悬挂刚度、阻尼系数；Mwi(i=1，2，3，4)为第i个车轮质量。η表示轨面随机不平顺幅值，与第i车轮接触处不平顺幅值为ηi(i=1，2，3，4)。

考虑钢轨有Νr个自由度，每个单轮有3 个自由度，即车辆单元的自由度有(Νr+12 )个。模型有(Νr+12) 个节点，分别为r1，r2，…，rΝr，c1，t1，w1，c2，t2，w2，…，c4，t4，w4；节点位移向量为

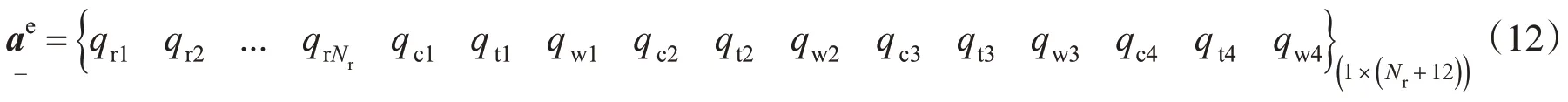
Qi为第i轮与钢轨的接触点，设原点与Qi间的距离为xi，xi=vt+ai，即t时刻第i个车轮与原点的距离，ai为第i车轮在初始时刻与原点的距离。下部梁长为L。

假定下部梁单元（钢轨）的位移模式为

其中φrn(x)为梁的插值函数，其形式与轨道-桥梁单元的钢轨的差值函数一致。qrn(t)为n节点的节点位移。根据有限元法推导单元的质量、刚度及阻尼矩阵。

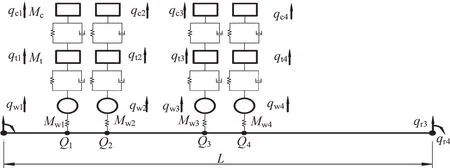
图2 车辆单元模型Fig.2 Vehicle element model

车辆单元的质量矩阵：

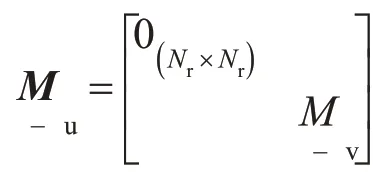
其中

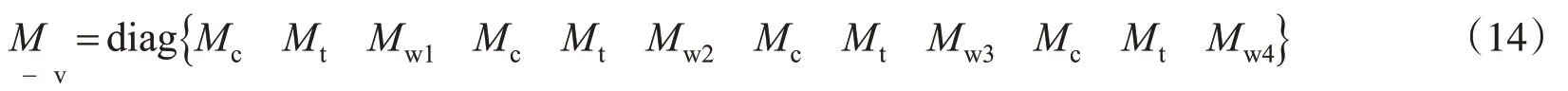
上部车辆单元的刚度矩阵：

其中

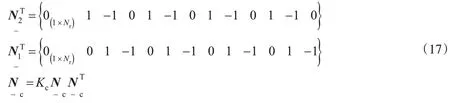
车辆单元的阻尼矩阵：

3 列车-轨道-桥梁耦合系统动力方程

整个离散成车辆和轨道-桥梁单元，一节车辆离散为4个动轮单元。程序编制时由于轨道-桥梁单元是离散成一个多自由度的单元，单元矩阵即是总矩阵，所以不需要进行总矩阵的组合，且不需要判断车辆所在轨道-桥梁系统的具体单元位置，因此程序编制容易。同时只需形成一次轨道-桥梁系统的特性矩阵，在以后每一时步的计算中，再组集车辆单元的刚度、质量和阻尼矩阵，而且单元中针对振动频率不同的部分选取了不同的自由度，大大降低了系统的自由度数，所以计算效率大大地提高了。

4 算例

计算时选取两节车辆，分析轨道-桥梁结构的动力特性。车辆为和谐号CRH3，车速为83 m·s-1，基本参数见表1。轨道条件单跨为32 m的双线简支箱形梁桥，轨道板为连续轨道板，其参数取自文献［16］，具体参数见表2。线路总长160 m，轨道-桥梁单元中钢轨、轨道板、底座混凝土板和桥梁分别取200，150，150，40 个自由度［13］。Newmark数值积分法时间步长为0.001 s，考虑轨道随机不平顺状态时，采用最接近我国高速铁路状况的德国低干扰谱，采用三角函数法［4］进行数值模拟，代入式（20）可得到其引起的附加动荷载。计算结果见图3～图7。

表1 和谐号高速动车CRH3车辆结构参数Tab.1 CRH3 vehicle parameters

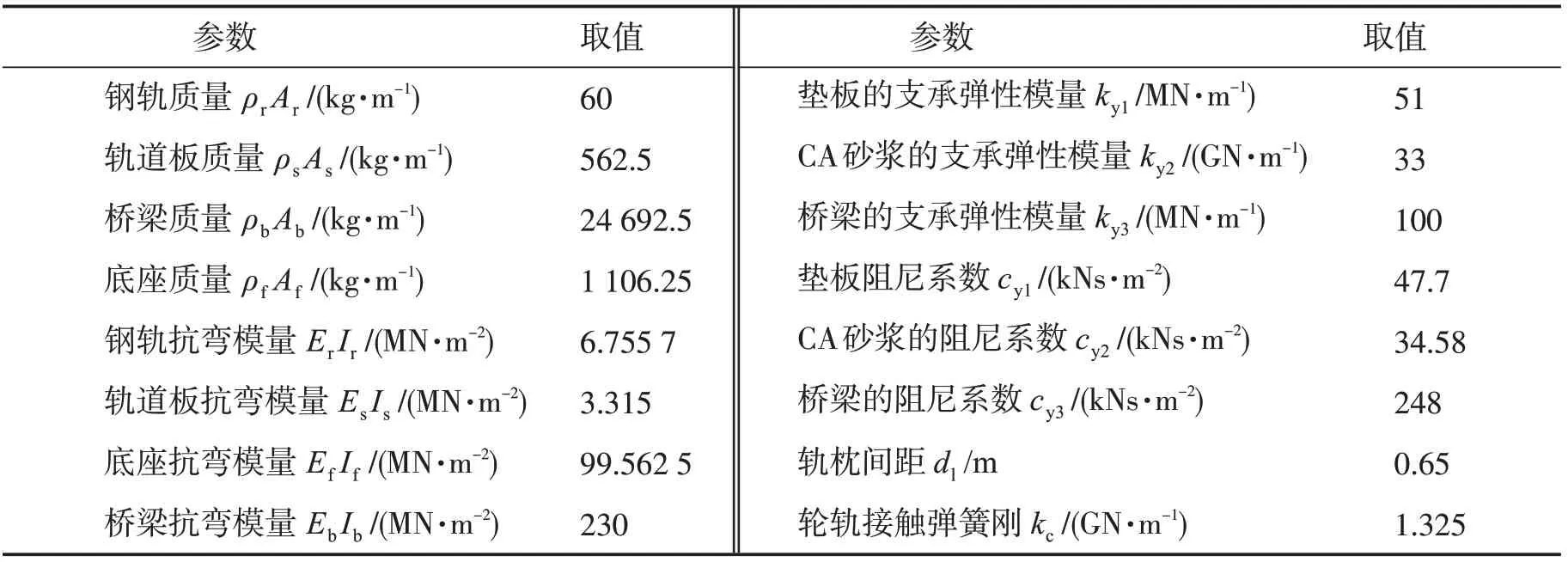
表2 CRTSⅡ型板式无砟轨道桥梁结构参数Tab.2 CRTSⅡunballast slab track and bridge parameters

图3～图7是部分具有代表性的轨道系统竖向动力时程曲线，其中包括：竖向轮轨作用力，钢轨、桥梁竖向位移曲线、钢轨、桥梁竖向加速度曲线。从图3～图7可以看出，各指标数值均在通常范围内，各曲线趋势符合物理概念。在钢轨竖向位移曲线中可以看出，当车轮经过钢轨某一处时，位移数值均较大，反之，位移数值均很小，甚至接近零；此外，还可从图中的尖点来确定车轮的数目，车辆何时通过钢轨观察点，以及两尖点间的时间差来确定车型，这些都说明本文模型得正确可行，也能较好地反映无砟轨道桥梁结构的竖向动力特性。

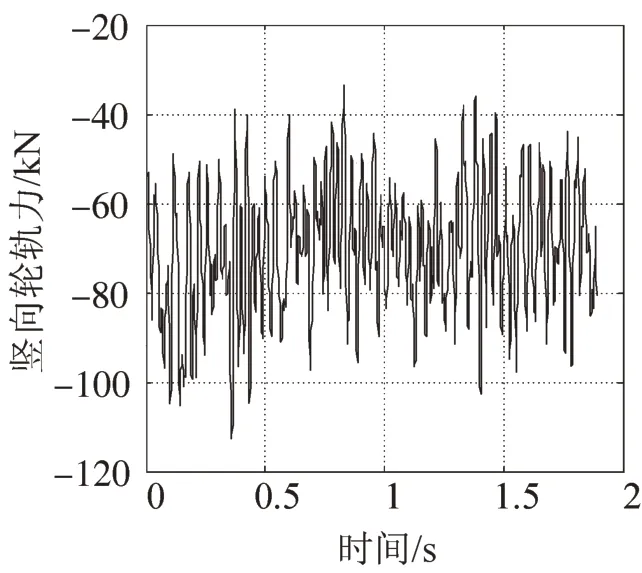
图3 竖向轮轨作用力Fig.3 Vertical wheel/rail contact force

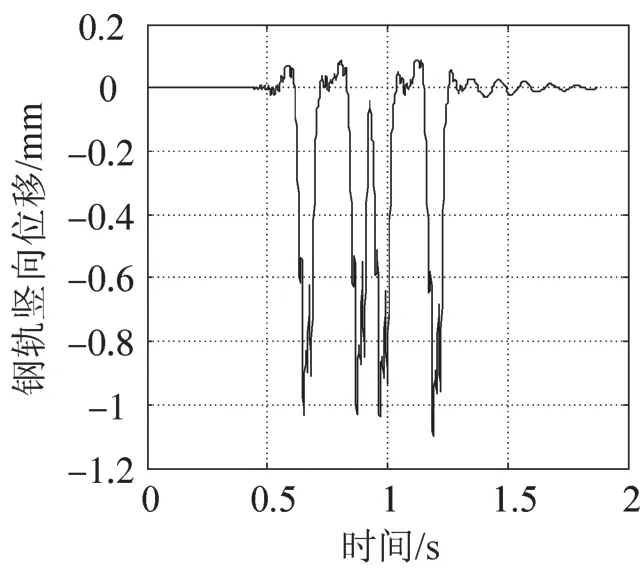
图4 钢轨竖向位移fig.4 Vertical displacement of rail

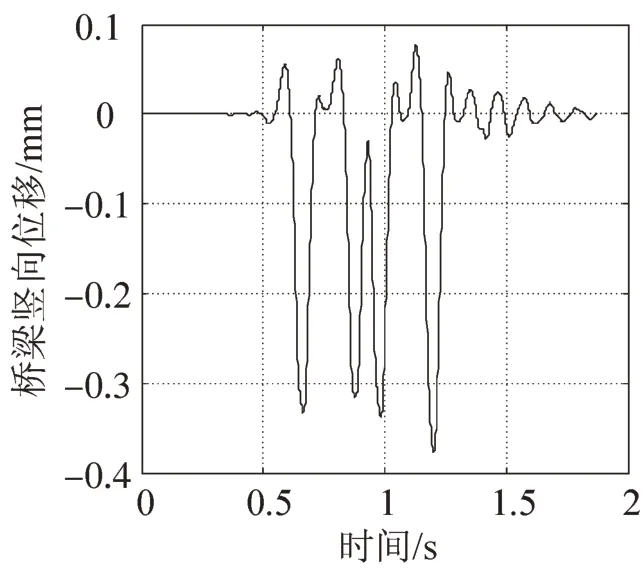
图5 桥梁竖向位移Fig.5 Vertical displacement of bridge

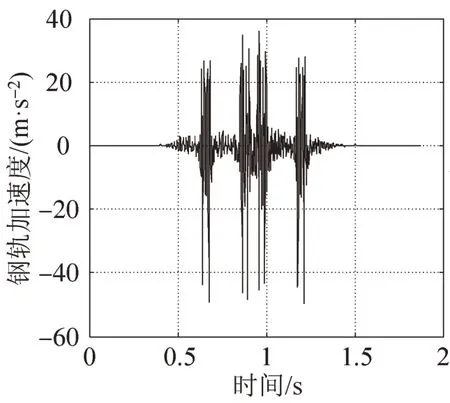
图6 钢轨竖向加速度Fig.6 Vertical acceleration of rail

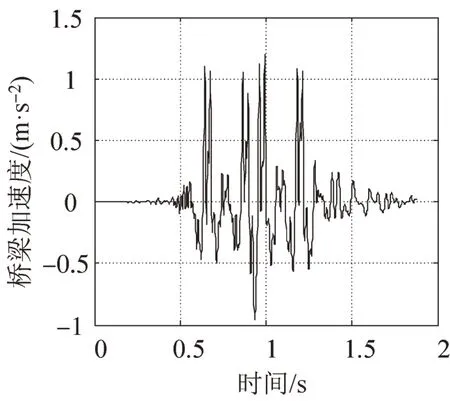
图7 桥梁竖向加速度Fig.7 Vertical acceleration of bridge

5 结论

提出的新型FEM梁单元的插值函数与简支梁振动精确模态函数一致，因此该梁单元所求解可以看成是该梁振动的精确解，这样的梁单元是以梁振动精确模态函数为插值函数的特殊单元，可以较少的自由度获得较高的精度。此类单元结合了有限元法与模态分析法的优点，适合分析其振动模态已知，形状规则的振动结构。同时基于能量原理建立了动力控制方程，使得单元质量、刚度、阻尼矩阵形式对称，而且无砟轨道-桥梁单元是离散成一个多自由度的单元，单元矩阵即是总矩阵，所以不需要进行总矩阵的组合，且不需要判断车辆所在无砟轨道-桥梁系统的具体单元位置，这样就降低了程序编制的难度。同时单元中针对振动频率不同的部分选取了不同的自由度，大大降低了系统的自由度数，又由于整个列车-轨道-桥梁系统只包含车辆单元和轨道-桥梁两种单元，且每个时间步长中无砟轨道-桥梁单元对应的质量、刚度、阻尼矩阵表达式不变，因而提高了计算效率。

文中运用模型计算了具有随机不平顺的无砟轨道桥梁时变系统竖向振动响应，得出了系统响应典型时程曲线。其计算数值及曲线波形，都可以较好地反映无砟轨道桥梁系统的振动特性。

［1］TIMOSHENKO.工程中的振动问题［M］.胡人礼，译.北京：人民铁道出版社，1978：35-48.

［2］WEN R K.Dynamic response of beams traversed by two-axel loads［J］.Journal of Engineering Mechanics Division，ASCE，1960，86：32-38.

［3］JACOBSEN L S.Engineering vibrations［M］.New York：McGraw Hill，1958：49-58.

［4］雷晓燕.轨道力学与工程新方法［M］.北京：中国铁道出版社，2002：12-37.

［5］曹雪芹，刘必胜，吴鹏贤.桥梁结构动力分析［M］.北京：中国铁道出版社，1987：75-89.

［6］李小珍.高速铁路列车-桥梁系统耦合振动理论及应用研究［D］.成都：西南交通大学，2000：46-70.

［7］沈锐利.高速铁路线上简支梁桥与车辆耦合振动研究［D］.成都：西南交通大学，1998：71-98.

［8］翟婉明.车辆-轨道耦合动力学［M］.3版.北京：科学出版社，2007：11-73.

［9］CHU K H.Dynamic interaction of railway train and bridge［J］.Vehicle System Dynamics，1980，9（4）：207-236.

［10］蔡成标，翟婉明，王开云.高速列车与桥上板式轨道动力录仿真分析［J］.中国铁道科学，2004，25（5）：57-60.

［11］娄平，曾庆元.车辆-轨道-桥梁系统竖向运动方程的建立［J］.铁道学报，2005，26（5）：17-27.