指针式仪表图像高斯同态滤波增强算法研究

2013-12-20郭清宇彭芳芳

中原工学院学报 2013年5期

郭清宇，彭芳芳

（中原工学院，郑州450007）

目前，在工业中机器视觉技术应用比较广泛，其中近80%的机器视觉系统主要应用在检测方面.仪表识别是机器视觉技术中非常重要的一项内容，尚处于研究阶段.仪表分为数字式仪表和指针式仪表，指针式仪表广泛应用于工业生产中.指针式仪表得到的信号不是数字信号，不能被直接采集到计算机系统，且读数一般由人工完成，存在读数误差大、工作强度大、效率低、可靠性差等问题［1］.

指针式仪表识别的关键是图像的预处理，预处理的好坏影响整个仪表系统的性能［2］.在图像采集过程中，因光照不佳会使图像产生反光、眩光，采集到的图像亮度也不均匀，局部信息难以辨认.要使指针式仪表图像达到自动识别的要求，必须进行图像增强处理.图像对比度增强的方法有很多，包括图像灰度变换、图像直方图处理、同态滤波算法增强、基于梯度场放大、基于Retinex算法增强等.本文利用同态滤波算法增强图像，可得到视觉效果较好的仪表图像［3］.

1 指针式仪表图像预处理

图像预处理包括图像滤波、图像的二值化、图像的平滑等.预处理图片的质量直接影响后续识别结果的正确性.

指针式仪表图像预处理包括3个方面：图像分割、图像质量改善、图像二值化.图像分割是便于图像后续处理；改善图像质量包括去噪声和图像增强，现有的图像增强方法包括图像结构增强、对比度增强等；图像二值化是使指针式仪表图像特征区域的特点更加突出.图像对比度增强的方法主要有3类：第一类是使用空间域的方法，如直方图均衡化、梯度场增强、灰度拉伸等；第二类是使用频率域的方法，该类方法把图像作为波信号，利用信号处理方法对图像波信号进行处理，如傅里叶变换、同态滤波、小波变换等；第三类是模糊增强方法，常用的基于粗糙集理论的方法是将图像分为目标区域和背景区域，再使用不同的函数来增强.本文利用高斯同态滤波算法增强指针式仪表图像的对比度，可得到视觉效果较好的仪表图像［3—4］.

2 指针式仪表图像增强方法

由于待处理的指针式仪表图像可能存在光照不均匀和噪声干扰，直接处理采集到的图像会影响到识别，因此，对于光照不均匀的图像，可以采取同态滤波增强算法来处理，以改善图像质量，提高识别的精度.

2.1 同态滤波算法原理

同态滤波算法是把频率过滤和灰度变换结合起来的一种图像处理方法，依靠图像的照明－反射模型作为频域处理的基础，通过压缩亮度范围和增强对比度来改善图像的质量.这种方法符合人眼对于图像亮度的视觉特性，避免了直接对图像进行傅立叶变换处理产生的失真.对图像做非线性变换以后，图像的非可加性因素变成可加性因素，容易进行滤波处理［5］.

同态滤波算法的基本原理是：将像元灰度值看作是照度和反射两个组分的产物.由于照度相对变化很小，可以看作是图像的低频成分，而反射则是高频成分.通过分别处理照度和反射对像元灰度值的影响，达到揭示阴影区细节特征的目的.

在照度和反射模型中，图像可表示为：

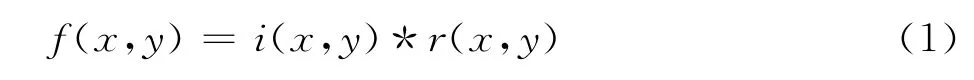
其中，照度分量i（x，y）集中在低频段，反射分量r（x，y）集中在高频段.同态滤波法通过滤波函数估算图像的低频成分和高频成分，滤去低频成分，增强图像对比度，过程如图1所示［5］.

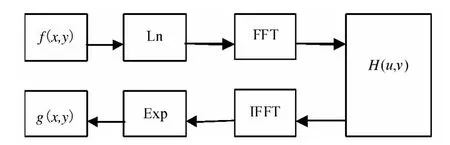
图1 同态滤波过程框图

H（u，v）是高通滤波函数.选择合适的 H（u，v）对同态滤波算法的效果有关键影响.

2.2 高斯同态滤波对仪表图像的增强作用

同态滤波是图像预处理中的一种常用算法.直接利用同态滤波算法对指针式仪表图像预处理的结果不是很理想，影响滤波后的二值化效果.本文采用基于高斯滤波函数改进的同态滤波算法对指针式仪表图像进行预处理，具体方法如下.

在对图像进行FFT变换前，对式（1）两端取对数，把照明分量和反射分量分离，得到：

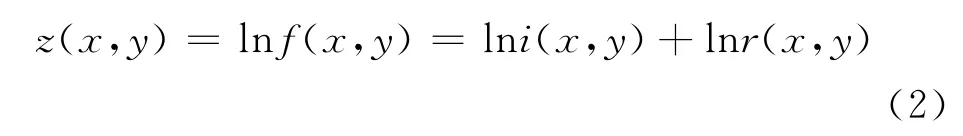
在分离出高、低频分量后，通过FFT变换，可将式（2）用下式表示：

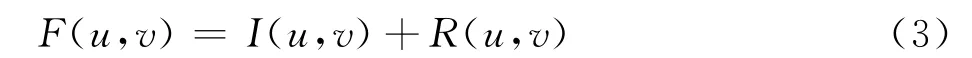
即

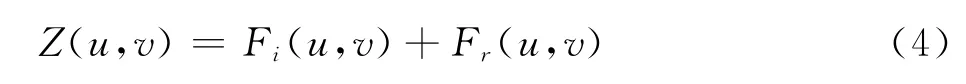
为了降低低频成分，使用高通滤波函数H（u，v）对其进行滤波.高通滤波器的传递函数形式为：

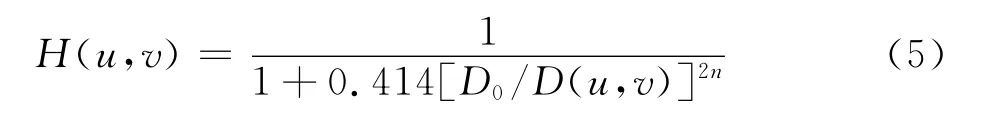
以Rh表示高频增益，Rl表示低频增益，D（u，v）表示频率（u，v）距滤波器中心（u0，v0）的距离，传统的同态滤波函数如图2所示［6］.

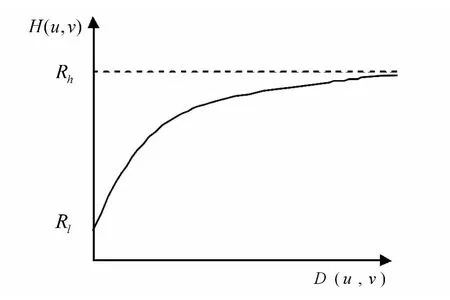
图2 传统的同态滤波函数

当Rh＞1且Rl＜1时，此滤波函数可以同时抑制照明分量，增强反射分量，满足动态范围的压缩和对比度的增强.根据处理目的不同，选择不同的滤波函数.高斯高通滤波器是频域内经常用到的高通滤波器.滤波函数为：

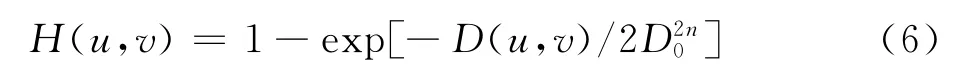
利用式（6）可以构造一个高通滤波器.下面对上述高通滤波器稍加修改，得到如下高斯高通滤波函数：

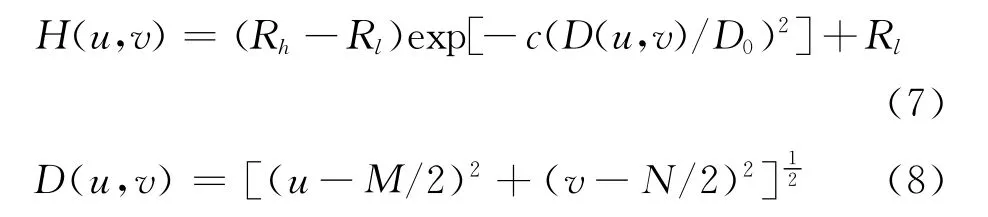
式中：D0是u0和v0为0时的D（u，v）值，表示截止频率，可以根据需要设定，以达到最佳效果，如图3所示.

图3 同态滤波传递函数图

根据原始指针式仪表的图像特征，经过实验，得到同态滤波后的结果：

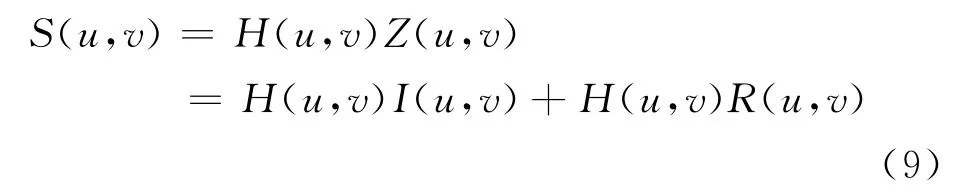
最后，对滤波后的图像进行IFFT变换，得到空域输出，如下式所示：

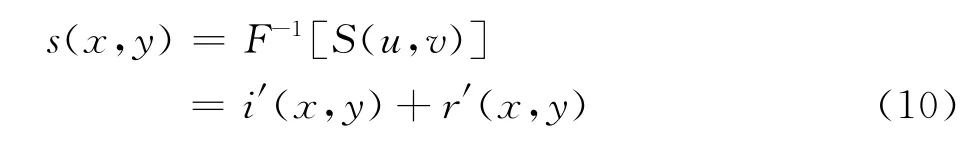
由于采用取对数的方法将照度分量和反射分量分开，因此要对s（x，y）进行反对数运算，如式（11）所示：

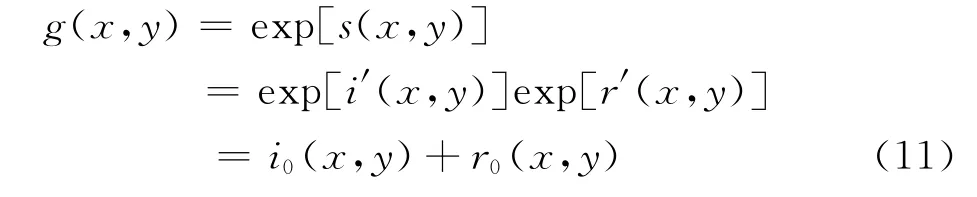
2.3 参数选取

截止频率D0与照度分量和反射分量有关，选择比较困难，需要通过反复实践确定合适的值.本文通过对照度场的频谱进行分析，得到光照特性，进而选取同态滤波器参数.在频域中，图像的空间信息表现为不同频率分量的组合.对于一个尺寸为M×N的图像的函数f（x，y），它的离散傅里叶变换如下式所示：

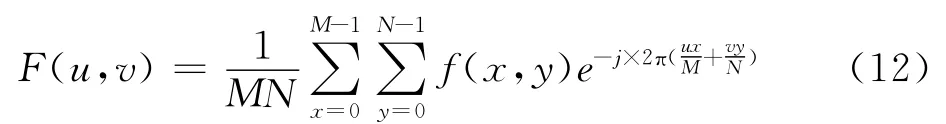
式中：u＝0，1，2…，M－1；v＝0，1，…，N－1.频谱可表示成：

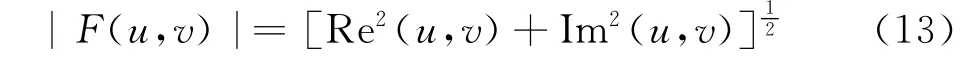
式中：Re（u，v）和Im（u，v）分别是F（u，v）的实部和虚部.

如果光照是均匀的，则光照场的频谱只有直流分量；当光照不均匀时，随着光照不均匀程度的增加，谐波分量所占的比例就会增加.在不均匀光照条件下，计算第n次谐波分量占谐波总量的比例，可以得到占比较大的谐波频率的范围，对应的频率即为截止频率.

由式（13）计算不同D（u，v）对应的频率谱，它们位于以原点为中心、D（u，v）为半径的圆周上.然后再计算图像功率P（u，v）占总图像功率Pl的比例α：

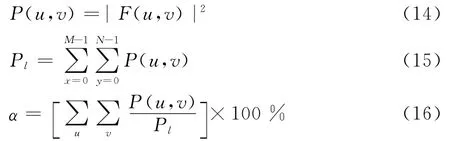
把α从大到小排序，计算前n项的和S，到S＞0.7时停止运算，得到对应的D0值.

3 图像二值化

3.1 图像二值化原理

图像二值化处理就是将图像上点的灰度值设置为0或255，即通过选取适当的阈值将256个亮度等级的灰度图像转化为可以反映图像整体和局部特征的二值化图像，使图像呈现出明显的黑白效果.

二值化的基本过程如下：进行图像预处理，降低或去除噪声，用相关算法确定最佳阈值T.凡是像素的灰度值大于等于这个阈值的，设为255，小于这个阈值的，设为0.这样，处理后的图像就只有黑、白两色，从而将灰度范围划分成目标和背景两类，实现图像的二值化.其原理如式（17）所示：

图像二值化的方法有很多，主要的有以下3种：全局阈值二值化、局部阈值二值化、多阈值二值化.阈值选取也有很多方法，其中运用最广泛的是最大类间方差法［3—4］.

3.2 最大类间方差法二值化

最大类间方差法是由日本学者大津（Nobuyuki Otsu）于1979年提出的，是一种自适应的阈值确定方法，又叫大津法，简称OTSU.它基于整幅图像的统计特性实现阈值的自动选取，是二值化中最优秀的算法.它按图像的灰度特性，将图像分成背景和目标两部分.背景和目标之间的类间方差越大，说明构成图像的两部分的差别越大，当部分目标错分为背景或部分背景错分为目标时，都会导致两部分差别变小.因此，类间方差最大的分割意味着错分概率最小.

OTSU算法的基本思想是用一个假定的灰度值T把图像的灰度分为两组，如果两组的类间方差达到最大时，则此灰度值T就是图像二值化的最佳阈值［4］.

4 算法仿真实现

根据上面的分析，用Matlab 7.0进行编程仿真，可实现本文的算法.具体仿真步骤如下：

（1）读入原始图像I；

（2）将原始图像转换成二维的灰度图像，并取I＝double（rgb2gray（I））；

（3）生成频率序列矩阵，［M，N］＝size（I）；

（4）设置截止频率D0等参数；

（5）对I进行对数变换，取I1＝log（I＋1）；

（6）对I1进行快速傅里叶变换，得到FI＝fft2（I1）；

（7）构造高通滤波函数 H（u，v）；

（8）利用步骤（7）得到的滤波函数进行滤波，接着进行傅立叶逆变换，I2＝ifft2（H.＊FI）；

（9）对步骤（8）得到的结果进行指数运算，I3＝real（exp（I2））；

（10）输出最后的结果I3.

在实验中用到的参数有：Rl＝0.1，Rh＝4，c＝2，D0＝10.3.

实验表明，通过对原始图像进行上述处理，图像的质量得到明显改善.在仪表图像增强之后，再对其进行最大类间方差二值化，以验证增强的效果.采用不同算法的效果对比图如图4所示.

通过分析图4可以看出，原始图像（图4（a））存在光照不均匀的现象，图像上半部分比较暗，下半部分比较亮，表盘也存在噪声干扰.对原图像进行最大类间方差二值化（图4（b）），可以明显看到，二值图周围有大量的干扰信息，暗区的数字信息被干扰，表盘也存在噪声干扰.为了增强图像的对比度，把有效信息和干扰信息分离，在同态滤波的基础上对图像进行预处理.图4（c）为一般同态滤波增强后的图像，从图中可以看出，表盘的有效信息清晰度虽然得到明显的改善，但是依然有干扰信息.从对其二值化后的效果图（图4（e））可以看出，用这种方法去除噪声的效果并不理想，表盘中间仍有很多干扰信息，指针清晰度也不是很高，存在不同程度的断续，影响后续图像的识别.从利用高斯同态滤波增强算法得到的效果图（图4（d））可以看出，刻度线以及刻度数字完整无缺，表盘干净，没有干扰信息，原图像中偏暗的部分也得到了增强.虽然周围还有一小部分干扰信息，但是不影响有效信息的分割，在后续处理过程中采用有关图像分割技术可以很容易处理掉.仿真结果说明，以上图像增强方法对光照不均匀的仪表图像有比较好的增强效果.