空间不均匀的Boltzmann方程的稳定性

晋守博,张 磊

1.宿州学院数学与统计学院,安徽宿州，234000 2.宿州市第二中学，安徽宿州，234000

最近,关于Boltzmann方程稳定性的研究已经越来越引起人们的重视,该方程描述了经典粒子系统的变化规律,在流体力学中具有重要作用，在空间不均匀的情况下,Boltzmann方程具有下面形式:

(1)

方程的初始条件为：

f(0,x,v)=f0(x,v)

(2)

方程中的f(t,x,v)表示在t时刻点x处速度为v的粒子的密度分布函数，碰撞算子J(f,f)(t,x,v)描述了粒子双边碰撞的情况，可以表示为：

J(f,f)(t,x,v)=Q+(f,f)-fR(f)

(3)

其中

(4)

和

(5)

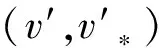
=v*-(v-v*,w)w

(6)

当0<δ≤1时，称方程(1)为具有硬位势的Boltzmann方程，当δ=0时，称方程(1)为具有Maxwell形式的Boltzmann方程，当-2<δ<0时，称方程(1)为具有软位势的Boltzmann方程，文[1]讨论了具有弹性碰撞的Boltzmann方程的L1稳定性；当δ=0时，文[2]和[3]分析了具有非弹性碰撞的Boltzmann方程在特殊范数下的稳定性，文[4]讨论了一类耗散线性Boltzmann方程的解的正则性。本文将利用文献[5]的方法考查0<δ≤1的情况，需要指出的是文中不同公式中的C代表不同的常数。为了计算方便，首先引入下面记号。

f#(t,x,v)=f(t,x+vt,v)

n(v,v*)=(v-v*)/|v-v*|

S(f,g)(t,x,v)=[Q(f,g)+fR(g)+Q(g,f)+gR(f)](t,x,v)

首先给出下面引理：

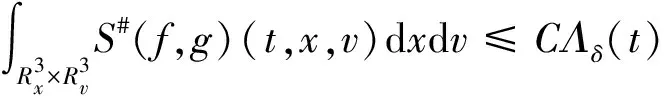
引理2对任意p>0，当-3<δ≤0时，必存在常数C>0使得：

(7)

证明:对任意p>0，有

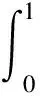
利用已知条件可得：

引理3当0<δ≤1时，如果f#(t,x,v)≤δ0e-p|x|2e-q|v|2，则存在0<η≪min{p,q}，使得：

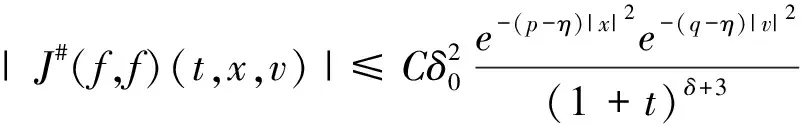
证明:先对碰撞算子的正向部分进行估计。

当t≤1时，由于

≤C(1+|v|δ)

所以再利用1+|v|δ≤eη|v|2可得：

当t>1时，令x+t(v-v*)=s可得：

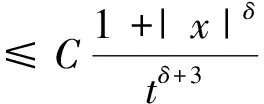
故将两者结合可得，对任意t>0有：

同理可对负项部分进行类似估计，最后将两者结合可以得到:

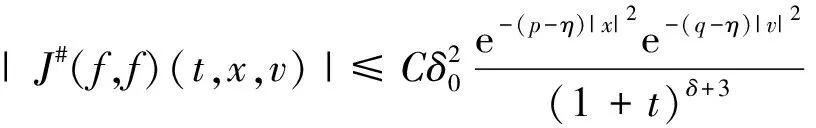
下面给出本文的主要定理。

定理1设f(t,x,v)和g(t,x,v)为方程(1)的两个经典解，其初值分别为f(0,x,v)=f0(x,v)和g(0,x,v)=g0(x,v)，如果对任意t≥0，f和g满足：

f#(t,x,v)≤δ0e-p|x|2e-q|v|2

g#(t,x,v)≤δ0e-p|x|2e-q|v|2(0<δ0≪1)

其中p,q>0，则当0<δ0≤1时，必存在常数C>0，使得：

(8)

证明：记H(t)=L(t)+KDδ(t)(K>0为待定常数)，利用引理1可得：

(9)

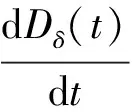
∂t[f(t,x+vt+τn,v*)]

=(∂tf+v*·xf)(t,x+vt+τn,v*)

+(v-v*)·xf(t,x+vt+τn,v*)

=J(f,f)(t,x+vt+τn,v*)

+∂τ[|v-v*|f(t,x+vt+τn,v*)]

经过计算可得:

∂t[|f-g|#(t,x,v)(f+g)(t,x+vt+τn,v*)]

=∂t|f-g|#(t,x,v)(f+g)(t,x+vt+τn,v*)

+|f-g|#(t,x,v)∂τ(f+g)(t,x+vt+τn,v*)

≤S#(|f-g|,f+g)(t,x,v)(f+g)(t,x+vt+τn,v*)+|f-g|#(t,x,v)(S(f,f)+S(g,g))(t,x+vt+τn,v*)+∂τ[|v-v*||f-g|#(t,x,v)(f+g)(t,x+vt+τn,v*)]

其中：

和

利用已知条件对J1和J2进行估计，利用引理1和引理2可得：

利用引理2和引理3可得：

+vt+τn,v*)dv*dτ

从而利用公式(9)可得:

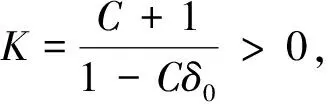
利用Gronwall不等式可知:

由H(t)的定义可以得到：

‖f(t)-g(t)‖L1≤H(t)≤C‖f(t)-g(t)‖L1

故

‖f(t)-g(t)‖L1≤H(t)≤CH(0)≤C‖f(0)-g(0)‖L1。

参考文献：

[1]Wu Zhigang.L1 and BV-type stability of the inelastic Boltzmann equation near vacuum[J].Continuum Mach Thermodyn，2010,22(3):239-249

[2]Jin Shoubo，Chen Panfeng.Stability of Dissipative Boltzmann equation for one dimensional granular gases[J].Annals of Differential Equation，2011,27(2):145-149

[3]晋守博，肖志涛，张光辉.广义Kac方程的解的渐近稳定性[J].大学数学，2010,26(4):21-25

[4]晋守博，陈攀峰，孙善辉.耗散线性Boltzmann方程的解的正则性[J].数学物理学报，2011,31A(6):1662-1668

[5]Duan Renjun，Yang Tong，Zhu Changjiang，L1 and BV-type stability of Boltzmann equation with external forces[J].Journal of Differential Equations，2006,227(1):1-28