一种基于置信规则的模糊推理算法

陈 晨，周 勇

(南京航空航天大学计算机科学与技术学院，江苏南京 210016)

由于在决策过程中具有不可替代的作用，因此在工程实际中，综合使用定量信息和专家提供的不完整的或不精确的主观信息，对决策问题进行分析至关重要。领域专家提供的评价等级可能具有两种不确定性:概率不确定性和模糊不确定性，对于同时具有随机性和模糊性问题，传统的决策方法往往只能解决某一种不确定性。基于概率理论的Bayes方法［1］偏重于处理定量信息，只能处理概率不确定性;基于传统的DS理论［2］能够有效利用定量信息和定性知识，但也只能处理概率不确定性;基于模糊IF－THEN规则的方法［3］能够有效利用定量信息和定性知识，可以处理模糊不确定性，但无法较好地处理概率不确定性。

作为使用模糊专家系统进行决策和分析的关键环节，模糊推理方法的研究更是备受关注。在模糊专家系统中，常用的模糊推理方法有基于模糊关系的合成推理方法(CRI)［4］，是基于模糊 IF－THEN规则的;基于相似性的推理方法［5］，是基于加权模糊规则的。由于规则本身的表达能力限制，偏重于描述知识的模糊性，因此模糊推理过程只注重模糊性，忽略了随机性。Yang等为了使规则能够包含更多的信息、更加接近实际表达方式，对传统模糊IF－TEHN规则进行改进，提出了置信规则库［6－7］的概念，加入了前提属性权重和规则权重的描述，规则的结论部分加入置信度，采用分布式方式表达，在增加了规则包含的信息量的同时，将概率不确定性与模糊不确定性统一于规则描述中，但目前还没有一种可行的模糊推理方法，能够在置信规则的基础上实现推理过程。为有效利用各种不确定性的定量信息和定性知识，实现复杂问题决策，本文提出一种基于置信规则的模糊推理算法，该算法是基于置信规则的，将单个前件匹配度依据其相对重要程度加权求和，把前提属性权重和规则权重融入推理过程，支持规则前件取值于连续的论域，置信规则的分布式结论则采用模糊集加权计算，结合Mamdani算法［8］推理给出最终的推理结果。文中给出了详细的推理步骤和直观的图形解释，并把基于置信规则的知识表达方式和新的推理算法引入到FuzzyCLIPS工具语言中，将扩展后的FuzzyCLIPS应用于鱼雷规避系统仿真，得到了较优的规避方案。

1 置信规则中前提与结论的计算

1.1 置信规则库理论简介

在IF－THEN规则的结果部分加入置信度，并同时考虑前提属性权重和规则权重，就得到置信规则。把一系列置信规则集合到一起便构成了置信规则库。其中第k条置信规则的描述表示如下

并有规则权重 θk和属性权重 δ1，k，δ2，k，…，δMk，k。其中，θk表示第k条规则的规则权重，它反映了第k条规则相对于其它置信规则的重要程度;δi，k表示在第k条规则中第i个前提属性的权重，反映了在规则中第i个前提属性的相对重要性;βj，k表示在第k条规则中第j个评价结果Dj的相对置信度。这里可以假设L条规则是相互独立的，亦即参考值集合A1，A2，…，AL是相互独立的。

1.2 基于相对重要程度的整体前件匹配度

Mamdani模糊推理算法中没有考虑前提属性对结论贡献的不同，认为所有前提属性对结论的贡献相同;在推理过程中只注重知识的模糊性方面，忽略了事件发生的随机性。基于相对重要程度的前件计算方法，支持各种输入形式，例如输入(高，0.9)表示取“高”的可能性是90%，既考虑了定性概念的模糊性又注重了发生的随机性。先计算单个前件的匹配度ωAi，再根据前提属性权重的不同，对单个前件的匹配度进行加权求和，得到整体前件匹配度。

输入x1，x2，…，xMk既可以是定性知识，也可以是定量信息。当输入(x1，γ1)(x2，γ2)…(xmk，γmk)，γi表示事件发生的概率。运用Mamdani模糊推理算法进行推理

基于“相对重要程度”的整体前件匹配度的计算方法，将ωi×γi作为输入事实对于单个前件的匹配程度，表示Aki*对Aki的匹配度，根据规则中前提属性权重的不同，为每个前件指定一个“相对重要程度”i=1，2，…，n，并以此为权值，对单个前件的匹配度加权求和，得到整体前件匹配度s。

1.3 置信规则的结论计算

置信规则的评价结果是分布式的，赋予每个部分评价一个权重，表示这个结论相对于规则的置信度。Mamdani模糊推理算法使用的规则结论是单一的，使用该算法处理分布式结论时，要对分布式结论拆分，将结论的置信度作为整条规则权重的一部分，但增大了规则库的规模，丢失了分布式评价权重的意义。加权复合结论，以置信规则结论各项置信度作为权重，将相应模糊子集加权合并，把合并后的复合结论作为规则结论。

其中scaleTo(D，n)将模糊集D缩放为原先的n倍。

以置信规则R0为例，说明计算复合结论的计算方法

将结论以模糊集形式表示，转化后的规则为:

D*=scaleTo(N，0.6)∪scaleTo(O，0.3)∪scaleTo(P，0.1)。转化后的结论图如图1所示。

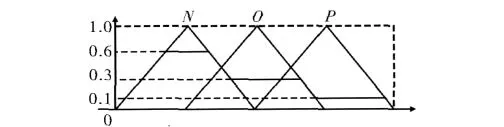
图1 加权复合结论

转化后的加权复合结论，保证了结论各项依靠其权重影响推理结论，规则库的规模不发生变化，将复合结论作为规则结论，然后作进一步推理。

2 基于置信规则的模糊推理算法

基于规则库中的一系列规则，推理机按照一定的推理策略，求解所提出的专门问题。分别给出针对置信规则前提和结论部分的计算方法，把前提属性权重融入推理过程，规则的分布式结论转化为模糊集，基于这两种计算方法，给出一种基于置信规则的模糊推理算法。

2.1 算法思想

置信规则的特点是，依据专家经验加入了前提属性权重、规则权重以及分布式结论，规则描述更符合实际应用。基于置信规则的模糊推理算法，对前件和后件分别做预处理，结合Mamdani算法的推理过程进行推理。

首先，根据输入事实，运用Mamdani方法进行规则合成运算，得到单个前件的匹配度，并根据前件的置信度，为每个前件分配一个“相对重要程度”，对所有单个前件匹配度加权求和，得到“整体前件匹配度”;其次，以分布式评价的各项置信度作为权重，将相应模糊子集加权合并，把加权复合结论作为规则结论;最后，运用Mamdani推理的规则计算，得到规则的模糊输出。

2.2 基于置信规则的模糊推理算法流程

当输入信息到来时，根据提出的计算方法，对前件和后件作预处理，分别计算整体前件置信度和置信规则结论转化，从而得到最终输出。算法流程如下:

(1)计算适配度。把事实与模糊规则的前件进行比较，求出事实对每个前件的适配度ωAi。

(2)计算整体前件置信度。为每个前件分配一个“相对重要程度”，然后计算“整体前件匹配度”s

(3)计算分布式结论。以置信规则分布式结论的各项置信度为权重，将相应模糊子集加权合并，D*=scaleTo(D1，β1，k)∪scaleTo(D2，β2，k)∪…∪scaleTo(DN，βn，k)，把合并后的模糊集 D*作为复合结论。

(4)计算规则的模糊输出。用“整体前件置信度”与转化后的复合结论依据Mamdani规则运算，即μD*(z)=s∩μD(z)，得到该条规则的模糊输出μD*(z)。

(5)计算总输出。将所有规则有效后件μD*(z)进行综合，求并集，得到总输出μ(z)。

下面以两前件两结论的规则为例，对该算法进行

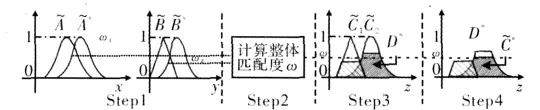
图2 基于置信规则的推理算法的推理过程

首先，根据输入事实与模糊关系合成得到单个前件的匹配度ωA，ωB，根据前件的置信度为每个前件分配一个“相对重要程度”;其次，对前件匹配度进行加权求和得到“整体前件匹配度”ω=;然后，以分布式评价的各项置信度作为权重，将模糊变量作加权合并的复合结论作为规则结论D*=scaleTo(C～1，δ1)∪scaleTo(C～2，δ2);最后，通过规则计算得到该条规则的模糊输出。

3 模糊推理算法在实例中的验证

在水下作战中，潜艇被鱼雷发现时，鱼雷规避系统［9］根据设备提供的鱼雷、诱饵、干扰机等信息，运用专家系统工具推理决定诱饵、干扰机的下一步工作，诱骗或干扰鱼雷，使潜艇能够安全躲避鱼雷攻击。

仿真中，分别使用专家系统工具FuzzyCLIPS和扩展后的FuzzyCLIPS进行推理，扩展的FuzzyCLIPS将传统的模糊规则描述扩展为置信规则，模糊推理模块使用基于置信规则的模糊推理算法。假设潜艇使用诱饵后，鱼雷总是去追赶诱饵，两者距离超过一定界限，鱼雷判断是否为潜艇，如果不是潜艇，鱼雷不会爆炸，再次搜寻潜艇。假设潜艇使用了干扰机，鱼雷无法检测到潜艇，在原处停留，当干扰关闭后，鱼雷再次搜索潜艇。

鱼雷规避仿真的规则库采用由置信规则组成:

Rule4:IF Torpedo Warning(1.0)and Decoy Empty(0.5)THEN Move_Quietly_Against_Torpedo_Direction(CF 0.8)

Rule5:IF Torpedo Danger(1.0)and Decoy Empty(0.5)and Jammers Full_Ready(1.0)THEN Fire_Jammers_AND_Load_Jammers and Move_At_Full_Speed_A-gainst_Torpedo_Direction(CF 1.0)

根据专家经验，鱼雷的距离越近，对潜艇的威胁程度越大，因此规则权重设置越大，故Rule5的规则权重为1.0，Rule4的规则权重为0.8。不同的前提属性对于推理结果也是至关重要的，Rule5中的鱼雷对潜艇的威胁程度严重，诱饵状态为空，干扰机的状态为充分准备好，鱼雷的威胁程度和干扰机的状态对于推理结果相对于决策更加重要，权重为1.0;诱饵的状态对推理结论并不造成严重影响，权重设置为较小的系数0.5。

仿真系统中，使用3个输入变量:鱼雷与潜艇的距离d，诱饵的状态ds，干扰机状态js。

在仿真中，潜艇发现鱼雷的距离分别设置为1 425 m、1 450 m、1 475 m、1 500 m，每个距离仿真100次，每次仿真中鱼雷和潜艇的初始距离设置12.5 m的随机误差。假设潜艇的常规运行速度为5节(1节=1.852 km/h)，最大速度12节;鱼雷航程10 000 m，速度40节;诱饵速度17节，干扰机工作时间30 s;潜艇配备1个诱饵，一对干扰机。

仿真分别使用基于传统规则的FuzzyCLIPS和基于置信规则的ExFuzzyCLIPS专家系统工具，以下是不同距离上鱼雷规避成功的概率分布情况，如图5所示。

图5 潜艇鱼雷攻击FuzzyCLIPS和ExFuzzyCLIPS的生存可能性

根据图5分析，当规避的决策使用FuzzyCLIPS推理时，直到发现距离增加到1 450 m也没有存活的可能性。使用扩展的FuzzyCLIPS推理，当距离＞1 425 m后，规避成功的概率＞0;在1 475 m附近成功概率也都大于FuzzyCLIPS。通过对实验结果分析得出结论，使用扩展的FuzzyCLIPS推理比原有FuzzyCLIPS可以获得较为乐观的决策方案，增加了受到鱼雷攻击时潜艇生存的可能性。

仿真使用ExFuzzyCLIPS推理时，选用两组前件属性权重和规则权重不同的置信规则，置信规则库1的规则权重全部为1，认为所有规则对于决策结果同等重要;置信规则库2的规则，根据距离威胁程度的对规则权重作相应的调整，警告状态下规则权重0.8，危险状态下规则权重1.0。从图中可以看出，置信规则库1在1 450 m和1 475 m附近的成功概率大于置信规则库2，而在1 500 m附近却小于置信规则库2。因此，在使用扩展的FuzzyCLIPS做推理工具时，置信规则中的权重参数对推理结果的有重要的影响。

4 结束语

针对专家系统中模糊规则的局限性，提出了基于置信规则的模糊推理算法，该算法支持多种输入形式，既可以是定量信息，也可以是定性知识。一方面，算法将根据专家经验获得的前提属性权重和规则权重融入推理过程，并且将事件的模糊性与随机性融入推理过程;另一方面，把置信规则的分布式结论依权重合并，既保留了权重对结论的影响，又不增加规则库的规模。将基于置信规则库的模糊推理算法引入FuzzyCLIPS，把扩展后的FuzzyCLIPS应用到鱼雷规避系统中，仿真结果表明，基于置信规则的模糊推理方法提高了潜艇在受到鱼雷攻击时安全逃离的可能性。仿真中的置信规则的选择，对决策结果有较大影响，置信规则的权重参数依赖于专家经验，有较强的主观性，因此，如何训练学习置信规则的权重参数，使其能够离线优化，有待展开更深一步研究。

［1］周影辉，徐亮，韦博成.基于Bayes方法的诊断模型分析［J］.高校应用数学学报:A 辑，2008(3):268－276.

［2］熊卫.Dempster_Shafer证据理论及其解释［J］.华南师范大学学报:社会科学版，2000(3):15－21.

［3］ZADEH L A.Outline of a new approach to the analysis of complex systems and decision processes［J］.IEEE Transactions on Systems Man and Cybernetics，1973，3(1):28 －44.

［4］王永庆.人工智能原理与方法［M］.西安:西安交通大学出版社，1998.

［5］哈艳.CRI方法与基于相似性推理方法在分类问题中的比较研究［D］.河北:河北大学，2006.

［6］ZHOU Z J，HU C H，CHEN M Y.An improved fuzzy kalman filter for state estimation of nonlinear systems［J］.International Journal of Systems Sience，2010，41(5):537 －546.

［7］周志杰，杨剑波，胡昌华，等.置信规则库专家系统与复杂系统建模［M］.北京:科学出版社，2011.

［8］ZADEH L A.Outline of a new approach to the analysis of complex systems and decision processes［J］.IEEE Transactions on Systems Man and Cybernetics，1973，SMC －3:28 －44.

［9］MYEONG J S，TAE W K.Torpedo evasion simulation of underwater vehicle using fuzzy－logic－based tactical decision making in script tactics manager［J］.IEEE Trance on Communication，2012，39(9):7996 －8012.