基于LBM动态动画真实感绘制

黄 瑞

(华北水利水电学院信息工程学院，河南郑州 450011)

自然景物模拟一直是计算机图形学中最具挑战性的问题之一。关于流体现象的模拟，在计算机动画游戏、影视特效、虚拟仿真等方面有着重要的应用。简单的粒子系统方法［1］很难满足真实感的要求，而遵循流体真实运动规律的、基于物理的模拟方法无疑是最能满足真实性要求的。

基于物理的流体模拟主要依据是计算机流体力学原理。目前通过求解经典N－S(Navier－Stokes)方程的模拟方法，国内外学者已经做了大量的研究。但由于N－S方程是基于连续介质假设，因此对自由表面流体的离散和扩展存在困难。

文中主要采用LBM(Lattice Boltzmann Method)方法对流体和烟雾进行模拟。Kass［2］最早提出浅水方程的思想，将流体高度假设为各个点的宏观密度，再基于高度生成水面;Zhou［3］等在LBM 的D2Q9网格中求解浅水方程，完成了溃坝模型的数值模拟;Liu［4］等还提出了在多重网格下来实现潜水方程，即在需要更多细节的地方人为地划定密集的网格，从而在小运算量下得到较好的表现效果。另外，基于粒子系统和Lagrange方法的光滑粒子流动力学方法也是比较流行的方法，它具有容易实现、善于表现细节的优点，缺点是表面构建困难，平滑核函数难以选取。

在2002年，Wei［5］将LBM方法引入流体图形仿真并首先模拟了火焰，随后又模拟了空气中的烟雾［6］;Zhao［7］基于LBM模拟了固体的融化现象和基于热流体的蜃景。LBM方法能够方便地处理复杂边界与障碍物的流体［8］，也可以用来模拟多相流体［9］。

1 LBM方法相关理论

近年来，流行于计算机流体领域的LBM方法，提供了另一种流体力学表现方法。其主要思想是基于大量时空离散的微观粒子之间的碰撞迁移，并利用这些微观粒子运动的统计平均结果来反映流体现象的宏观特征。该方法具有物理图像清晰，边界条件容易处理，并行性能好等优点。目前，LBM在多相流、化学反应扩散、多孔渗流、粒子悬浮流、磁流体学等相关领域也得到了成功的应用。

在LBM模型中，每个格点有9个不同方向的平衡分布函数，如图1所示。微观粒子会根据特定运动规则在离散格子上进行迁移和碰撞，而迁移过程表示的是通过粒子运动的统计平均就能得到流体的宏观运动特征。

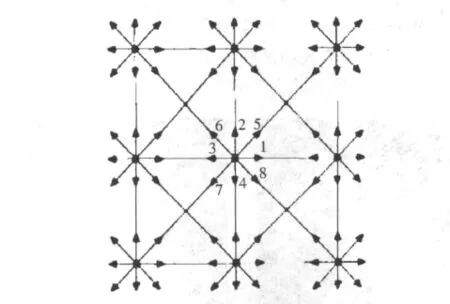
图1 方格上的D2Q9模型

一般LB方程可以分解为两个部分:

(1)碰撞项

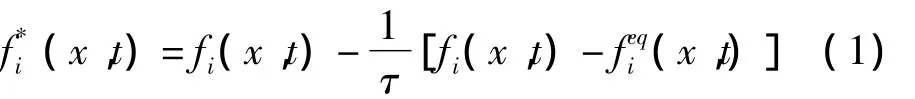
(2)迁移项

粒子的平衡态分布函数为

不难看出，图1和图 2刻画的是始源和目标的结构，基于始源和目标之间的映射、迁移的过程就是借助概念网络将两个概念体系刻画出来的过程,也是人工智能中知识表达的过程。

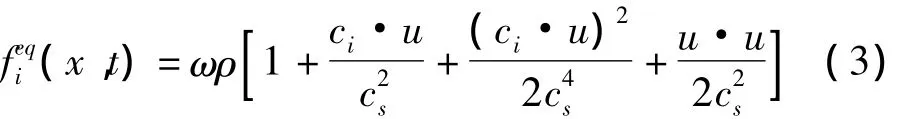
其中，τ为弛豫时间，反应非平衡态趋于平衡态的快慢;feqi为平衡分布函数;ρ为介质的宏观速度;u为宏观速度;i为粒子的不同离散速度的方向。

宏观方程和宏观速度为

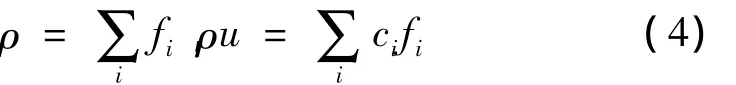
LBM方法可以容易地处理边界。在边界处的格点上，密度分布中速度方向指向边界的是不能穿过边界的，因此需要定义一种边界条件来处理所有处于边界格点的平流速度。常见的边界处理格式有启发格式、动力学格式、外推格式和复杂边界处理格式。

LBM的计算流程:(1)设置初始条件如每个格子的密度、速度、压强等，选择合适的弛豫时间。(2)对每个格子用式(4)计算其宏观密度和速度。(3)用式(3)计算平衡态分布函数。(4)把格子分布函数和平衡态分布函数代入式(1)。(5)根据步骤(4)的结果，对各个相邻格子进行相应的调整。(6)根据边界条件来调整分布函数。(7)返回步骤(2)进行循环，直到流场达到收敛要求。

2 基于LBM的建模

2.1 基于LBM的洪水演变

浅水动力学方程组与普通二维流体力学方程不同［10］。它考虑对象为均质不可压缩流体，因此方程中不出现密度，取而代之的是自由表面高度h，如图2所示。侧面压力项是由于流体质量水平分布不均匀的重力效果造成的，因此形式上也不同于普通流体力学方程中的压强。所以必须重新构造适合于模拟浅水运动的模型。

图2 溃坝波形示意图

经典的二维浅水方程可以表示为

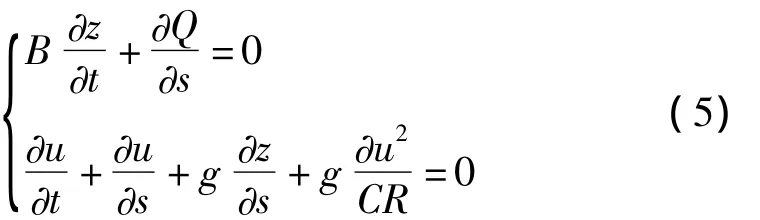
文中模拟了二维水坝溃决，模拟区域为50 m×50 m，中间用拦水坝分成相同的两部分，采用上游水位为8 m，下游水位为4 m，不考虑摩擦、坡度等外力因素。初始时刻的速度为零，假设水坝突然完全崩溃，上、下游水位出现突变，从而激发出一个向下游推进的水激波，在波前是未扰动的静止流体，波后流体才有速度，但流速远小于波速。固壁边界采用无滑的边界条件。在10～25 m处发生溃坝的模拟结果如图3所示。

2.2 基于LBM的烟雾模拟

烟雾同其他无规则的物体如云和火焰一样，具有实时多变性和无规则性。由于其外观形状极不规则、又没有光滑的表面，使得经典的欧几里得几何学很难对它进行描述。近几十年来不同学者已经提出了很多烟雾模拟的方法，其中的一些模型正趋于成熟，应用的领域也在不断延伸。但由于种种原因，目前普遍认为比较满意的使用方法还比较有限，通用性都或多或少地受到一定限制，很难说哪种方法更适合人们的要求。因此对于计算机工作人员，特别是图形图像处理的研究者来说，不断探索和改进目前的模拟理论和方法，发展出新的更便于使用的模拟方法，把现有各种方法的优点结合起来，更好地满足时代发展的需要，仍是重要课题，也是人们长期进行探索的重要方向。

烟雾是一种气固混合物，因此需要建立模拟气固两相流的格子Boltzmann模型，该模型中使用一种新型的耦合格子Boltzmann模型来刻画烟雾流体中气相与颗粒间的作用力。此模型需要加入烟雾流场的计算。

图3 洪水演变模拟

故此模型的演化方程变为

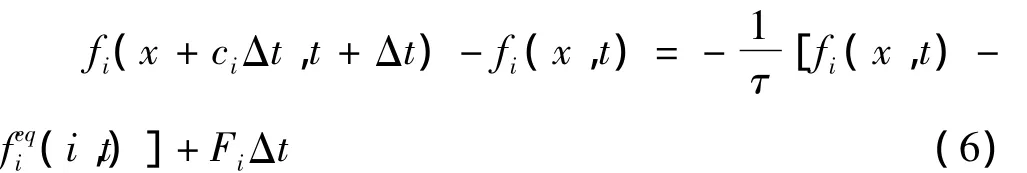
其中，Fi的表达式为

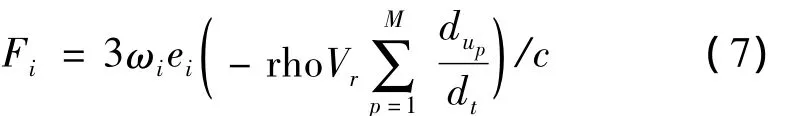
rho是颗粒相的密度与流相密度之比，试验中假设其值为10，M为控制体内颗粒的数目。采用非平衡外推格式进行边界处理，进而生成基于LBM的烟雾模拟，在WindowsXP环境下和VS2010+OpenGL平台上实现了简单的烟雾模拟系统。采用光线投射算法绘制密度，得到了较逼真的表现效果，如图4所示。

图4 烟雾模拟

3 实例分析

基于LBM方法并结合浅水方程对流体建模，实现了洪水演变的真实感绘制。文中的方法能够处理外力的相互作用，使用范围比较广，模拟速度也比较快。模型适用于并行计算，加之算法具有结构简单，容易编程实现，易于修改和移植等优点，因而在海洋湖泊和环境污染等领域有着广泛的应用前景。动态烟雾的成功模拟，对算机动画游戏、影视特效、虚拟仿真等有着重要的应用。

通过流体建模和表面高度场的计算，得到了较为真实的洪水演变模拟;简化了速度场方程组并添加了浓度场方程组，结合这两者对烟雾运动物理模型进行了改进。

4 结束语

过去计算机图形业一直专注于制造烟雾、燃烧、流水等自然现象的真实效果，而目前开始转向设计创作面部表情、毛发和衣服运动的真实模拟［10］。但对于无规则物体和常见自然现象的模拟，业内还在不断研究，设计开发出一种真实、实时、高效、交互性和通用性的烟雾模拟方法和实用软件，是人们的目标。可以说，要用计算机来有效地模拟自然景物，还有很多问题值得更加深入细致地研究。

［1］费少梅，彭艳莹，陆国栋，等.基于粒子的湍流燃烧火焰的可视化研究［J］.算机辅助设计与图形学学报，2005，17(3):461－466.

［2］KASSM，MILLERG.Rapid，stable fluid dynamics for computer graphics［J］.Computer Graphics，1990，24(4):49 －55.

［3］ZHOU J G.A lattice boltzmann model for the shallow water equations［J］.Computer Methods in Applied Mechanics and Engineering，2002，191(32):3527 －3539.

［4］LIU H F，ZHOU JG，BURROWSR.Multi－ block lattice boltzmann simulation of subcritical f low in open channel junctions［J］.Computers ＆ Fluids，2009，38(6):1108 －1117.

［5］WEI X M，LI W，MUELLER K.Simulating fire with texture splats［C］.Washington D C:Proceedings of the Conference Visualization，IEEE Computer Society Press，2002:227 －234.

［6］WEI X M，LIW，MUELLERK.The lattice boltzmann method for simulating gaseous phenomenon ［J］.IEEE Transactions on Visualization and Computer Graphics，2004，10(2):164－176.

［7］ZHAO Y.Modeling natural phenomena with lattice boltzmann method［D］.New York:State University of New York，2006.

［8］MEI R W，LUO L S，SHYY W.An accurate curved boundary treatment in the lattice boltzmann method ［J］.Journal of Computational Physics，1999，155(2):307 －330.

［9］朱红斌，刘学慧，柳有权，等.基于Lattice Boltzmann模型的液－液混合流模拟［J］.计算机学报，2006，9(12):2071－2079.

［10］肖诗云，王晓庆.洪水演进模型及冲击荷载数值分析［J］. 工程力学，2010，27(9):35－40.