二维几种常见阵型阵列的阻塞矩阵构建

王 纯，董娟娟，徐婷婷，罗 丰，孙燕妮

(1.西安电子科技大学雷达信号处理国家重点实验室，陕西西安 710071;2.西安建筑科技大学信息与控制学院，陕西西安 710055;3.陕西电子工业研究院，陕西西安 710065)

众所周知，阻塞矩阵的构建涉及强干扰背景下微弱信号 DOA 估计［1－2］、广义旁瓣相消(GSC)阵列［3－4］等领域。一维线阵虽然结构简单、易于分析，但检测估计的结果只有方位角而没有俯仰角。相对于一维线阵，二维阵型的研究，其更加符合实际环境和工程应用，也更具针对性。这就需要通过二维阵型得到更丰富、准确的信息。因此，建立不同二维阵型的二项式对消阻塞矩阵［3］的研究具有重要的研究意义和实用价值。

以下分别介绍圆阵、面阵、Y阵、十字阵、L阵的阻塞矩阵建立方法，并以此为例总结出普适性的构造二维阻塞矩阵的方法——一字阶梯累积法。

1 信号模型

考虑Q个远场窄带信号入射到空间某阵列上，包括J个干扰和P个信号。方位角和俯仰角为(θi，φi)，其中，i=1，2，…，Q。

阵列天线由M个阵元组成，这里假设阵元数等于通道数，假设阵列中各阵元是各向同性的且不存在通道不一致、互耦等因素的影响［4］，噪声为相互独立的零均值高斯白噪声，且与信号不相关。则阵列的接收数据模型为

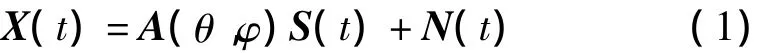
其中，X(t)=(x1(t)，x2(t)，…，xM(t))T。列接收数据向量;A(θ，φ)为阵列流形，A(θ，φ)=(a(θ1，φ1)，a(θ2，φ2)，…，a(θQ，φQ))信号 s(t)=［s1(t)，s2(t)，…，sQ(t)］T为入射信号矢量，N(t)为阵元接收加性高斯白噪声，N(t)=［n1(t)，n2(t)，…，nM(t)］T。其中，T表示转置;λ表示入射信号载波波长。

以下是经过推导，获得的基于几种常见阵型的二项式对消阻塞矩阵的构建。

2 圆阵阻塞矩阵的构建

M 个阵元的圆阵［5－6］干扰导向矢量为

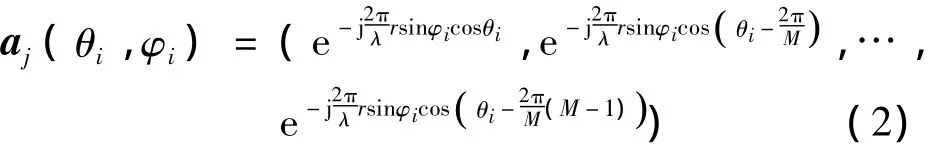
其中，i=1，2，…，J。现构造阻塞矩阵 B，使得 B ×aj(θi，φi)=0。假定干扰个数 J=1，推理后得到

3 面阵的干扰阻塞矩阵构建

M阵元的面阵，其干扰导向矢量为

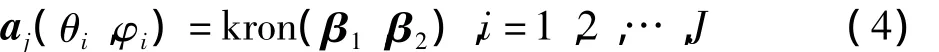
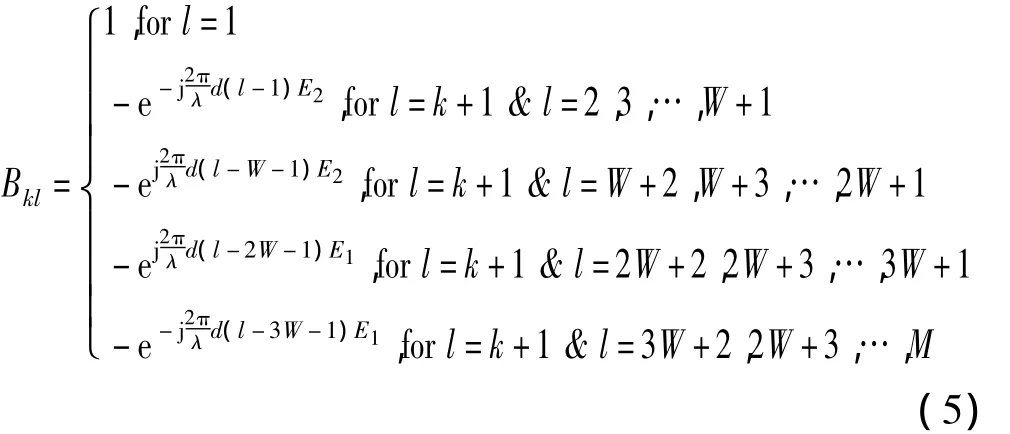
其中，行数k和列数 l分别取 k=1，2，…，M －1;l=1，2，…，M;W=－1。可以看到，为使W取整数要求阵元个数M的平方根是整数。

4 Y阵的干扰阻塞矩阵

考虑如图1所示的均匀M阵元的Y阵，其干扰导向矢量为

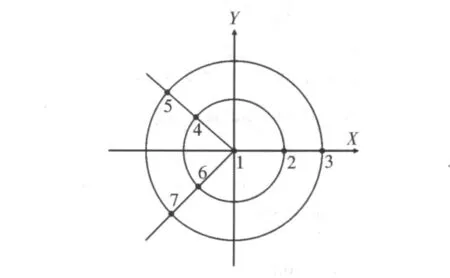
图1 Y阵阵列模型

现构造阻塞矩阵 B，使得 B ×aj(θi，φi)=0。假定干扰个数J=1，推理后得到

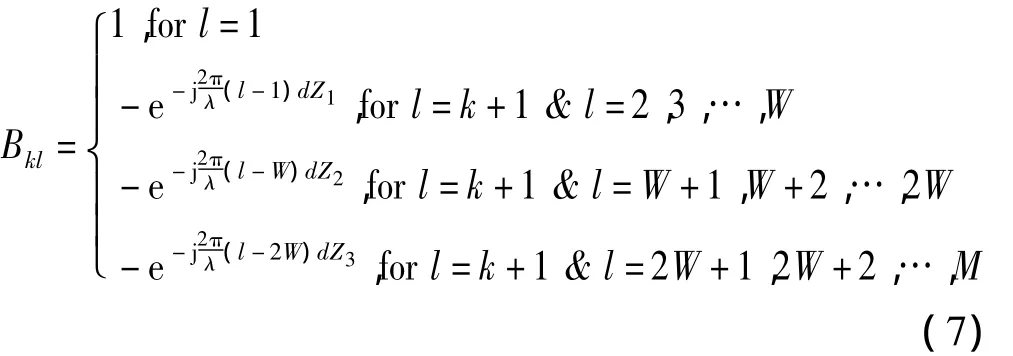
其中，行数 k 和列数 l分别取 k=1，2，…，M －1;l=1，2，…，M;Z1=cosθisinφi;Z2= － sin45°cosθisinφi+cos45°sinθisinφi;Z3= －sin45°cosθisinφi－cos45°sinθisinφi。

5 十字阵的干扰阻塞矩阵构建

如图2所示的M阵元的均匀十字阵，其导向矢量为

图2 十字阵阵列模型

其中，k=1，2，…，M －1;l=1，2，…，M。

6 L阵的干扰阻塞矩阵构建

如图3所示的M阵元的L阵，其导向矢量为

为使W取整数要求阵元个数M －1 是2 的倍数。E1=cosθisinφi;E2=sinθisinφi。

图3 L阵阵列模型

构造阻塞矩阵B，使得B×aj(θi，φi)=0。假定干扰个数J=1，推理后得到

其中，k=1，2，…，M －1;l=1，2，…，M。

通过构造以上几种常见二维阵型阻塞矩阵的规律可以看出，凡是导向矢量第一项为1的阵型，都可用上述方法构造相应的阻塞矩阵，由于该方法构造的阻塞矩阵的特点是第一列全为1，且呈现阶梯累积形式，故形象取名为一字阶梯累积法。

7 仿真验证

为对阻塞效果进行验证，做如下仿真。仿真条件:假定有一个干扰来波角度为(θj1，φj1)=(60，30);阵元数为9;半径波长比为0.5;其导向矢量由上述已知为aj(θj1，φj1)，若 B × aj(θj1，φj1)=0，则证明干扰阻塞成功。仿真结果如表1～表3所示。

表1 面阵圆阵阻塞矩阵阻塞效果

表2 Y阵、十字阵阻塞矩阵阻塞效果

表3 L阵阻塞矩阵阻塞效果

由表1～表3可以看出，导向矢量经过阻塞矩阵后被阻塞为0，即B×aj(θj1，φj1)，即干扰得到了有效抑制。

8 结束语

对二维几种典型的常用阵型的阻塞矩阵构建做了分析、推导和说明，并在此基础上总结出了具有一般普适意义的二维阻塞矩造方法——一字阶梯累积法。经仿真验证，该方法简单有效。

［1］王永良，陈辉，彭应宁.空间谱估计理论与算法［M］.北京:清华大学出版社，2004.

［2］陈辉，苏海军.强干扰/信号背景下的DOA估计新方法［J］.电子学报，2006，4(3):530 －534.

［3］王纯，张林让，陈广锋，等.用于GPS接收机的快速自适应干扰抑制方法［J］.西安电子科技大学学报:自然科学版，2011，38(3):114 －120.

［4］王永良，丁前军，李荣锋.自适应阵列处理［M］.北京:清华大学出版社，2009.

［5］黄珂.均匀圆阵列参数分析［J］.电子科技，2012，25(5):8－10.

［6］曾耀平，齐云.空间非平稳噪声下圆阵的DOA估计［J］.电子科技，2008，21(2):76 －78.