基于解卷积的频域光学相干层析像质优化

万忠启，刘国忠

(北京信息科技大学仪器科学与光电工程学院，北京 100192)

光学相干层析成像(OCT)是继超声断层成像、X光断层成像和磁共振成像(MRI)之后，一种新的医学诊断技术，其具有μm级的分辨率［1］。光学相干层析成像分为时域OCT和频域OCT，但由于时域OCT是通过移动参考臂的反射镜对样品进行扫描，因此不可避免地造成信噪比下降，而频域OCT无须参考臂的扫描就可以获得较高的纵向分辨率。

在图像处理的应用中，清晰的图像往往难以直接得到，此时需要应用图像复原原理对图像进行处理。常用的图像复原方法包括正则化约束最小二乘法、非均匀插值法、凸集投影法、贝叶斯(Bayesian)方法等［2－3］。文中介绍的图像复原处理方法，首先针对CCD采集的频谱进行包括傅里叶逆变换在内的各种预处理，然后再运用高斯函数点扩展函数进行Lucy－Richardson解卷积方法处理，最后对图像进行改进直方图均衡算法的深层有用信息增强操作，提高图像的纵向分辨率。

1 复谱频域成像

1.1 成像原理

频域OCT技术主要是光谱仪接收宽带光源的光谱干涉，其中光谱仪包括光栅、聚焦透镜和CCD接收器。图1所示为整个复谱频域OCT的原理图。

图1 频域OCT原理图

在频域OCT系统中，光源采用中心波长为838 nm，半高全宽为50 nm的低相干光，光谱仪模块分别采用焦距f为60 mm的聚焦透镜，1 200 line/mm的光栅和包含2 048个像素、线频扫描率为29 kHz的高速线阵CCD。该系统的最重要部分是带有50/50分光器的迈克尔逊干涉仪，它将宽带光源所发出的光分成样品光和参考光，两束光返回形成的干涉信号被光谱仪所接收，得到的干涉光谱I(k)为

其中，Ts和Tr表示分光器的样品臂和参考臂的透射系数;k表示波数;s(k)表示照射光源的强度谱;r(h)表示反射系数。式(1)的前两项分别是参考光和样品光的自相关项，即表示干涉光谱的直流项，最后一项是二者的互相关项，它反映了样品深度信息，其中每个余弦函数的幅度与样品深度的反射系数r(h)成正比。由于样品后向散射的样品光比较微弱，其自相关项可忽略不计，因此，式(1)可简化为

1.2 复谱域数据预处理

由式(2)可知，干涉光谱包含一个直流量和样品深度信息，若想获得样品深度信息，必须从二维图像数据中减去干涉光谱的直流项。去掉直流项后的复域光谱为

∫+∞I(k)=TsTrs(k)02r(h)cos(2knh)d h(3)

此时的图像数据是以幅度为基础的强度谱，对该强度谱进行快速傅里叶逆变换，即可得到包含深度信息的空域纵向横截图。

2 解卷积及改进直方图均衡理论分析

解卷积是后处理常用的一种方式［4］，通过波前传感器可以得到光学系统的点扩散函数(PSF)，利用PSF可以对图像做解卷积处理［5－7］。图像解卷积的实现方法有多种，如最小二乘法、Richardson－Lucy算法、极大似然概率估计等，选择合适的解卷积方法能有效改善图像的分辨率，文中提出了一种基于 Lucy－Richardson解卷积和改进直方图均衡算法的像质优化处理方法:针对CCD采集的频谱进行预处理后得到的空域图，运用高斯点扩展函数进行Lucy－Richardson解卷积方法操作，然后运用改进的直方图均衡算法对图像进行增强处理，从而得到具有较高纵向分辨率的图像。整个图像处理的实现流程如图2所示。

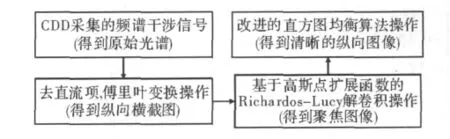
图2 图像处理流程图

2.1 Lucy－Richardson解卷积迭代算法

Lucy－Richardson迭代算法是目前应用比较广泛的复原算法之一，其能够按照泊松噪声的统计学原理标定点扩展函数PSF，并与之进行卷积获得复原图像。将式(3)改写成 FT(I(k))=FT(S(k))×obj(z)，令psf(z)=FT(S(k))，也可以改写成obj(z)=psf(z)×obz(z)，式中，“* ”表示卷积运算，obj(z)为重建的纵向深度信号;obz(z)为样品纵向反射分布函数;psf(z)为高斯点扩展函数。

为得到清晰的图像，采用Lucy－Richardson迭代算法恢复图像。Lucy－Richardson迭代算法是一种按照泊松分布和最大似然法进行估计的基于贝叶斯分析的迭代算法，其迭代方程可表示为

其中，“*”和“·”分别表示卷积运算和乘积运算;k为迭代次数，在迭代方程中，假设obz(z)的初值obz(0)=obj(z)，经过证明可得，在忽略噪声影响的情况下，随着迭代次数k的增加，真实清晰图像函数f是收敛函数，因此可以恢复出原始图像。

2.2 改进的直方图均衡算法

直方图均衡化算法是依据一幅图的像素灰度级，对变换前后的灰度值进行均匀分布，从而得出灰度值的均匀分布函数。对于像素点离散的图像，原始灰度值i的转换规则为

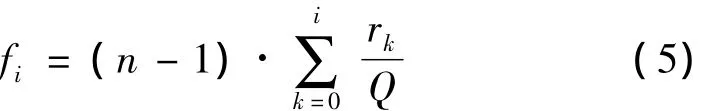
其中，n表示离散图像矩阵的灰度级数;rk表示离散图像矩阵中灰度值为k的像素数;Q为图像像素总数。上述方法能将离散像素的灰度值重新均匀分布，改善图像质量，但当图像像素的灰度动态范围小、散斑噪声大、灰度级较少时，该均衡方法容易将微弱的深层有用信息和散斑噪声混淆，覆盖掉图像的部分有用信息，影响图像的质量。因此，需要改进传统的直方图均衡化算法。

为在图像恢复过程中保留部分有用信息，根据相邻像素灰度值i和i+1进行局部灰度均衡化，摈弃了在整体均衡化时容易忽略部分相近灰度值、散斑噪声灰度值和有用信息灰度值相差小的缺点，保证了图像相邻像素灰度的完整性。假设图像中灰度值i具有的像素数为ri， 经过具有单调变化性质的函数映射后变为r'i，像素总数Q变成，此时转换规则变为

式(6)得到的新灰度值分布于整个灰度空间，即扩展了所使用的灰度空间。

整个程序结构简述如下:(1)初始化相关的参数和变量，依次读入计算的图像。(2)根据每个图像像素的灰度值，对应计入灰度像素个数累加器ri。(3)选取合适的映射关系对像素个数及灰度值进行转换，增大散斑噪声灰度值和微弱的深层有用信息灰度值间隔。所以，文中选用具有单调递增关系的对数函数，即ri=ln(ri+1)，分别计算出 r'i和新的像素总数 Q。(4)由式(6)依次计算出图像原始灰度值i经过转换后的灰度值fi。

经过变换规则公式所形成的灰度值fi，逐次组合构成图像矩阵，即为变换后的增强图像。在全部的计算过程中，为提高计算的准确性，可以将像素总数Q设定成浮点型变量。

3 实验结果与讨论

复谱频域OCT实验结构如图1所示。在本实验数据采集中，样品采用洋葱上表皮组织。图3(a)表示原始的纵向横截面图像。图3(b)表示运用Lucy－Richardson迭代解卷积算法后的图像。图3(c)表示使用改进的直方图均衡算法后的图像。从图3(a)可以看出，洋葱上表皮组织的细胞壁有散焦情况，图3(b)是沿着深度方向聚焦所形成的图像，相比图3(b)，图3(c)将微弱的深层有用信息从散斑噪声中分离出来，恢复出更深的组织散射信号，便于观察深层细胞结构。

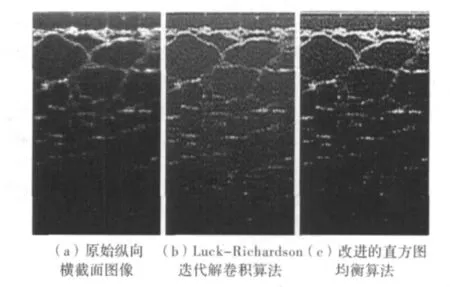
图3 图像处理结果对比

4 结束语

文中提出了一种基于高斯点扩展函数的Lucy－Richardson解卷积方法，该方法能沿样品的深度方向对模糊失真的横截面图像进行聚焦操作，恢复样品的细节结构;然后采用改进直方图均衡化算法拉大了散斑噪声灰度值和深层有用信息灰度值的间隔，增强了纵向横截面图像深层信息的灰度值，即从散斑噪声中分离出有用信息，还原出更深的结构。这些方法能有效地提高图像的纵向分辨率，适合复杂的组织层析成像，并且在深度位置上信息复原正确，所以该工作对复杂生物组织图像的复原具有一定的价值。

［1］HUANG D，SWANSON E，LIN C，et al.Optical coherence tomography［J］.Science，1991(254):1178 －1181.

［2］CHEN W F，CHEN M，ZHOU J.Adaptively regularized constrained total Least－ squares image restoration［J］.IEEE Transaction on Image Processing，2000，9(4):588 －596.

［3］冈萨雷斯·伍兹.数字图像处理［M］.阮秋琦，阮宇智，译.2版.北京:电子工业出版社，2003.

［4］刘莹，何小海，陶青川，等.基于三维高斯模型的参数盲解卷积算法［J］.光电子·激光，2006，17(4):493－497.

［5］DAVID C，CHRISTOPHER D.High － resolution imaging ofthe human retina with a Fourier deconvolution technique［J］.JOpt Soc AmA，2002，19(8):1515 －1523.

［6］JUSTO A，SALVADOR B.Hybrid technique for high resolution imaging of the eye fundus［J］.Optics Express，2003，11(7):761－766.

［7］JULIAN C C，AUSTIN R，DAVID R.Deconvolution of adaptive optics retinal images［J］.Journal of Optimal Soc Am A，2004，21(8):1393 －140.