电动汽车电机驱动系统效率优化控制

周雅薇，聂建华

(安徽工业大学电气信息学院，安徽马鞍山 243000)

电动汽车以能源利用率高、环境污染小、噪音低等优点得到广泛关注。电机驱动技术和电池技术是电动汽车的核心技术。永磁同步电机以其高功率密度和高效率等优点，作为电动汽车首选电机并得到广泛应用。由于电池技术局限性，电动汽车一次续航里程有限的问题无法从根本上解决，因此提高电机驱动系统的效率成为解决该问题的有效途径［1－3］。

提高电动汽车永磁同步电机驱动系统效率方法有3种:完善电动机的设计、优化逆变器的输出波形及利用效率优化控制策略［1］。对于给定的永磁同步电机，通常采用效率优化控制策略提高系统效率。目前，研究的PMSM效率优化策略主要有基于损耗模型的效率优化控制策略(LMC)和基于在线搜索技术的效率优化控制策略(SC)。文献［2］采用黄金分割法来搜索最小损耗下的最优定子磁链值，该方法能快速寻找到最优定子磁链值，收敛速度较快，但起始阶段转矩波动大;文献［3］提出一种模糊逻辑自适应和黄金分割法相结合的混合搜索方法，有效提高系统效率，转矩脉动小，但系统结构复杂，在一定程度上影响了系统的响应速度。文献［46］建立了电机的损耗模型，通过数学方法求得最小损耗下的最优磁链值，从而达到降低系统损耗的目的，但由于电动汽车运行工况复杂，起动加速度频繁，造成电机参数变化大，使得损耗模型下的最优直轴电流和最优磁链难以准确计算［7］。

文中研究了基于损耗模型的永磁同步电机效率优化策略。针对电机运行过程中定子电阻的变化引起最优电流无法准确计算的问题，运用小波神经网络定子电阻观测器有效地在线估计出实时电阻值，使电流最优，进而使驱动系统效率达到最优。最后通过仿真验证了文中算法的有效性。

1 PMSM损耗模型的建模与分析

PMSM稳态运行时的损耗包括定子绕组电阻损耗、铁心损耗、机械损耗及杂散损耗。其中铁心损耗和定子绕组电阻损耗占总损耗的比重较大;机械损耗包括风摩损耗及轴承摩擦损耗，与电机电流和磁通量无关。为简化永磁同步电机的损耗模型，在d－q下建立只考虑铜损和铁损的电机损耗模型，等效电路如图1所示。

图1 中，ud、uq、id、iq分别为 d － q坐标系下定子电压和电流;Rs、RFe、φf分别为定子电阻、等效铁损电阻和永磁体磁链;iωd、iωq、iFed、iFeq分别为 d、q 轴上的电流有功分量和无功分量。

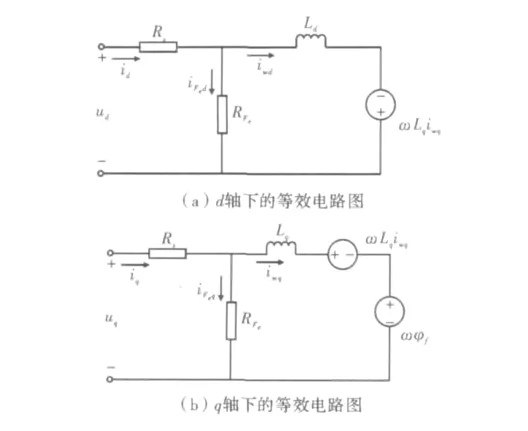
图1 d－q下PMSM等效电路图

由图1可得稳态下的电压方程、节点电流方程为

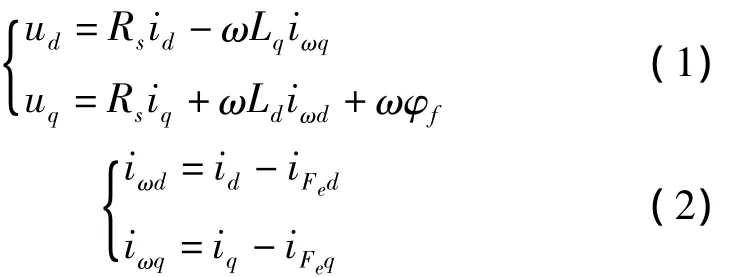
经整理后可得稳态时电机的铁损和铜损为

则总的电气损耗为

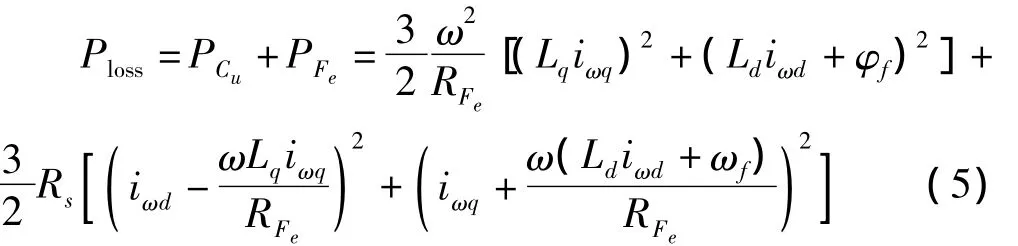
由于d、q轴上的磁链分量和电磁转矩的表达式为

将式(8)代入式(5)可得

考虑到在数字化系统中，采样周期较短，因此在每个采样周期内，可以认为Te和ω是恒定的。由式(9)可知，通过调节iωd可以使驱动系统的损耗最小。令可求得最小损耗时的最优电流i为ωd.opt

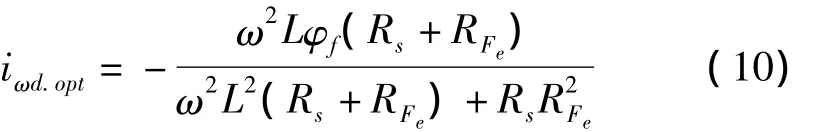
将式(10)代入式(6)和式(7)，可求得磁链分量φd和φq，则最小损耗下PMSM直接转矩控制系统最优磁链给定值φs.opt为

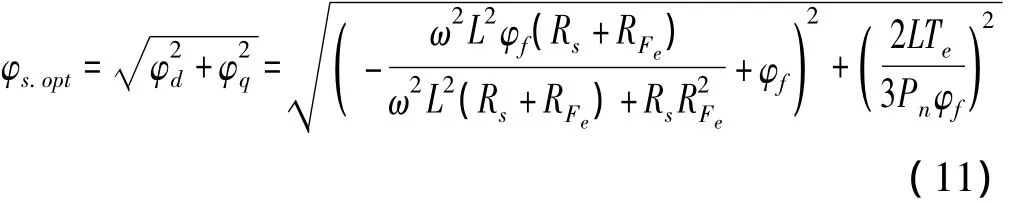
2 基于电阻补偿的PMSM最小损耗策略

电机运行过程中定子电阻随温度的变化而变化，由式(10)可知，将造成最优电流计算不准确，进而降低优化效果，因此，在损耗模型的基础上对定子电阻进行动态补偿，即可降低定子电阻对优化策略的影响，有效提高驱动系统的效率。

2.1 定子电阻动态补偿

由上述分析可知，在电机运行期间对定子电阻进行动态补偿，可改善系统的效率。文中采用小波神经网络定子电阻观测器在线实时观测出定子电阻的变化量，从而对定子电阻进行在线补偿。根据小波神经网络理论，构建小波神经网络定子电阻观测器，其结构如图2所示。

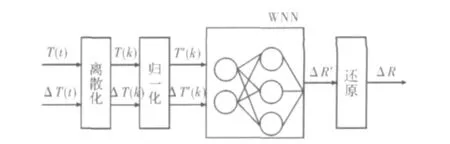
图2 定子电阻观测器的结构图

根据电机绕组最高温度确定定子绕组端部温度T的变化范围为0～110℃;温度变化率ΔT的范围为－3～+3℃/min;ΔR的变化范围为;0～2.3Ω。为便于处理和训练，将T、ΔT、ΔR做归一化处理。把温度T'和温度变化率ΔT'作为小波神经网络的输入量，输入到训练好的小波神经网络中，由此得出归一化的定子电阻的变化量ΔR'，进而得出ΔR，补偿后定子电阻值为R+ΔR。

2.2 小波神经网络的结构

把温度和温度变化率作为小波神经网络的输入量，将它们之间的关系定义为一个未知函数

通过小波神经网络辨识式(12)所示的两输入单输出的未知非线性函数关系，文中设计的网络结构如图3所示。

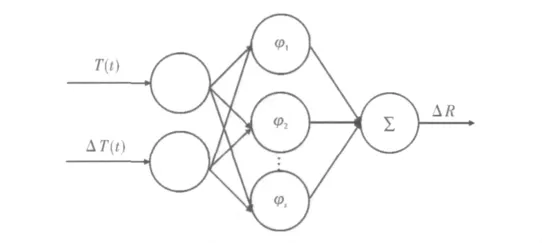
图3 小波神经网络的结构

网络的第1层将输入引入网络，第2层由小波元构成，执行小波变换，所有小波元组成一个非正交小波基。假设小波元的数量为s，所采用的小波母函数为Φ(x)，则第2层输入输出关系可表示为

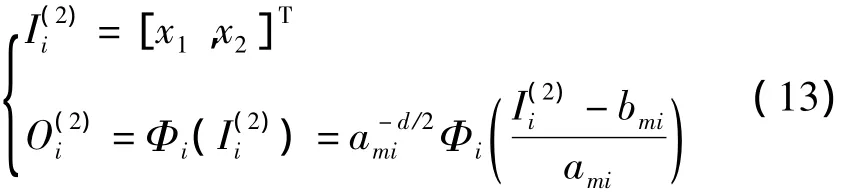
其中，I(2)i，O(2)i分别为第2层第i个神经元的输入和输出，i=1，2，…，s，参数 ami和 bmi为伸缩和平移系数，这里小波母函数采用墨西哥草帽函数，表达式如下

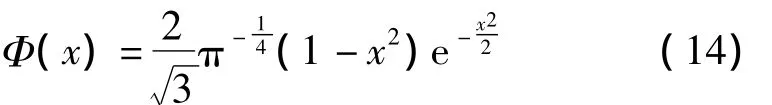
网络的第3层通过小波逆变换对网络描述的函数关系进行重构，得到网络的输出

其中，权值ωi为重构系数。

3 系统仿真实验

文中在Matlab Simulink平台上对基于效率改善策略的PMSM DTC系统进行了仿真实验。

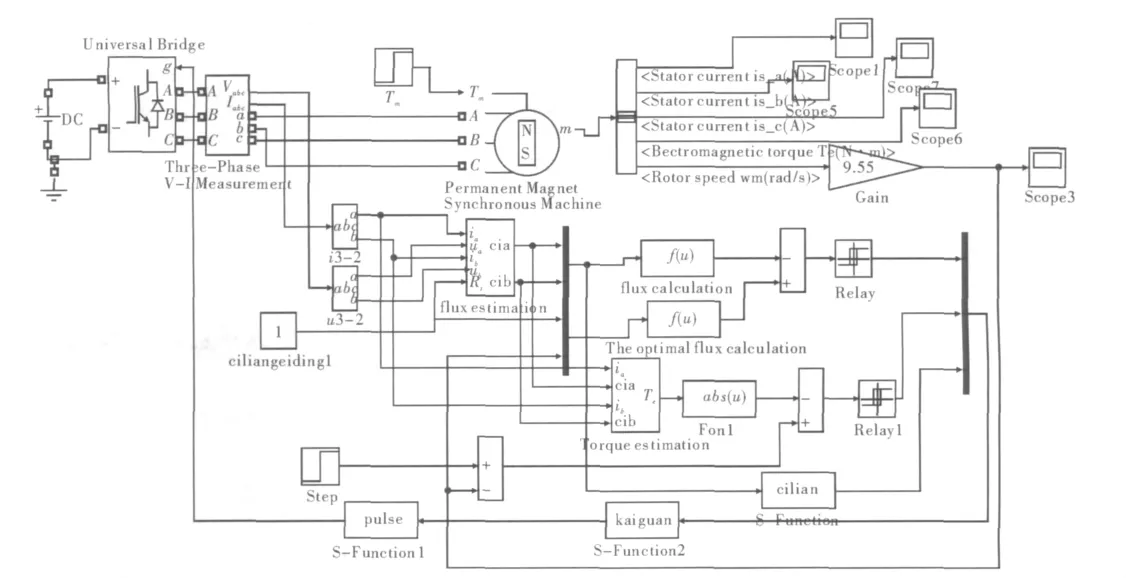
图4 系统仿真电路

仿真中采用的电机模型参数具体如下:定子电阻Rs=2.875Ω;铜损电阻RFe=108.23Ω;直、交轴电感Ld=Lq=0.008 5 H;转子磁链Ψf=0.175 Wb;额定电压VN=380 V;额定转速nN=1 500 rad/min;转动惯量J=1.00e－3 kg·m2，极对数 nN=2。

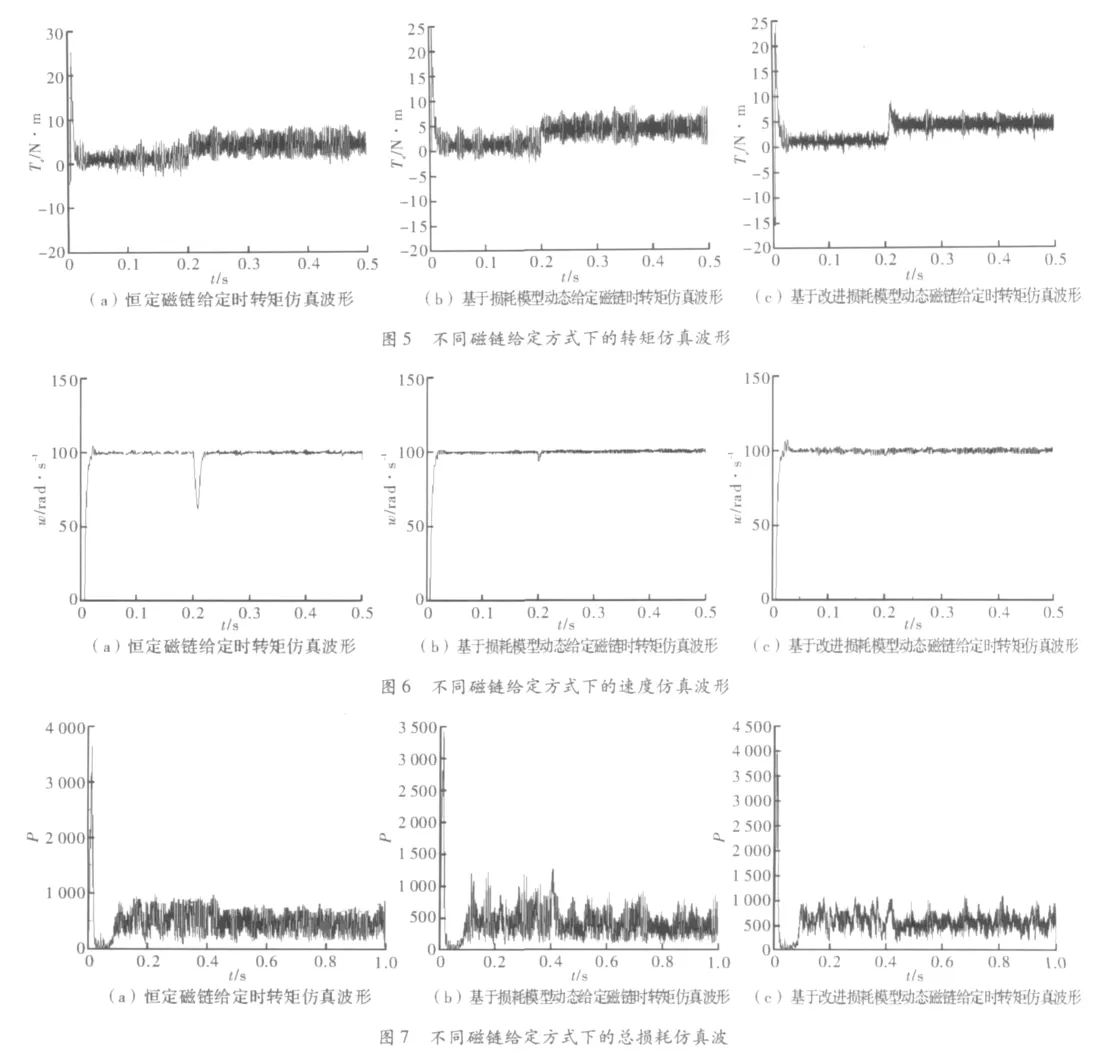
设定初始负载转矩为1 N·m，在0.2 s时变为4 N·m，转速为100 rad/s。图5和图6分别为不同给定磁链方式下转矩和速度的仿真波形。从仿真结果中可以看出，无论是在启动至平稳时，还是在转矩突变时，基于损耗模型动态给定磁链方式和基于改进的损耗模型动态给定磁链方式的响应性能都优于给定磁链方式，转矩脉动相应减小，转速响应较快。图7是不同给定磁链下的总损耗仿真波形。如图7所示，相比给定磁链方式，基于损耗模型动态给定磁链方式和基于改进的损耗模型动态给定磁链方式下的总损耗明显降低，其中，基于改进的动态给定磁链方式下总损耗更小。因此，基于改进的动态给定磁链方法在同时满足快速性和稳定性的要求下提高了驱动系统效率。

4 结束语

提出了一种基于改进的损耗模型效率优化方法，通过损耗模型计算出最优磁链方程，然后采用小波神经网络定子观测器估计出实时的定子电阻值，从而计算出精确的最优磁链值，实现电动汽车电机驱动系统效率最优控制。实验结果表明，文中提出的方法能够显著提高电机运行效率、降低系统总损耗，满足系统高响应要求。

［1］于伟光，祁新梅.基于定子磁链规划的异步电机最优效率控制［J］.电气传动，2012，12(1):14 －16，21.

［2］盛义发，喻寿益.轨道车辆用永磁同步电机系统效率优化智能集成控制研究［J］.中南大学学报:自然科学版，2010，41(6):2253 －2265.

［3］曹承志，魏光华.基于小波神经网络的定子电阻参数辨识的研究［J］.信息与控制，2004，33(6):743 －748.

［4］宋聚明，苏彦明.基于精确建模下的永磁同步电动机(PMSM)最佳效率控制研究［J］.电工电能新技术，2004，23(2):22－25.

［5］徐俊峰，冯江华.考虑损耗模型永磁同步电机直接转矩控制［J］.电力电子技术，2005，39(2):24 －25，28.

［6］CAO M T，HORI Y.Convergence improvement of efficiency optimization control of induction motor drives［J］.IEEE Transactions on Industry Applications，2001，37(6):1746 －1753.

［7］ZHONG L，RAHMAN M F，HU Y W，et al.Analysis of direct torque control in parmanent magnet synchronous motor drives［J］.IEEE Trans on PE，1997，12(3):528 －535.