合并与不合并:两个相似性聚类分析方法比较

刘新涛，刘晓光，申 琪，张书杰，杨党伟，任应党，*

(1.河南省农业科学院植物保护研究所，河南省农作物病虫害防治重点实验室，农业部华北南部作物有害生物综合治理重点实验室，郑州 450002;2.河南中医学院，郑州 450008;3郑州大学生物工程系，郑州 450001)

1901年Jaccard提出的用于生物区系比较的相似性系数计算公式［1］，由于简明、准确，迅速得到人们普遍认可，在生物学等自然科学以及社会科学的众多领域被广泛应用［2］，以相似性作为尺度的聚类分析技术(SCA)也日渐普及。由于Jaccard的公式只能计算2个地区间的相似性系数，于是“合并降阶”便成为相似性聚类分析方法中的核心技术环节，并被奉为经典。人们在大中型相似性聚类分析的运算中得不到既符合统计学逻辑，又具有地理学、生物学意义的结果时，往往只怀疑自己的基础数据欠缺，而不去质疑“合并”的合理性，只能将研究和数据束之高阁。申效诚等从创立多元相似性系数计算公式入手［3-4］，彻底摈弃层层合并的环节，创建了新的多元相似性聚类分析方法(MSCA)［5-6］，经过多类群、多地理区域的运算实验［7-11］，不仅简便省时，而且聚类能力强大合理。

为了更直接鲜明地对比SCA和MSCA由于合并与不合并所产生的差异，选用小、中、大型3组数据，分别用两种方法运算，比较聚类结果。以便为MSCA的广泛应用、为生物地理学的发展提供科学依据。

1 材料与方法

1.1 材料

所用材料均来自我们建造的中国昆虫分布数据库:山西省4638种昆虫在7个小区的分布;内蒙古自治区7766种昆虫在14个小区的分布;中国16804属昆虫在67个生态区域的分布。

1.2 方法

用Jaccard的二元相似性系数计算公式将上述材料分别制出7×7、14×14、67×67的相似性系数三角矩阵备用。

1.2.1 传统的聚类分析法(SCA)

选择相似性系数最大的两个小区首先聚类，将这两个小区的分布资料合并为一个新的小区，使参与聚类的小区降为n-1个，再用Jaccard的公式计算n-1个小区的两两相似性系数，排成n-1×n-1矩阵，重新选择相似性系数最大的两个小区予以合并，使参与聚类的小区数降为n-2个。如此反复，直至全部小区聚类完成。最后，根据聚类与合并的顺序作出支序图。

式中，SI是两个小区间的相似性系数，A、B分别是两个小区的种类数，C是两个小区的共有种类数。

1.2.2 多元相似性聚类分析法(MSCA)

选择相似性系数最大的两个小区首先聚类，但不将这两个小区的分布资料合并，而是将其视为一个“单元群”，与其它没有聚类的n-2个小区一同进入下一轮聚类分析。每轮均挑选相似性系数最大者聚类，扩大原单元群或形成新的单元群，如此反复，直到聚类完成。相似性系数采用申效诚等创立的多元相似性系数公式计算。最后作出支序图。

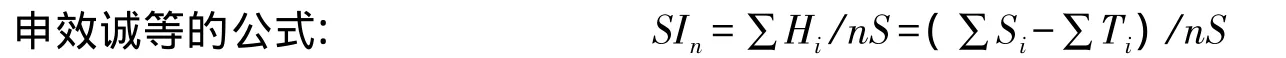
式中，SIn是要比较的n个小区间的相似性系数;Si、Hi、Ti分别是i小区的种类数、共有种类数、独有种类数，且满足Si-Ti=Hi;S为n个小区的总种类数。这些数据都可以从数据库的查询表上直接获得。

两个公式原理完全相同，前者是后者在n为2时的一个特例。后者是前者在n大于2时的通式。也即本文要比较的两个方法的区别在于合并与不合并所引起的差异。

例如表1的山西省7个小区中，5、6小区的相似性系数最大(0.412)，合并法是将其合并成一个有1413种(974+1021-582)昆虫的新小区，然后全省降为6个小区，再重新寻找相似性最大的两个小区予以合并，直到最后。

不合并法是不将5、6小区合并，而是将其视为新的聚类单元进入下一轮比较，当计算新聚类单元(包含5、6小区)与其它任一小区(1、2、3、4、7小区)间的相似性系数时，参与计算的是3个小区即n=3，在这一轮中，(5、6)和3小区间的相似性系数最大，因此，((5、6)、3)聚在一起形成了新的聚类单元;在下一轮比较时，将计算((5、6)、3)分别与1、2、4、7 小区之间的相似性系数(共4 个)，以及(1 和2)、(1 和4)、(1 和7)、(2 和4)、(2和7)、(4和7)小区间的相似性系数(共6个)，挑选其中相似性系数最大者(1和4小区)聚成一类;再下一轮比较，需要比较的聚类单元有:2小区、(1、4小区)、((5、6)、3小区)和7小区，计算相似性系数时，n值是实际参与的小区数，如计算(1、4小区)与((5、6)、3小区)之间的相似性系数时，实际参与的小区数是5个小区即n=5。依次类推，直至全部小区聚类完成。

2 结果与分析

2.1 山西省昆虫分布的聚类分析结果比较

山西省共记录4638种昆虫，其中有省下分布记录的有2619种，分布在7个小区内的种类数、共有种类数及其相似性系数如表1。

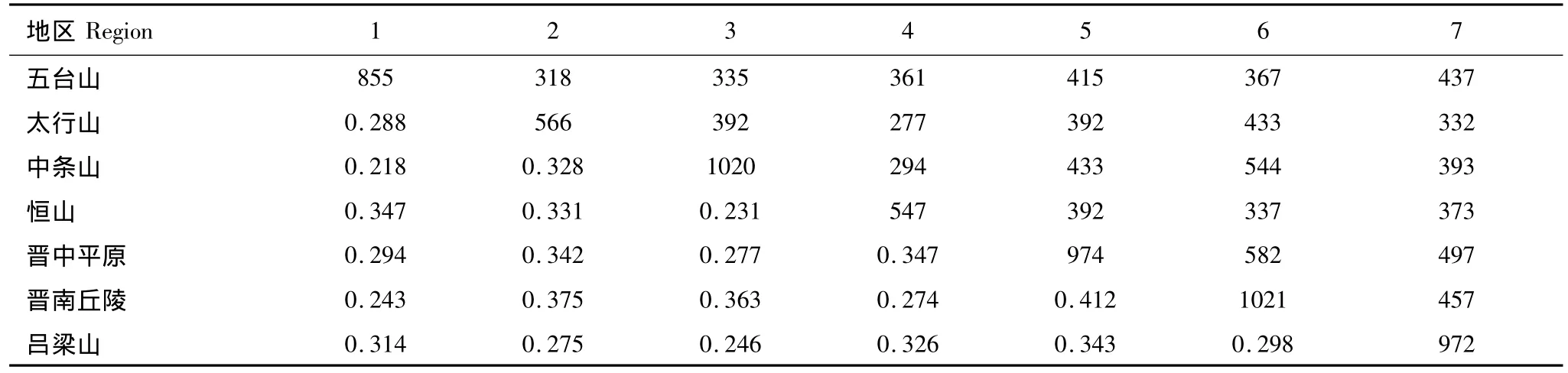
表1 山西省各地理小区的昆虫种类(对角线)、共有种类数(上三角)和相似性系数(下三角)Table 1 The insect species number(on diagonal line)，shared species number(above diagonal)and similarity coefficient(below diagonal)in every regions in Shanxi Province

使用合并法和不合并法分别得到两个聚类图(图1，图2)。

比较图1和图2，图2中7个小区在相似性系数为0.30时聚为两群。1、4、7小区聚为一群，以中低山地为主，居该省北、西方;其余4小区为一群，以平原、丘陵、低山为主，居该省中、东、南部，7个小区的总相似性系数为0.248。图1 中7 个小区起初并为3 个新小区，(1、4、7)，(2、3)，(5、6)各为一新小区。2、3 为低山，5、6则为平原丘陵，生态学意义更为突出，但它们难以以更低的相似性系数合并在一起，其生态学意义在高一级的聚类中丧失。7个小区最后的相似性系数为0.308，最多可在0.32处区分成两个新小区，同样找不到辨别3个新小区的相似性水平。两种聚类方法的结果在地理学、生物学上不存在差异，聚类结构基本没有变化。在统计上的差异:第一，相似性系数的含义不同，合并法最后的相似性系数0.308是最终合并成的山地区与平原区之间的相似性系数，必须层层合并到最后才能完成，完成时，7个小区已不复存在，支序图只是合并过程图;不合并法的相似性系数0.248确实是7个小区的总相似性系数，它不受聚类过程的影响，也不因聚类结构变动而变化，甚至可以最先计算出来;第二，合并法在2、3合并区和5、6合并区之间的相似性系数0.382比2、3合并时的系数0.328还高，这种“倒挂”现象是由合并引起的后果，致使支序图出现“凹陷”，不再是典型的梯形结构。

图1 山西省昆虫分布合并法聚类图Fig.1 The clustering graph of insect fauna of Shanxi Province by merge method

图2 山西省昆虫分布不合并法聚类支序图Fig.2 The clustering graph of insect fauna of Shanxi Province by non-merged method

2.2 内蒙古自治区昆虫分布的聚类结果比较

内蒙古自治区有昆虫7766种，有区下分布记录的共5543种。分布在14个小区的种类数、共有种类数和相似性系数如表2，两种聚类法得到两个支序图(图3，图4)。

表2 内蒙古各地理小区的昆虫种类(对角线)、共有种类数(上三角)和相似性系数(下三角)Table 2 The insect species number(on diagonal line)，shared species number(above diagonal)and similarity coefficient(below diagonal)in every regions in Inner Mongolia

图4中，在相似性系数0.20的水平上，14个小区聚为两类，一类内蒙古的东北部，以大兴安岭等山地为主要地理特征，另一类在内蒙古西南部，以高原沙漠为主要地理特征，14个小区的总相似性系数为0.159。图3中，起初12个小区分别合并为6个新小区，在以后的7次系数计算中，有3次出现了“倒挂”，而且由于合并，第9小区贺兰山和第10小区大兴安岭北段山前平原面积最小、昆虫种类最少，被排斥在外，直到最后是贺兰山和全内蒙古的比较，相似性系数为0.086，聚类结构产生较大变化，找不到一个合适的相似性水平把14个小区划分成几个有统计学和生态学意义的“类”来。“并而不类”，常常是合并法的最终结果。

图3 内蒙古昆虫分布合并法聚类图Fig.3 The clustering graph of insect fauna of Inner Mongolia by merge method

图4 内蒙古昆虫分布不合并法聚类支序图Fig.4 The clustering graph of insect fauna of Inner Mongolia by non-merged method

图4中，也出现一次“倒挂”，2、8小区之间相似性系数为0.315，3、13小区之间为0.316，但2、8、3三者的相似性系数为0.317，3小区只能放弃13小区，和2、8小区聚在一起，由于2、8没有合并，可以将3个小区并列。

2.3 中国昆虫属级分布的聚类结果比较

数据库记录到的中国昆虫共91179种，隶属于16804属，按生态条件将全国分成67个基础地理单元，对于16904属在67个单元中的分布，用两个聚类方法得到两个支序图(图5，图6)。

图6中，67个基础地理单元在相似性系数为0.25时，聚合为9群，每群所辖单元在地理上都相邻相连，在昆虫区系性质上都具有相同或相似的成分构成，可以不加任何修饰地作为我国昆虫的9个分布区。图5中，67个单元最后合并成两区，一个是由5个单元合并，包括东北的小兴安岭、三江平原，西北的阿尔泰山，和新疆南部的帕米尔高原、昆仑山，违背地理学逻辑;另一个由其余62个单元合并而成，没有生态学和生物地理学价值。66个相似性系数中，除去23个有意义的最低层次系数外，其余43个中有21个系数是倒挂的。整个过程，除是一场数字游戏外，没有出现任何有积极意义的结果。

3 结论与讨论

3.1 两种聚类方法的差异显而易见，随着比较单元的增多愈加剧烈

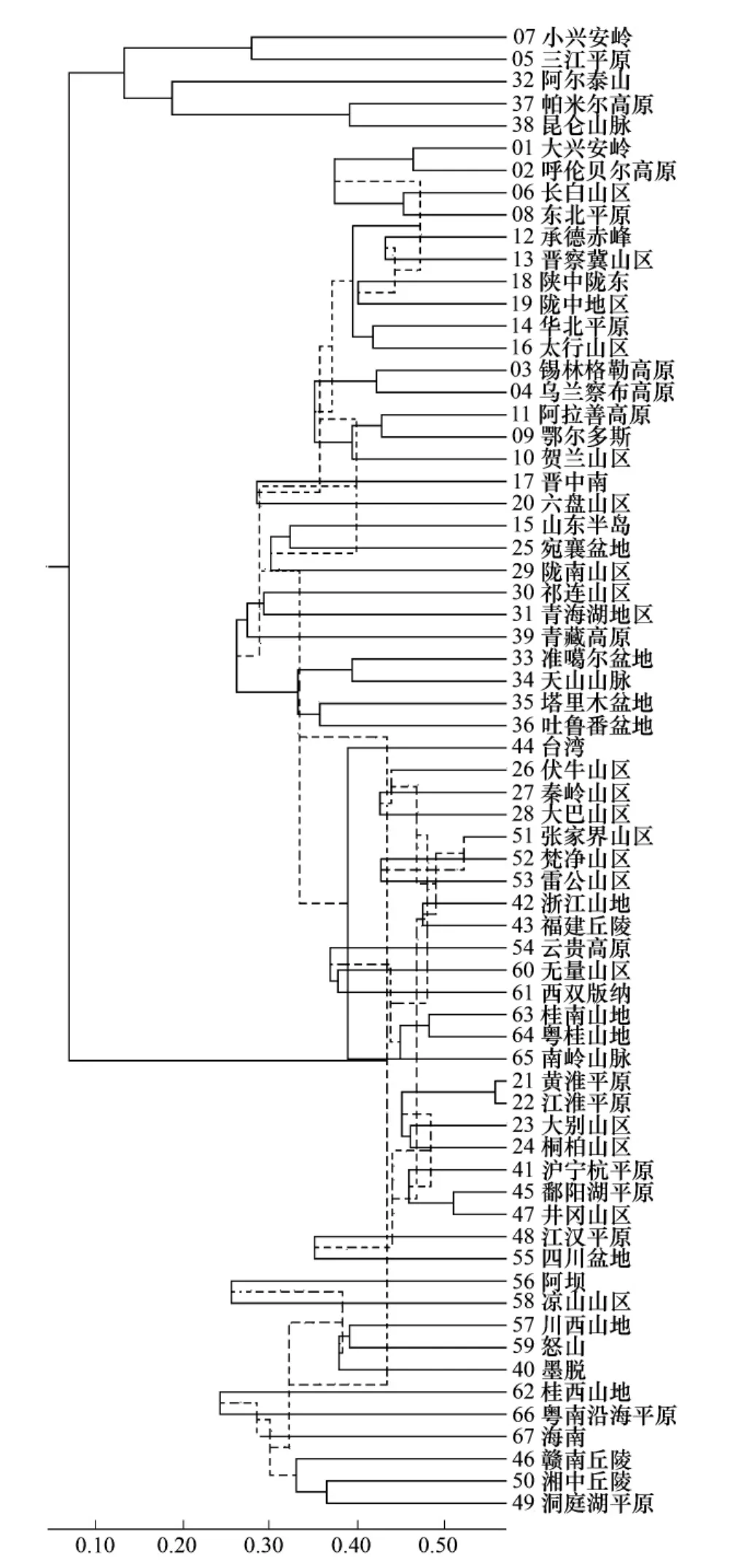
图5 中国昆虫属级分布合并法支序图Fig.5 The clustering graph of generic fauna from China by merge method

图6 中国昆虫属级分布不合并法支序图Fig.6 The clustering graph of generic fauna from China by nonmerged method

使用同一组数据，两种聚类分析方法得到不同的结果，而且随着参与比较的地理单元的增多，差异愈加剧烈，从相似性系数大小，到聚类结构变化，再到聚类功能丧失与否。这不是使用计算公式的错误，而是由于合并改变了原参与小区资料的性质所引发的变化。在参与比较的地理单元较少时(例如7个以下)，聚类结构还不至于发生不合理变动，聚类结果还有一些应用价值。参与小区达到10个以上，聚类结果则难堪相信。所以目前聚类分析的报道多是较少地理单元的应用，多地理区域、多单元参与的报告寥若晨星。这也是人们已经看到合并法的应用局限性的结果。

两种方法的计算，简便程度也差别颇大。以手工计算为例，从制成二元相似性系数表开始，到绘出支序图为止，合并法和不合并法的3个对比分别为130min和50min，4.5h和1.8h，7d和2d。合并法所浪费的时间主要在合并数据的环节。

3.2 两种聚类方法的性质迥然不同，认识须逐步到位

无论两种方法的结果差异大小，即使完全相同的情况下，其性质也决然不同。不合并法的每一个相似性系数都是所辖小区的共同的相似性关系，不受所辖小区之间的聚类顺序变动的影响;每一个系数都是独立的，它的产生没有顺序，既可从下到上，也可从上到下，又可从中间任何层次算起;所有系数都是同时存在的。所以，不合并法的支序图是一个“状态”，一个所参与地理单元在共同存在的情况下表明彼此关系亲疏、距离大小的状态。

合并法的每一个相似性系数都是有关小区经过多次合并而成的两个新小区的相似性关系，受有关小区之间的合并顺序变动的影响;每一个系数都不是独立的，它的产生遵循从下到上的顺序，前一个系数是后一个系数产生的条件，后一个系数是前一个系数消亡的结果;所有系数都不可能同时存在。所以，合并法的支序图是一个“过程”，一个所参与地理单元不断消亡新单元不断产生的过程，一个不断肯定又不断否定的过程。

相似性系数越聚越高的“倒挂”是两个方法都遇到的现象，但其性质也不相同。不合并法的倒挂是由于涉及到的3个或4个小区互相都有较高的相似性，聚类后的共同相似性系数更高的罕见现象，只出现在聚类过程中的初级层次，极少出现在较高层次，出现频次不高，出现时可以用并列法表示;合并法中的倒挂是由于合并后的两个新小区之间的较高的相似性，它主要出现在合并过程的较高层次，而且频次很高，几占较高层次的1/2。由于涉及到的小区已经合并，没有办法再把已经合并消失掉的它们并列，只能使支序图出现凹陷，失去正常的梯形结构。

3.3 合并法的历史作用值得肯定，终结其历史阶段的条件已经具备

1848年，植物学领域首先提出相似性的概念，1901年，Jaccard提出了计算两个地区间生物区系的相似性系数公式，由于其简便性、科学性，迅速得到科学界认可。此后，人们又相继提出40余个相似性公式，但都未动摇Jaccard公式的经典地位，成为多学科、多领域中相似性计算的最基础、最常用、最直观方法。由于Jaccard公式不能计算多地区的相似性系数，在相似性聚类分析中采用“合并降阶”的办法，能够在较少小区比较时得到相对满意的结果，实现了人们多区比较的愿望，使生物地理由定性研究向定量研究发展迈出了第一步，其历史性价值不容低估。随着其局限性的逐渐显现，人们曾试图对合并后的二元系数进行修饰改良［12］，但由于未脱离合并的窠臼，也难以达到预期的效果。因此在经历了短期的热情之后，众多领域的中大型聚类需求得不到满足，其积极作用便逐渐消失，以致成为制约生物地理发展的瓶颈。申效诚等人创建的多元相似性系数公式及MSCA法，彻底摈弃合并降阶这一产生偏差和错误的根源，能够得出相对客观的聚类结果，是生物地理学研究领域有效的聚类分析工具，必将使生物地理学的定量研究迈入一个新阶段。

［1］ Jaccard P.Distribution de la flore alpine dans le Bassin des Dranses et dams quelque region vasines.Bulletin de la Societe vaudoise des Sciences naturelles.Lausanne.1901，37:241-272.

［2］ Zhan Y L.Coeeficient of Similarity——An Important Parameter in Floristic Geography，Geographical Research，1998，17(4):429-434

［3］ Shen X C，Sun H，Zhao H D.A discussion about the method for multivariate similarity analysis of fauna.Acta Ecologica Sinica，2008，28(2):849-854.

［4］ Shen X C，Wang A P.A Simple Formula for Multivariate Similarity Coefficient and Its Contribution Rate in Analysis of Insect Fauna.Journal of Henan Agricultural Sciences，2008，(7):67-69.

［5］ Shen X C，Wang A P.Zhang S J.Studies on the Fauna of Noctuidae Ⅱ.Distribution and Similarity of Noctuidae in China.Acta Agriculturae Boreali-Sinica，2008，23(5):151-156.

［6］ Shen X C，Zhang S J，Ren Y D.The elements of insect fauna in China and distribution characteristics.Journal of Life Science，2009，3(7):19-25.

［7］ Zhao H D，Shen X C.A study on the Biogeography of Family Arctiidat in China//Shen X C，Zhang R Z，Ren Y D.Classification and Distribution of Insects in China，Beijing:China Agricultural Science and Technology Press，2008，381-388.

［8］ Sheng M L，Shen X C.Distribution and Multivariate Similarity Clastering Analysis of Ichneumonidae in Every Provinces，China//Shen X C，Zhang R Z，Ren Y D.Classification and Distribution of Insects in China，Beijing:China Agricultural Science and Technology Press，2008，389-393.

［9］ Shen X C，Ren Y D，Wang A P.Zhang S J.A multivariate similarity clustering analysis for geographical distribution of insects，spiders and mites in Henan Province.Acta Ecologica Sinica，2010，30(16):4416-4426.

［10］ Shen X C，Sun H，Ma X J.The multivariate similarity clustering analysis for 40，000 species of insect and spider fauna in China.Journal of Life Science，2010，4(2):35-40.

［11］ Ren Y D，Shen X C，Sun H，Ma X J.The Fauna Element and Geographical Distribution of Insect，Spider and Mite in Henan，China.Acta Agriculturae Boreali-Sinica，2011，26(1):204-209

［12］ Ward J H.Heirarchical grouping to optimize an objective function.Journal of the American Statistical Association.1963，58:236-244.

参考文献:

［2］ 张镱锂.植物区系地理研究中的重要参数——相似性系数.地理研究，1998，17(4):429-434.

［3］ 申效诚，孙浩，赵华东.昆虫区系多元相似性分析方法.生态学报，2008，28(2):849-854.

［4］ 申效诚，王爱萍.昆虫区系多元相似性的简便计算方法及其贡献率.河南农业科学，2008，(7):67-69.

［5］ 申效诚，王爱萍，张书杰.夜蛾科昆虫区系研究 Ⅱ.中国各省区夜蛾的分布及相似性分析.华北农学报，2008，23(5):151-156.

［6］ 申效诚，张书杰，任应党.中国昆虫区系成分构成及其分布特点.生命科学，2009，3(7):19-25.

［7］ 赵华东，申效诚.中国灯蛾科昆虫的生物地理学研究//申效诚，张润志，任应党.昆虫分布与分类.北京:中国农业科学技术出版社，2008，381-388.

［8］ 盛茂领，申效诚.中国各省区姬蜂科昆虫的分布及多元相似性聚类分析//申效诚，张润志，任应党.昆虫分布与分类.北京:中国农业科学技术出版社，2008，389-393.

［9］ 申效诚，任应党，王爱萍，张书杰.河南昆虫、蜘蛛、蜱螨地理分布的多元相似性聚类分析.生态学报，2010，30(16):4416-4426.

［10］ 申效诚，孙浩，马晓静.中国40000种昆虫蜘蛛区系的多元相似性聚类分析.生命科学，2010，4(2):35-40.

［11］ 任应党，申效诚，孙浩，马晓静.河南昆虫、蜘蛛、蜱螨的区系成分和分布地理研究.华北农学报，2011，26(1):204-209.