1米太阳望远镜光轴变化实测*

校启公，柳光乾，邓林华，程向明

(1. 中国科学院云南天文台光电实验室，云南 昆明 650011；2. 中国科学院研究生院，北京 100049)

为了满足天文望远镜对目标进行高时空分辨观测的要求，现代天文望远镜均配备了较灵敏的光电导行系统，导行系统的信标通常从主光学系统中引出，如云南天文台丽江天文观测站2.4 m望远镜。但也有一些特殊结构的望远镜，如云南天文台1 m太阳望远镜(New Vacumm Solar Telescope, NVST)，为改善望远镜观测时大气视宁度的状况，采用了真空镜筒，其导行系统的信标来自于独立装配在镜筒背上的导星镜[1]。独立结构的导行系统工作时，必须保证其光轴与望远镜光轴平行，但在望远镜跟踪过程中，由于受到重力的影响，支撑望远镜主副镜的镜筒或桁架会弯沉，另外导星镜机械支撑也会产生一定变化，从而影响光电导行系统的正常工作。

1 m太阳望远镜一方面对主副镜的支撑镜筒进行了等弯沉设计，另一方面采用短焦距的导星镜，加强支撑结构和镜筒刚度，导星镜镜筒最大变形控制在1″[2]。虽然该望远镜在设计上充分保证了两个光轴相对变化为最小，但望远镜最终安装运行的效果不得而知。其中，望远镜光轴的弯沉是造成光轴不平行的主要因素之一，本文从数值模拟上重点讨论，另外还对该望远镜光轴与导星镜光轴的相对变化进行了实测，分析其变化范围和规律。

1 1米太阳望远镜主体结构

1 m太阳望远镜有效口径为0.98 m，有效焦距约45 m，光学系统是修正的格里高利(Gregorian)系统，机架结构为地平式(方位-高度)装置，真空镜筒直径为1.2 m。如图1(a)，导星镜安装在望远镜镜筒背部，口镜为5 cm，焦距为38.9 cm。

图1(b)是1 m太阳望远镜光学系统图，安装在真空镜筒内，太阳光从封窗W1入射，依次经过M1、M2、M4、M3、M5、M6、M7，最后经45°镜进入高分辨成像系统。其中主镜M1是抛物面反射镜，M2和M3是椭球面反射镜，M4、M5、M6和M7是平面反射镜。望远镜在跟踪过程中，M1、M2、M4、M3、M5、M6、M7随方位转动，M1、M2、M4随高度转动。由于镜筒是M1、M2的支撑机构，在重力作用下镜筒前后两端会发生形变，主副镜M1和M2的位置及其转角都会发生变化，随着镜筒指向高度的变化，即使星像稳定在导星镜中心，在高分辨率成像系统中星像位置也会不断变化，如果承载高分辨率成像系统的光谱仪转台不进行消旋，星像变化轨迹将有径向的变化，也有轴向的变化。

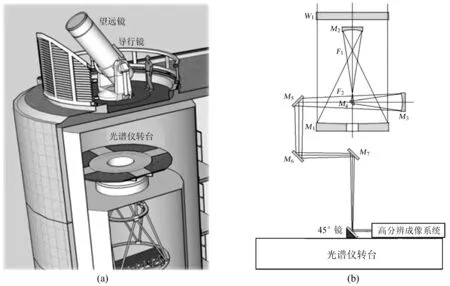
图1 1 m太阳望远镜结构及其光学系统

2 NVST主镜光轴弯沉及对跟踪精度的影响

2.1 主镜光轴弯沉的基本模型

光轴弯沉在望远镜机械设计时一般都会给予充分考虑[3]，对于1 m太阳望远镜，进行了等弯沉设计，其总体结构是：主镜采用桁架结构与中间块相连，副镜通过真空镜筒筒壁与中间块相连，这种结构使得主镜可以避免产生转角，而副镜将因真空镜筒的变形而产生转角。为了减小望远镜镜筒的变形，在镜筒内壁添加24道凹形竖筋、4圈横筋进行加强。图2(a)为1 m太阳望远镜镜筒的简化有限元模型，得到弯沉随镜筒指向高度的变化，如图2(b)，采用间隔为高度角每隔10°，然后采用最小二乘法拟合，获得了弯沉随镜筒指向高度的变化关系：

δ=7.610 5×10-6E3-0.001 4E2+0.014 4E+5.131 0

(1)

式中，δ代表弯沉；E代表望远镜的高度角。分析表明镜筒最大弯沉约5″。

图2 1 m太阳望远镜的有限元模拟及弯沉的拟合曲线

2.2 光轴弯沉引入的跟踪误差

光轴弯沉对控制系统的影响主要是引入定位跟踪误差，因此当望远镜跟踪某一颗星时，跟踪误差变化曲线就带有光轴弯沉信息。由于影响望远镜定位跟踪的误差因素众多，模拟时只考虑光轴弯沉引入的跟踪误差。根据1 m太阳望远镜的光学结构，存在光轴弯沉时，星像在平面镜M4上的轨迹随高度角的变化是一条直线，如图3。

图3中，点O表示光轴在M4上的位置，由于光轴不能准确知道，且存在初始定位误差，因此将镜筒指向高度为地平时星像的位置点设为S1，星过中天，镜筒指向天顶时星像所在点设为S2。对星进行东升西落的连续观测时，星像在直线上的运动速度就是光轴弯沉随高度的变化规律，且从点S1运动到点S2再回到S1，S1到S2之间的距离为最大光轴弯沉量。设C代表中间某一时刻星像的位置，C到光轴的距离为R，转角Ag为它与光轴O之间连线和X轴的夹角。当星像进入1 m太阳望远镜的高分辨成像系统时，由于存在像的旋转，情况会变得更为复杂。其中弯沉不但影响像的旋转半径，还会影响像的旋转角度，其中旋转半径变化R为：

图3 星像在M4的轨迹

Fig.3 The track of the image ofM4

(2)

(2)式中，假设O为坐标原点，C点的坐标为(Xc,Yc)。考虑到望远镜跟踪本身还引入像的旋转，根据文[4]，旋转角表示为：

θ=(A-π)+(E-π/2)

(3)

式中，A代表望远镜方位角；E代表望远镜高度角。除此之外还要考虑光轴弯沉引入的旋转角Ag：

Ag=tan-1(Yc/Xc)

(4)

可以得到总旋转角度为：

θF=(A-π)+(E-π/2)+Ag

(5)

因此，给定星像初始点，就可以根据光轴弯沉的变化公式(1)，以及R和θF，得到模拟星像在高分率成像系统的CCD上的运动轨迹，如图4。

图4中，(a)～(d)分别表示起点S1在第一象限、第二象限、第三象限、第四象限的星像轨迹模拟图。从模拟结果可知，光轴定不准和星的初始指向误差对观测结果的影响很大，星像变化轨迹大不相同。星过天顶时，一般光轴弯沉变化很小，这时跟踪误差曲线的变化主要是像的旋转引起，变化趋势为圆的轨迹，其圆心即光轴中心。

3 光轴相对变化的实测

3.1 实测方法

由于影响望远镜定位跟踪的误差因素众多，实测时必须采用导星镜闭环跟踪消除其他的跟踪误差因素。但这种观测模式严格来讲测得的值不是望远镜系统的光轴弯沉，而是望远镜光轴与导星镜光轴的相对变化量。考虑到导星镜本身结构的稳定性，这种相对变化量可近似表示为望远镜的弯沉，进行光电导行闭环跟踪消除其他的跟踪误差因素量。

根据1 m太阳望远镜的运行情况，选取尽量接近天顶的亮星作为观测目标，然后对该星进行闭环跟踪，时间跨度为所能观测到该星的整个夜晚，空间跨度要求主镜的镜筒指向高度从地平运动到天顶，尽量达到望远镜高度轴能工作的极限范围。然后通过1 m太阳望远镜高分辨率白光成像系统不断采集星像在CCD上的重心位置，镜筒指向高度较低时，采样间隔为高度每变化20″，星过中天前后，由于像场旋转的影响，则相应加快采样速度，采样间隔分别为高度每变化10″、5″和1″。光电导行反馈信号取自于星在导星镜CCD上的重心坐标，闭环跟踪时其跟踪误差的方位和高度角的均方根值在1″内，因此可以认为导星镜的光轴是保持不变的。

图4 不同起始位置的星像轨迹模拟

Fig.4 The simulation of the tracks of a stellar image with different starting locations

3.2 实测结果及变化规律

实测选取的目标星的赤经为14 h 16 m 15.21 s，赤纬为19°6′54.8″，实测日期是2012年3月28日，星从东边高度为11°升到天顶最大84.56°再降到西边36°。星像曝光时间为1 s，每个点取样5次，求重心并平均，最后测得星像在1 m太阳望远镜高分辨率成像系统的CCD上变化轨迹如图5。

光轴弯沉在天顶附近变化很小，星像轨迹变化主要由像场旋转引起，所以用高度角大于80°的数据点拟合圆，求得的圆心O即为理想光轴位置。各星像重心到圆心O的距离如图6，即图3中所表示的R。图6中的最小R值即图3中所表示的d。

根据不同的R和d，可以求得各星像C到图3中S2点的距离。如图7， 图7(a)是星过中天前的数据，即东边；图7(b)是星过中天后的数据，即西边。通过图7(a)采用最小二乘法拟合得到1 m太阳望远镜随镜筒指向高度的变化规律为：

δ=0.053×(0.001 2E3-0.098 4E2-12.128 5E+1 008.8)

(6)

式中，0.053是高分辨率成像系统的CCD比例尺。

拟合后的曲线如图7中实线所示，东西方向两图都很吻合，说明光轴变化只与镜筒指向高度有关，与镜筒指向的方位无关，这一点在图6中表现更清楚。镜筒指向高度从84.56°变化到11°时，望远镜光轴与导星镜的光轴相对变化量为46″。

图5 实测星像运动轨迹

Fig.5 Observed track of a stellar image

图6 光轴变化随方位角的变化关系

图7 光轴变化随高度角变化关系

Fig.7 Relation between optic axis and altitude (for the East & West sides, respectively)

对(6)式微分，还可以得到弯沉变化速率随望远镜高度角的变化关系(如图8)，分析图8得到：当镜筒指向高度由零度逐渐变大时，弯沉变化速度逐渐增大，其中镜筒指向高度在28°左右，弯沉变化最快，达到0.8 ″/°，然后变化速度又逐渐减小，到天顶基本为零。

4 小 结

望远镜光轴弯沉与其具体的结构设计、材料和制造工业等有关。本文所采用的模拟和实测方法也只是针对1 m太阳望远镜，实际测得的值是望远镜光轴相对于导星镜光轴的变化，与望远镜光轴弯沉有一定的差别，差别大小取决于导星镜机械结构的稳定性，要把这两者完全分别测出来，还有待深入研究。但对1 m太阳望远镜来讲，光电导行正是要考虑光轴的相对变化。实测的结果表明，光轴的相对变化高达46 ″，远大于理论设计的预期值，而且镜筒指向高度在28°附近时，最大变化速度为0.8 ″/° ，约10 ″/h。因此，当进行太阳光谱这类需要长时间曝光观测的目标时，光电导行闭环跟踪必须引入光轴变化改正模型，其模型可以参考本文的实测值。

图8 光轴变化速率与高度角的关系

Fig.8 Relation between optic-axis shifting speed and altitude

致谢：感谢刘忠研究员的指导和关心，同时也感谢付玉、李雪宝、郑艳芳、王瑞等在工作中给予的帮助。

[1]邓林华, 柳光乾, 程向明, 等. 1 m红外太阳望远镜光电导行系统的反馈控制分析[J]. 天文研究与技术——国家天文台台刊, 2009, 6(4): 310-318.

Deng Linhua, Liu Guangqian, Cheng Xiangming, et al. Analysis of the feedback-control system of the auto guide system of the 1m infrared solar telescope of the Yunnan Observatory[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2009, 6(4): 310-318.

[2]程向明, 陈林飞, 许骏, 等. YNST光电导行设计[J]. 天文研究与技术——国家天文台台刊, 2011, 8(2): 196-204.

Cheng Xiangming, Cheng Linfei, Xu Jun, et al. Mechanical design of the auto-guiding telescope of the YNST[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2011, 8(2): 196-204.

[3]程景全. 天文望远镜原理和设计[M]. 北京: 中国科学技术出版社, 2003.

[4]柳光乾, 付玉, 程向明. 1 m太阳望远镜光谱仪像旋转及消旋控制[J]. 天文研究与技术——国家天文台台刊, 2012, 9(1): 86-92.

Liu Guangqian, Fu Yu, Cheng Xiangming. Image-field rotation and control of counter rotation for the spectrograph of the 1m solar telescope of the Yunnan Observatory[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2012, 9(1): 86-92.

[5]张志涌. 精通MATLAB[M]. 北京: 北京航空航天大学出版社, 2001.

[6]叶修梓, 陈超祥. SolidWorks Simulation基础教程[M]. 北京: 机械工业出版社, 2009.