机器视觉高斯拟合法自动导星定心系统设计*

张 介，白金明，范玉峰

(1. 中国科学院云南天文台，云南 昆明 650011; 2. 中国科学院研究生院，北京 100049;3. 中国科学院天体结构与演化重点实验室，云南 昆明 650011)

云南天文台丽江观测站2.4 m望远镜是我国口径最大的通用型光学望远镜，其主镜直径2.4 m，望远镜的主体由液压支撑，主镜由高压气体支撑，望远镜和圆顶的驱动和各种修正及报警等由计算机全自动控制，可支持远程操作和自动操作。望远镜的成像质量好，分辨率、指向精度和跟踪精度自动化程度都较高，综合性能在国际上同级望远镜中处于中上水平。

2.4 m望远镜的开环跟踪精度达到0.5″/1.4″/2″(10/30/60 min)，启用自动导星系统时，其闭环跟踪精度可以达到0.5″(60 min)，较好地保证了云南天文台暗天体相机及分光仪(Yunnan Faint Object Spectrograph and Camera, YFOSC)、丽江地外行星探测仪(LiJiang Exoplanet Tracker, LiJET)等观测终端进行长曝光时观测数据质量。望远镜的自动导星系统采用偏置导星方式，在主光路内卡焦焦点前加入45°反射镜提取40′×40′全视场内约4′×4′区域的视场作为导星CCD的视场，然后通过跟踪导星区域内星像实现对主视场星像的跟踪，导星镜可以在与主光轴垂直的径向调整位置，一般在最外侧，不提取主视场10′×10′的视场，具有体积小、产热量低、几乎不影响镜面视宁度的优点。然而，目前的自动导星系统是制造商TTL为其早期制造的望远镜研制的，软硬件都存在一些缺陷，运行不太稳定，时常出现故障，中断望远镜的自动跟踪，影响了观测数据的质量。参考同为TTL公司的2 m级英国利物浦望远镜自动导星系统升级经验，需要升级丽江2.4 m望远镜现有自动导星系统，以进一步提高现有望远镜系统的导星精度和效率。本文针对这一需求，开发系统中的自动导星定心模块，用于后续的自动导星系统开发。

该自动导星系统首先依据望远镜观测目标及导星系统的可观测范围，从GSC哈勃导星星表查询可以用于导星的最佳星目标，接着通过移动导星反射镜位置将最佳星目标引入导星CCD视场，然后连续地从自动导星CCD获取导星图像并计算星像位置偏移量，作为控制算法的误差信号，指导望远镜的跟踪修正。由于涉及较多的功能以及硬件接口，因此选用面向对象的C++语言开发软件系统，并选用较成熟的开源软件代码库，目标开发出一套有很强拓展性的相对独立的自动导星系统。

本文主要介绍如何利用机器视觉方法从CCD图像中提取用于导星的星像及计算星像中心实际位置。第1节介绍自动导星定心系统及通用的自动导星定心算法；第2节介绍自动导星系统星像提取算法及相关参数估计方法；第3节首先介绍利用LM算法非线性最小二乘拟合对星像二维高斯拟合，计算实际星像中心位置，然后使用2.4 m望远镜的观测数据对系统进行测试，最后将高斯拟合结果与IRAF软件二维高斯拟合结果相比较；第4节说明了星像偏移量的六常数模型计算方法。

1 自动导星定心系统及定心算法介绍

自动导星定心系统工作流程如图1(a)，其软件界面如图1(b)，系统以Linux(Debian)[1]为平台，利用开源代码库WXWIDGETS[2-3]开发图形用户界面(Graphical User Interface, GUI)，CFITSIO库读写FITS文件(或SBIG相机读写驱动)，使用计算机视觉库OPENCV/LAPACK[4-5]开发星像识别算法，MATHGL[6]库生成各种图像以及LEVMAR[7]库作最小二乘拟合，算法底层为LAPACK矩阵计算，可以快速完成OPENCV和LEVMAR程序中所需矩阵运算，LAPACK有很强的拓展能力，可以实现多线程或者多台计算机的并行计算，大幅提高运算效率。系统现可以从FITS(Pence[8])文件读入数据、系统自动统计完成阈值设定、星像中心计算等。同时提供界面可以监视CCD图像，调试参数及相关结果统计显示。

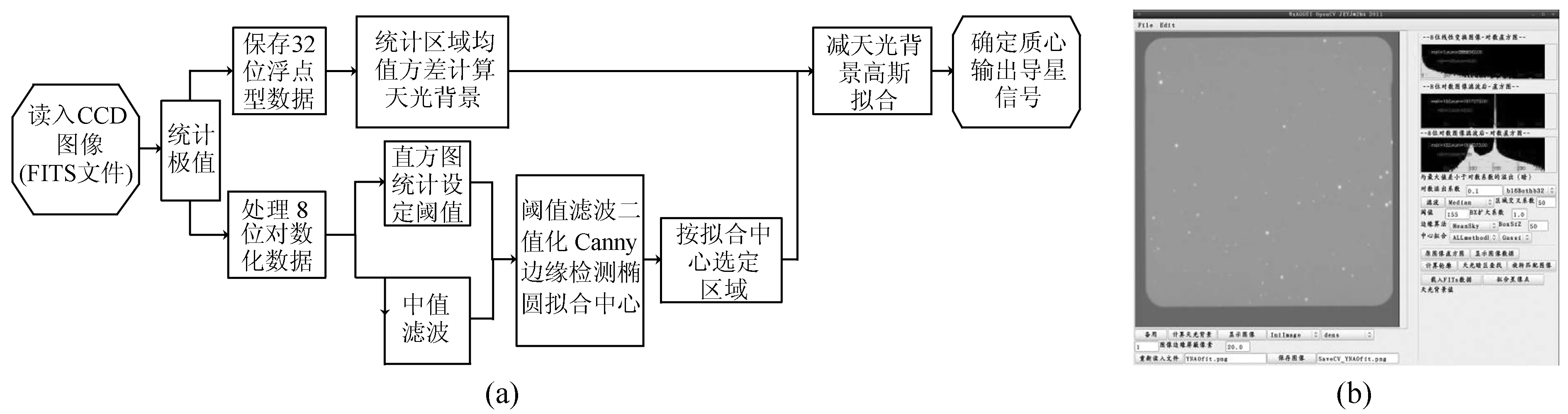
图1 自动导星系统工作流程及自动导星软件图形用户界面

Fig.1 The workflow of the auto-guiding system and the software Graphical User Interface of the system

一般的定心算法[9-14]主要有阈值一阶矩质心、平方加权质心、高斯拟合中心[15-16]及点扩散函数相关运算质心算法[17]。若定义图像中坐标(x,y)的修正灰度值为G(x,y)，则一阶矩质心为：

类似地考察图像灰度值的对称性，可以计算平方加权质心：

如果一阶矩质心与平方加权质心之间各个方向误差随机分布，说明CCD中天光背景均匀，反之需要天光背景补偿。

高斯拟合公式：

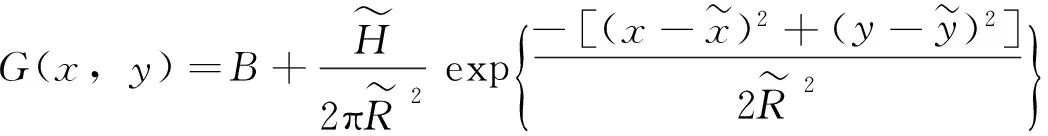
高斯拟合算法的Stone[13,18]简化公式：

高斯公式用于拟合的对数形式：

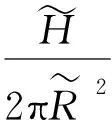
式中，B为背景天光值；P为星像最大灰度值；H对应实际星像峰值；R为拟合的高斯分布标准差。测试表明，完整模型比Stone简化模型拟合有更好的拟合精度。

此外,系统中所用椭圆拟合算法，使用OPENCV库函数效率极高，但返回结果为整型数据，有舍入误差，只能用于确定星像区域，中心位置不可靠。

2 机器视觉星像搜索算法与参数估计

OPENCV提供了一系列机器视觉处理算法，这些算法基于LAPACK矩阵计算库可以快速高效完成星像轮廓识别。针对CCD图像中星像集中的特点，首先对8位图像中值滤波去除异常噪声，接着对图像域值滤波并二值化，通过设定高于天光背景的域值可以区分星像与背景，然后可用Canny边缘[19]检测得到星像轮廓，最后再用最小二乘法拟合椭圆轮廓，估计星像区域。为简化运算及数据存贮量，使用8位对数化整数数据完成星像识别，再使用32位原数据计算星像中心位置。

2.1 Canny边缘检测、图像滤波与椭圆拟合

Canny边缘检测的算法是集低通滤波与边界检测于一体的算法，其内容如下：

第一步：利用高斯算子对图像平滑卷积滤波去除噪声，再计算图像各点的灰度变化梯度，实际OPENCV的Canny算法源程序中直接采用同时有高斯平滑和边缘检测效果的Sobel算子与原图像卷积计算，分别计算X与Y方向一阶图像差分。计算中采用3×3的模板计算。其数值如下：

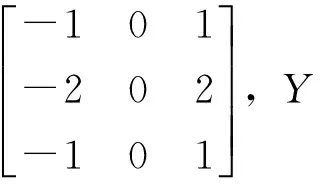
第二步：计算绝对值范数或L2范数作为梯度强度和计算梯度方向。

梯度方向θ=arctan(Dy/Dx)，其中Dy与Dx是由Sobel算法算得的Y与X方向一阶差分值。

第三步：梯度图像非极大值抑制，将非局部最大梯度值点设为零。

第四步：双阈值检测和连接边缘，沿梯度方向将图像中梯度强度大于高阈值的都存为边界点，低于高阈值且高于低阈值的梯度强度保留，再利用连通性筛选保留的梯度坐标，将与大于高阈值边界点连通的梯度强度保留，其余无效区域设为零。

对图像的滤波包括中值滤波去除异常数据点，但滤波仅对提取轮廓的8位数据进行，对用于拟合及定心计算的32位数据不进行滤波。图像Canny提取轮廓图像前利用天光背景估计值作为阈值将图像二值化，可以大幅降低Canny算法对梯度强度阈值的敏感性，程序中使用(50, 125)的阈值对可以获得比较好的效果。

然后利用轮廓提取函数可以获得相互隔离又独立连通的轮廓，最后使用最小二乘法拟合椭圆轮廓，获得星像区域。图2中测试文件为2.4 m望远镜观测数据，视场10′×10′，曝光时间30 s，JR滤波片。

图2 阈值154、160提取的星像轮廓及阈值155拟合的椭圆

Fig.2 The profiles of stellar images extracted with the threshold values 154 and 160,together with the ellipses fitted with the threshold value 155

2.2 图像灰度值直方统计与CCD图像天光背景估计

天光背景值在高斯拟合中具有很大影响，CCD图像像素直方图统计与实验表明，直方图中峰值对应灰度值为众数，可以作为天光背景值。通常可以将8位对数化灰度直方统计峰值对应灰度值加2以上值判为有效星光灰度值。

程序中考虑到众数附近的灰度值分布比较稠密，因此，在图像的不同区域叠加后只有分布在众数附近的灰度值才有可能在同子位置的值非常相近。程序首先将原数据做3×3小邻域的均值滤波，获得每个点邻域内的均值作为该点的新灰度，并将滤波结果图像边缘近1/10 CCD尺寸的区域屏蔽，接着将有效区域分为11×11不重叠的子区域，然后对相邻子区域的灰度值对应相减取绝对值，再与其他相邻子区域计算结果重叠相加，接着求取最小值所在位置作为天光背景的众数所在位置，最后将各个子区域此对应位置的灰度值相加取平均，作为天光背景值的众数估计，同时也是天光背景值估计。同理地利用均值滤波对3×3邻域标准差计算得到标准差，再求得区域叠加的最小位置，求得天光背景标准差σ(众数)估计，当然算法对星像过度稠密及天光背景不均匀的图像可能会有估计不准的问题，目前算法还未对各星像分别计算天光背景值。

图3 (a) 3×3邻域均值的区域叠加图像;(b) 3×3邻域标准差的区域叠加图像

Fig.3 (a) The image masked with a 3×3 mean-value filter;(b) The standards deviations of the masked image

为了在椭圆轮廓内限制有效区域，选择灰度值接近1/5峰值处为边界，对应于IRAF中测光孔径值，可以减小天光背景的影响，获得较好的拟合结果。

3 高斯函数拟合算法

正常星像受大气影响，图像灰度分布近似于二维高斯分布，且在各个方向应当有相同的标准差。系统采用非线性函数最小二乘拟合的方法，将参数估计问题转化为最小化目标函数问题，得到独立噪声干扰下中心位置和标准差的最大似然估计。利用Levenberg-Marquardt优化算法[9,20]拟合星像，该算法以均方误差为目标函数，兼有梯度下降和牛顿-高斯方法的下降的速度，不直接求取复杂Hessian矩阵，用Jacobi行列式估计拟Hessian矩阵，程序中采用LEVMAR开源代码作高斯最小二乘拟合。

为避免复杂的梯度函数，采用对数化数据拟合，全高斯公式Jacobi行列式为：

图4 高斯拟合结果

Fig.4 Gaussian-fitting results

图5是对2.4 m米望远镜YFOSC观测数据高斯拟合星像位置与IRAF软件高斯拟合结果比较，其最大误差不超过0.08 Pixel。拟合得到高斯分布标准差为2.5，与当时记录的视宁度为1.7″相符。

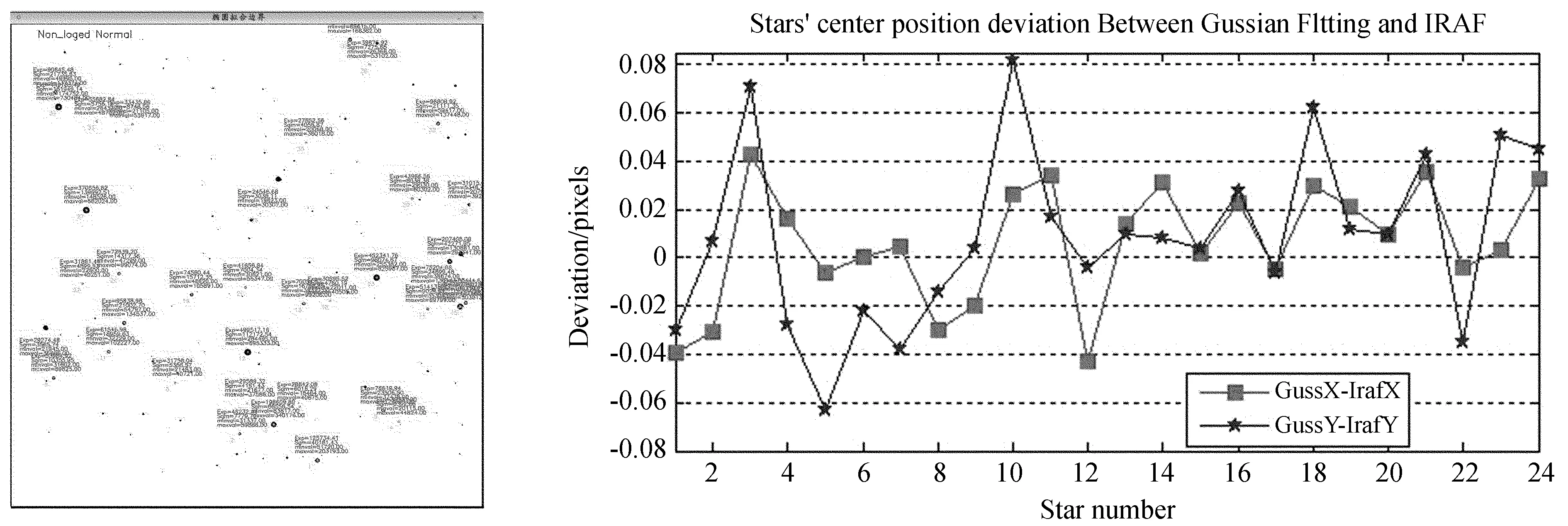
图5 丽江2.4 m望远镜数据高斯拟合结果

Fig.5 The residual errors of the stellar positions from the Gaussian fitting of the stellar profiles observed with the Lijiang 2.4m telescope of the Yunnan Observatory

4 星像偏移量计算

自动导星算法对同一天区、相邻曝光时间的两幅图像分别计算星像中心位置，并对相对应的星像计算位置偏移量，作为自动导星的误差信号。

一般认为由于相邻CCD图像间可能存在平移、旋转和缩放影响，可以用Stone[12,21-22]的算法，以六常数线性变换方程表示星像位置变换关系，如下，实际中i标识的数据量远多于变换系数个数6。

编号97图像：拍摄时间：2011-10-08T15∶02∶42.859，曝光时间30 s。

编号102图像： 拍摄时间：2011-10-08T15∶07∶20.998，曝光时间50 s。

编号105图像： 拍摄时间：2011-10-08T15∶10∶34.361，曝光时间50 s。

解六常数模型得：

abc97_102=[0.9999;2.3e-05;-0.9409]def97_102=[-8.3e-06;1.0001;2.3297]abc97_105=[1.0000;4.3e-05;-2.5640]def97_105=[2.3e-05;0.9999;3.5062]abc102_105=[1.0000;1.9e-05;-1.6231]def102_105=[3.1e-05;0.9999;1.1767]

(其中abc97_102表示97号图与102号图间X方向坐标变换系数[a102_97，b102_97，c102_97]，以此类推。)

图6为六常数模型拟合的残差，其标准化残差都小于0.06 pixel，对其残差进行Kolmogorov-Smirnov正态性检验，得到残差数据都服从0.05显著性水平的正态分布，可以认为六常数拟合已得到比较优化的结果。

图6 六常数模型97号～102号、97号～105号拟合残差

Fig.6 The residual errors of the fits with the model of six coefficients solved for the No.97 and No.102 images versus those solved for No.97 and No.105 images

5 总 结

通过自主开发的自动导星系统对导星目标的图像分析与算法实践表明，对天光背景的众数估计与直方统计的方法可以有效设定星像灰度阈值用于提取星像轮廓确定星像位置，利用基于LAPACK的LM算法可以快速高斯拟合，系统同时提供了完整的定心算法程序与参数估计方法，高斯拟合结果与IRAF软件高斯拟合结果相比较不大于0.08 pixel(YFOSC终端0.282 ″/pixel)约0.022″，可以用六常数模型计算导星误差量。而实际导星CCD像元为15 μm/pixel，对应天空角0.23 ″/pixel，可以得到更好的结果。

从算法运算效率来看，一般丽江2.4 m自动导星系统工作时导星CCD积分时间在1 s至25 s之间，而导星算法包括输出控制在毫秒量级，也就是说实际制约自动导星系统采样时间间隔的是CCD积分过程，而本算法系统虽然复杂，但即使在一般笔记本电脑(CPU T2400 1.83 GHz、内存2 G RAM、操作系统Debian6.02)，且LAPACK运算未开启多线程并行计算时，运算时间可以满足要求，另外采用导星计算与图形用户界面显示多线程运行，降低图形用户界面监控显示的频率，也可更进一步提高系统的响应速度。当然整套自动导星系统软件涉及很多方面，工程具有一定规模，需在测试和使用中进一步完善。

致谢：感谢云南天文台丽江观测站2.4 m望远镜全体工作人员，感谢王夷博同学提供的观测数据及天文数据处理方法的细致指导，感谢范绪亮同学提供的观测FITS文件。

[1]Debian operation system main page[EB/OL]. [2012-04-19]. http://www.debian.org/.

[2]Wxwidgets Main Page[EB/OL]. [2012-04-19]. http://www.wxwidgets.org/.

[3]王强, Smart J, Hock K, et al. 使用wxWidgets进行跨平台程序开发, 2006.

[4]OpenCV Main Page [EB/OL]. [2012-04-19]. http://opencv.willowgarage.com/wiki/.

[5]LAPACK Main Page[EB/OL]. [2012-04-19]. http://www.netlib.org/lapack/.

[6]MathGL-library for scientific data visualization[EB/OL]. [2012-04-19]. http://mathgl.sourceforge.net/.

[7]LEVMAR Main Page [EB/OL]. [2012-04-19]. http://www.ics.forth.gr/～lourakis/levmar/.

[8]Pence W. CFITSIO Quick Start Guide[EB/OL]. [2012-04-19]. http://stderr.org/doc/libcfitsio-doc/quick/.

[9]王海涌, 费峥红, 王新龙. 基于高斯分布的星像点精确模拟及质心计算[J]. 光学精密工程, 2009, 17(7): 1672-1677.

Wang Haiyong, Fei Zhenghong, Wang Xinlong. Precise simulation of star spots and centroid calculation based on Gaussian distribution[J]. Optics and Precision Engineering, 2009, 17(7): 1672-1677.

[10]潘波, 杨根庆, 刘勇. 星点质心定位算法最优门限研究[J]. 光学精密工程, 2008, 16(9): 1787-1792.

Pan Bo, Yang Genqing, Liu Yong. Study on optimization threshold of centroid algorithm[J]. Optics and Precision Engineering, 2008, 16(9): 1787-1792.

[11]林润芝, 杨学友, 邹剑, 等. 面向大尺寸检测CCD图像中心提取精度的研究[J]. 传感器与微系统, 2010, 29(12): 51-53.

Lin Runzhi, Yang Xueyou, Zou Jian, et al. Study on the center extraction precision of image photographed by CCD for large scale inspection[J]. Transducer and Microsystem Technologies, 2010, 29(12): 51-53.

[12]李展, 彭青玉, 韩国强. CCD图像数字定心算法的比较[J]. 天文学报, 2009, 50(3): 340-348.

Li Zhan, Peng Qingyu, Han Guoqiang. Comparison of digital centering algorithms based on CCD images[J]. Acta Astronomica Sinica, 2009, 50(3): 340-348.

[13]季凯帆, 王锋. CCD图像的二维修正矩定心方法[J]. 天文学报, 1996, 37(1): 85-90.

Ji Kaifan, Wang Feng. Two-dimensional modified moment centering algorithm in CCD images[J]. Acta Astronomica Sinica, 1996, 37(1): 85-90.

[14]季凯帆, 宋谦, 曹文达. CCD图像的一维定心方法[J]. 云南天文台台刊, 1996(4): 69-74.

Ji Kaifan, Song Qian, Cao Wenda. The one-dimention centering algorithms of CCD image[J]. Publications of the Yunnan Observatory, 1996(4): 69-74.

[15]张志渊, 彭青玉. ePSF拟合法与Gaussian拟合法的比较[J]. 天文研究与技术——国家天文台台刊, 2010, 7(2): 132-139.

Zhang Zhiyuan, Peng Qingyu. Comparison of fitting ePSF and fitting gaussian-functions[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2010, 7(2): 132-139.

[16]王娴, 苏成悦, 王婷婷. 基于有效点扩散函数的高精度测光[J]. 天文研究与技术——国家天文台台刊, 2011, 8(1): 58-63.

Wang Xian, Su Chengyue, Wang Tingting. High-precision photometry based on an effective point spread function method [J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2011, 8(1): 58-63.

[17]李春艳, 谢华, 李怀锋, 等. 高精度星敏感器星点光斑质心算法[J]. 光电工程, 2006, 33(2): 41-44.

Li Chunyan, Xie Hua, Li Huaifeng, et al. Centroiding algorithm for high-accuracy star tracker[J]. Opto-Electronic Engineering, 2006, 33(2): 41-44.

[18]Stetson P B. Photograhpic stellar photometry with the pds microdensitomter[J]. The Astronomical Journal, 1979, 84(7): 1056-1066.

[19]邓林华, 柳光亁, 黄文娟, 等. 边缘检测算子在望远镜控制系统中的应用研究[J].微计算机信息, 2010(25): 57-58.

Deng Linhua, Liu Guangqian, Huang Wenjuan, et al. Applied research of edge detection operators in telescope control system[J]. Microcomputer Information, 2010(25): 57-58.

[20]Madsen K, Nielsen H B, Tingleff O. Methods for non-linear least squares problems[M]. Informatics and Mathematical Modelling Technical University of Denmark, 2004: 58.

[21]Stone Ronald C, Monet David G, Monet Alice K, et al. The flagstaff astrometric scanning transit telescope and star positions determined in the extragalactic reference frame[J]. The Astronomical Journal, 1996, 111(4): 1721-1743.

[22]齐朝祥, 于涌, 唐正宏. 施密特巡天星表的现状和展望[J]. 天文学进展, 2008, 26(4): 349-359.

Qi Zhaoxiang, Yu Yong, Tang Zhenghong. Schmidt sky survey catalog: current status and perspectives[J]. Progress in Astronomy, 2008, 26(4): 349-359.