最大树法在登陆地域选择中的应用
2013-12-15宋剑刘永辉
宋剑 刘永辉
(海军陆战学院,广东 广州510430)
1 引言
登陆作战是一种自海上发起的对敌岸实施登陆的进攻行动,登陆地域是两栖作战部队从海上向岸上发起进攻的作战区域,包括海上(含水下)、陆上和空中三部分区域[1]。选择登陆地域时,要求充分考虑登陆部队和海、空军部队的联合作战要求。未来立体登陆作战,由于气垫艇、直升机等先进登陆装备大量运用,将对登陆地域的选择产生直接影响,除应考虑到敌情、地情等因素外,还要着眼于登陆装备的发展,选择有利于发挥现代登陆装备能力的登陆地域。
信息化作战条件下影响登陆地域选择的因素众多,指挥员单凭经验的决策方法已经不能满足实战的需要,而应在定性分析的基础上引入定量评估的方法。本文首先分析了影响登陆地域选择的主要因素,给出建模方法,建立了登陆地域分类的模型,在此基础上以第二次世界大战中著名的登陆战例——诺曼底登陆中登陆地域分类为例,进行了验证。
2 最大树法理论基础
最大树法是模糊聚类分析的一种解算方法。聚类分析的基本思想是根据对象间的相关程度进行类别的聚合,并以此来实现分类,使同一类中的个体有较大的相似性,不同类中的个体差异尽可能得大。实质就是根据研究对象本身的属性来构造模糊矩阵,在此基础上根据一定的聚类水平来确定其分类关系[2]。
2.1 建立原始数据矩阵
设论域U={x1,x2,…,xn}为n个待分类的登陆地域,每个登陆地域对象xi采用4个指标进行描述[3],即xi={xi1,xi2,xi3,xi4}={隐蔽性,机动性,易生存性,易配置性},i=1,2,…,n。
由此可以得到对各登陆地域对象进行描述的原始数据矩阵:

2.2 构造模糊相似矩阵
通过计算分类对象间的相似程度rij,可建立模糊相似矩阵R。建立模糊相似关系的方法很多,主要有数量积法、相关系数法、最大最小法、算术平均最小法、几何平均最小法、绝对值指数法、绝对值减数法、海明距离法、欧式距离法、绝对值倒数法、专家打分平均法等[4]。以上列出的11种建立模糊相似关系的方法究竟选用哪种,不能一概而论,视问题的实际情况而定,具体原则可参考相关文献。在本文的应用示例中,选用了绝对值减数法,其数学模型为:
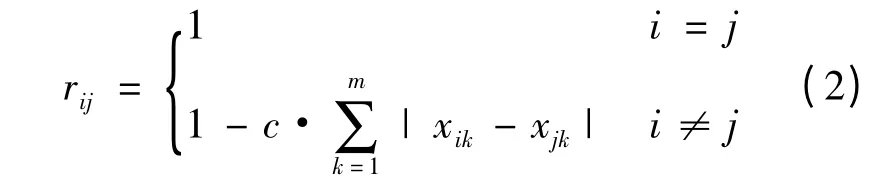
式(2)中,c为可选择的常量值。
2.3 构造最大树并分类
在模糊相似矩阵R中,按rij的大小顺序依次用直线将元素连接起来,并标上权重。若某一步出现回路,便不画这一步,直到所有元素连通为止。这样,就得到一棵所谓的最大树(可以不唯一)[6]。然后取定λ∈[0,1](聚类水平),砍断权重低于λ的枝,互相连通的元素归为一类。
2.4 分类的模糊检验
确定最佳阀值λ有两种方法[7]:一种是根据专家的经验;另一种是用F统计量确定λ。本文选用了后者来确定最佳阀值,可以避免阀值选择的主观性。

式(3)中,x¯为总体样品的中心向量,r为对应λ值的分类数,第j类的样品数为nj,第j类的样品记为,第j类的聚类中心向量=(为第k个特征的平均值,F值最大时所对应的λ即为最佳阀值。
F统计量服从自由度为(r-1,n-r)的F分布,式(3)中的分子表征类与类之间的距离,分母表征类内样本间的距离。F值越大,说明类与类之间的距离越大,表示类与类之间的差异越大,分类也就越明显。
在一定的显著性水平下,如果F>Fα(r-1,n-r),则根据数理统计方差分析原理,可以认定类与类之间的差异显著,说明在这样的显著性水平下分类是合理的。如果满足F>Fα(r-1,n-r)的分类数仍然太多,那么可以进一步减小显著性水平α,从而可以减少分类数目。
3 最大树法应用举例
回顾登陆作战的历史,因为正确选择了登陆地域而获得登陆作战胜利的例子不胜枚举,而在错误的地点进行登陆,给登陆方带来巨大损失,甚至一败涂地的例子也屡见不鲜。本文以第二次世界大战中著名的登陆战例——诺曼底登陆中登陆地域分类的问题为例进行研究。
盟军一共选择了5个登陆地点(朱诺海滩、犹他海滩、奥马哈海滩、斯沃德海滩、哥尔德海滩)。针对这5个海滩如何选择,当年组织诺曼底登陆作战的最高计划小组内部曾有过较长时间激烈的争论,但也只能凭作战经验争论优劣。
3.1 聚类计算过程
首先参照式(1)建立原始数据矩阵,记U={朱诺海滩,犹他海滩,奥马哈海滩,斯沃德海滩,哥尔德海滩}={Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ}。各登陆地域的优劣用等级{5,4,3,2,1}来对应描述{很好,好,一般,差,很差},通过相关外军资料,专家评估5个滩头的等级数据为:Ⅰ=(5,5,3,2),Ⅱ=(2,3,4,5),Ⅲ=(5,5,2,3),Ⅳ=(1,5,3,1),Ⅴ=(2,4,5,1)。
根据这五组数据,可以得到一个4×5的矩阵,其中行代表样本记录xi(i=1,2,3,4,5),列代表样本特征{xi1,xi2,xi3,xi4}。
采用绝对值减数法建立模糊相似矩阵,取c=0.1以保证rij∈[0,1],计算得模糊相似矩阵为:

取不同的λ∈[0,1],可以得到不同的分类如下:
0≤λ≤0.4时,U分为一类:U={Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ};
0.4<λ≤0.5时,U分为二类:U={Ⅰ,Ⅲ,Ⅳ,Ⅴ},{Ⅱ};
0.5<λ≤0.6时,U分为三类:U={Ⅰ,Ⅲ},{Ⅳ,Ⅴ},{Ⅱ};
0.6<λ≤0.8时,U分为四类:U={Ⅰ,Ⅲ},{Ⅱ},{Ⅳ},{Ⅴ};
0.8<λ≤1时,U分为五类:U={Ⅰ},{Ⅱ},{Ⅲ},{Ⅳ},{Ⅴ}。
经过F检验的临界参数确定,U分为三类,U={Ⅰ,Ⅲ},{Ⅱ},{Ⅳ,Ⅴ}为“效果特别显著”。
从诺曼底登陆的实际情况来看,将5个登陆地点划分为三类是最佳分类,恰好反映了各个海滩登陆兵力伤亡的轻重。第一类(伤亡程度重):朱诺海滩(伤亡1500人),奥马哈海滩(伤亡2500人);第二类(伤亡程度中等):斯沃德海滩(伤亡630人),哥尔德海滩(伤亡400人),第三类(伤亡程度轻):犹他海滩(伤亡197人)。
3.2 聚类结果分析
制定两栖作战计划时,一般要求从目标地域内初步选择数个可能的登陆地域作为备选方案。可运用上文建立的聚类分析模型计算所有备选登陆地点情况,判定各地点归为哪一类,即可判定各地点的伤亡轻重程度,从而确定选择哪个登陆点为优。参照分类结果拟定作战计划,在达到登陆胜利目的的同时,减少部队伤亡。
4 结论
本文尝试运用20世纪80年代才独立形成的模糊数学的一个点理论——聚类分析中的最大树法,对第二次世界大战中经典登陆战例——诺曼底登陆战中登陆地域分类问题,进行了回顾性的数学分析。现代数学计算结果与历史实际作战情况较好地相互吻合。事实上,最大树法不仅可以分析历史作战问题,也可在未来登陆作战中,为指挥员选择登陆地域提供参考。
1 海军兵种指挥学院.外国(地区)海军陆战队与两栖知识汇编[R].广州:海军兵种指挥学院,2011.
2 杨纶标,高英仪.模糊数学原理及应用[M].广州:华南理工大学出版社,2005.
3 伊恩,克里斯托弗.抢滩[M].张国良,谷素,译.北京:军事谊文出版社,2005.
4 李鸿吉.模糊数学基础及实用算法[M].北京:科学出版社,2005.
5 李鸿吉.Visaul Basic 6.0数理统计实用算法[M].北京:科学出版社,2003.
6 梁保松,曹殿立.模糊数学及其应用[M].北京:科学出版社,2007.
7 杨大伟.模糊聚类分析系统及其应用[J].天中学刊,2005,20(2):28-29.
