多脉波整流变压器相位测量算法

郑俊，赵刚

(上海交通大学 电气工程系，上海 200240)

0 引言

整流设备、大功率开关电源的使用日益增长，此类设备带来的大量谐波影响电网和其他设备的正常运行[1]。采用多脉波整流变压器是从源头上治理的方法[2]。只有确保多脉波整流变压器出厂测试与使用中的相位差测量的精度，才能充分发挥多脉波整流变压器的作用。

常用的过零法、波形变换法、填充计数法等相位测量方法在谐波干扰的情况下测量结果波动大、精确度低[3－4]。本文研究基于傅里叶变换相位差测量算法。

1 基于傅里叶变换的测量原理

多脉波整流变压器任意端子电压是待测信号u(t)，将u(t)按傅里叶变换得出频谱[5]，

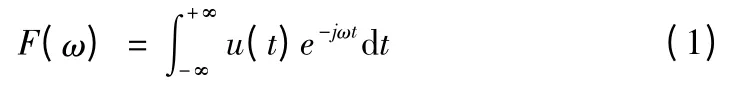
多脉波整流变压器任意两端子电压波形u1(t)，u2(t)，先做傅里叶变换得到 F1(ω)，F2(ω)，然后确定基波频率 ω0，最后计算基波相角 θ1(ω0)，θ2(ω0)，两相角相减 θ1(ω0)－ θ2(ω0)，得到任意两端子相位差。

2 提高傅里叶变换测量精度的方法

理论上，针对频率ω的傅里叶变换，其实就是对该频率对应的正弦波分量做傅里叶变换，也是对一个周期T的波形做傅里叶变换。

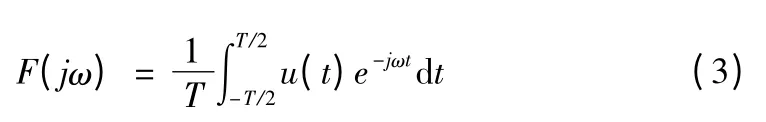
可以这样改进算法，在求得u(t)基波频率ω0后，计算基波周期，然后从采样数据中截取整周期分析数据，再做傅里叶变换计算相角。这样可以减小截断误差，提高计算精度。

3 实现与测试

用MATLAB实现了基于傅里叶变换的高精度相位差测量计算方法，全面测试该算法的计算精度。

在基波正弦波上叠加了各种高、低次谐波以及数据采集系统噪声等，模拟实际测量中不理想的电压波形作为仿真的输入测试波形，如图1所示。

全面测试相位差、低频谐波、高频谐波、基波频率、采样频率、分析数据长度、数据采集系统噪声以及算法等8个影响因素对算法准确度的影响。其中:

图1 多脉波变压器两个端子电压波形

在测试每一个影响因素时，其他变量设定为基准值保持不变，相位差15°，带有5%基波幅值的3次、5次、7次的低频谐波和5%基波幅值的11次、13次的高频谐波、基波频率50 Hz，采样频率10 kSa/s，分析数据长度10基波周期，数据采集系统噪声1%基波幅值。每种情况测试10次，计算测量误差平均值和标准偏差。

3.1 相位差

改变两输入电压波形的相位差，测试本算法测量各种相位差的精度。测试值与理论值的关系如图2所示，无谐波理想波形输入时，误差小于0.1%。波形输入对1为理想波形叠加5%基波幅值的3、5、7、11、13次谐波。波形输入对2为理想波形叠加了10%基波幅值的 3、5、9、11、15、19次谐波。测量对象相位差在 1°～15°内变化时，误差小于0.35%。常见的24、48脉波的相邻相相位差即在此范围内。

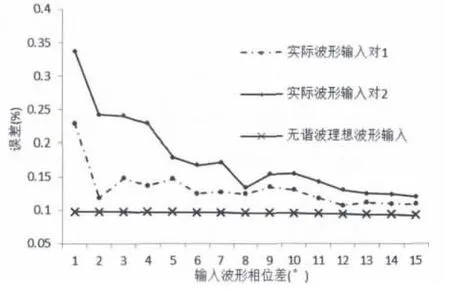
图2 不同输入对相位差对算法的影响

3.2 低频谐波

本文以9次及以下谐波为低频谐波，在正弦基波上分别叠加1%～10%基波幅值的低频谐波，测试低频谐波对该算法计算相位差的影响。步长1°，分别取1°至15°相位差，计算误差平均值及标准偏差，如表1所示。

3.3 高频谐波

本文以11次及以上谐波为高次谐波，在正弦基波上分别叠加1%～10%基波幅值的高频谐波，测试高频谐波对该算法计算相位差的影响。步长1°，分别取1°至15°相位差，计算误差平均值及标准偏差，如表2所示。

表1 低频谐波影响

表2 高频谐波影响

3.4 基波频率

实际工作中测试电源频率基频会在50 Hz附近波动，为此在47 Hz～53 Hz的变化范围内测试，评估基频变化对该算法计算相位差的的影响。如图3所示，该算法在基频扰动的情况下依然能保持很好的计算稳定性，误差低于0.5%。

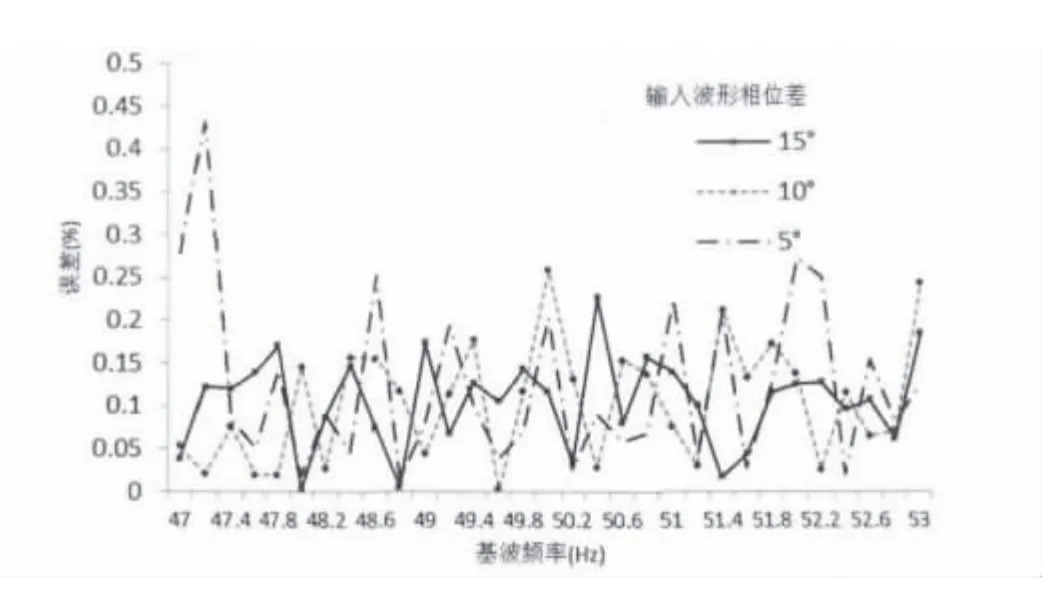
图3 基频变化对算法的影响

3.5 采样频率

对输入波形对做不同采样频率的测试，分析采样频率对该算法精度的影响。如图4所示，理论上，采样频率越高，计算越精确。当采样频率达到10 kSa/s时达到一个比较高的稳定值。实际的相位测量系统，可以根据精度的要求以及硬件的条件选择合适的采样频率。

3.6 分析数据长度

傅里叶计算的分析数据长度对算法的精确度也有影响。如图5所示，整体的趋势上，分析数据长度(积分的周期)越长(多)计算精度越高，当分析数据长度为10个周期(分析数据点数乘以采样周期Ts是10个基波周期)能达到一个比较精确的值。但分析数据长度长，计算时间也长，所以在能满足精度要求的条件下，分析数据长度越短越好。

3.7 数据采集系统噪声

数据采集系统噪声包括了分压器或电压互感器，数据采集卡(DAQ)等的热噪声。

在正弦基波上叠加0.5%、1%、2%、5%、10%基波幅值的随机噪声模拟数据采集系统噪声。观察噪声系统对算法精确度的影响。如图6所示，当噪声幅值小于2%基波幅值时，算法计算精度稳定在0.5%以内。

图6 DAQ噪声对算法的影响

3.8 算法

普通算法没有考虑基波频率变化的影响，本算法考虑了基波频率变化，计算准确积分周期，提高了基波频率变动的情况下的测量精度。两种算法误差比较见图7，当基波频率的变化，本算法有良好的精度。

图7 不同算法影响

4 结束语

傅里叶变换实际上是一种时域和频域的映射关系，能够区分各种频率分量，因此它对谐波、噪声造成的波形畸变、频率漂移以及零点漂移等都有较好的抑制作用[7]。

基于傅里叶变换的相位差测量的误差主要是傅里叶变换的截断误差。本文通过寻找频域最大幅值得到的基波频率来求得准确的积分周期，再取整周期个分析数据点进行积分计算，基本排除了截断误差的干扰。其他误差主要源于白噪声低频段对信号源实际频率的影响、计算傅里叶变换时积分的计算误差(本文采用梯形积分法)、寻找基频时的搜索步长精度等。

通过仿真测试评估证明了本文算法的精度和不确定度。与其他的测量方法比，该算法对谐波以及噪声等干扰有很好的抑制作用，当采样频率达到10 kSa/s以上时，测量精度非常高，这在硬件上也是非常容易实现的。针对多脉波整流变压器相位测量，本文提出的基于傅里叶变化的相位差测量法是一种精度高，可靠性强，且非常实用的方法。

[1]谢慧云.延边三角型移相整流变压器设计[J].变压器，2009，46(12):15－20.

[2]Sewan Choi，Ban Sup Lee，Prasad N.Enjeti.New 24 － pulse Diode Rectifier Systems for Utility Interface of High－Power AC Motor Drives[J].IEEE Transaction on Industry Applications，1997，33(2):531－541.

[3]张家生，刘扬.相位检测方法研究[J].仪器仪表学报，2003，24(S1):307－309.

[4]叶林，周弘，张洪，等.相位差的几种测量方法和测量精度分析[J].电测与仪表，2006，43(4):11－14.

[5]宗伟，李培芳，盛惠兴.信号与系统分析[M].北京:中国电力出版社，2007.

[6]李磊源，施文康.一种高可靠性的相位检测实用算法[J].上海交通大学学报，2002，36(7):987－990.

[7]庞浩，李东霞，俎云霄，等.应用FFT进行电力系统谐波分析的改进算法[J].中国电机工程学报，2003，6(23):50－54.