微重力下圆管毛细流动解析近似解研究*

李永强 张晨辉 刘玲 段俐 康琦

1)(东北大学理学院应用力学研究所,沈阳 110819)

2)(中国科学院力学研究所,国家微重力实验室,北京 100190)

(2012年9月3日收到;2012年9月8日收到修改稿)

1 引言

目前关于微重力环境下的圆管毛细流动问题受到了广泛研究,并得到了不同的液面高度对时间的依赖关系.Lucas[1]和Washburn[2]考虑了液面的毛细力和液体在水平管中的摩擦力,利用力平衡方程得到了毛细管中液面高度h随时间的变化关系为h-t1/2,并且Lucas-Washburn方程被Bell和Cameron[3]的实验所证实.由于Lucas-Washburn模型在液体流动的初始阶段假定液面速度为无穷大,因此它的有效性受到了限制,并且实验[2−5]都是在地面重力条件下用很小尺寸的管径完成的,因而在实验中观察到了液体的Lucas-Washburn行为(h-t1/2).Siegel[6]首次利用自由落体平台进行了微重力条件下的实验,微重力时间为0.74 s,在实验中观测到了液面高度随时间变化的线性阶段(h-t),但是在进入Lucas-Washburn阶段之前实验就结束了.Petrash等[7]首次利用落塔实验研究了液面高度随时间的变化,该实验中微重力时间为2.25 s,其结果也表明存在液面高度与时间呈线性关系的阶段,除此以外,他们还发现,在进入线性阶段之前,还应有一个初始的h-t2关系.有研究者尝试通过导入几种其他的影响,像惯性力[8,9]、液池自由面的曲率[7]、动态接触角[6,10,11]等来改进Lucas-Washburn方程.Levine等[12]提出了目前为止关于毛细流动的最详尽的理论.Stange等[13]利用德国不莱梅的落塔研究了微重力条件下圆柱形管中液体的毛细流动过程,从理论上建立了圆管毛细流动的非线性动力学方程,通过数值解和实验相结合的方法给出了毛细流动过程在不同阶段时毛细爬升高度随时间变化的规律.Wang等[14]研究了微重力环境下插入液体中的圆管毛细流动过程,研究了接触角和管径尺寸对毛细流动的影响,实验结果表明:随着接触角的增加,圆管中的液面高度h和液面速度˙h随着微重力时间单调的减小.随着管径尺寸的增加,在一定的微重力时间内,h-t曲线及˙h-t曲线并不是单调变化的,不同管径尺寸的h-t曲线可能相互发生交叉.

目前关于圆管毛细流动非线性动力学方程的求解尚无详尽的解析近似解研究,均采用数值解的方法.关于非线性动力学方程的解析近似求解常采用摄动法,如庞加莱-林兹斯泰德法、渐进法、多尺度法和平均法等,但这些方法对弱非线性系统是有效的,而对强非线性系统则难以应用.廖世俊[15]基于代数拓扑学中连续映射的概念,提出了一种新的求解非线性问题解析解的方法—–同伦分析法.不同于所有已知的解析近似方法,同伦分析法通过引入辅助参数和辅助函数来调节和控制级数解的收敛区域和收敛速度,该方法对强、弱非线性系统都适合,已成功解决工程技术中的许多非线性问题[16−25].

本文采用同伦分析法求解了Stange等建立的圆管毛细流动非线性动力学方程,以级数解的形式获得了内角流动的近似解析解,并给出了级数解的具体表达形式.

2 同伦分析法基本思想

Stange等[13]从理论上对微重力条件下插入液面的圆管毛细流动进行了分析,几何构型的示意图如图1所示[26].在容器内壁与圆管外壁设有防爬挡板,圆管插入液面的深度记为l0,圆管内液面中心点的位置用h表示.

图1 圆管毛细流动几何构型的示意图

初始液体高度记为l0(插入液面深度),圆管内液面高度为h,液面速度为˙h.圆管的半径为R,液面曲率的主半径为R1和R2,动态接触角为γd.容器内液体自由面的半径Rc可由防爬挡板间的距离a以及容器中自由面的中心线半径c计算得出.Stange等[13]在Levine等[12]方法的基础上做了改进,提出了毛细流动的非线性动力学方程为

其中

式中Re是雷诺数,Rex=x/ν,Red=d/ν分别是基于流动长度和流动直径d的雷诺数.一般情况下,可取K(x)≈4/3.方程(1)的边界条件为

Stange等[13]对三种介质和七种容器的圆管毛细流动进行了实验和数值分析,介质的特性参数如表1所示,容器结构参数如表2所示.其中表1中的SF 0.65和SF 1.00分别指运动黏度为0.65和1.00 cSt(1 cSt=10−4m2/s)的硅油,FC-77是含碳的氟化液系列中的一种.

表1 实验介质参数

表2 实验容器结构参数

由表 1和表 2可知,当采用 SF 1.00为实验介质和第Ⅰ号容器时,tr达到最小值,此时trmin=0.008127 s;当采用FC-77为实验介质和第Ⅶ号容器时,tr达到最大值,此时trmax=0.94024 s.当tr分别达到最大值和最小值时,s(t)的变化曲线如图2所示.

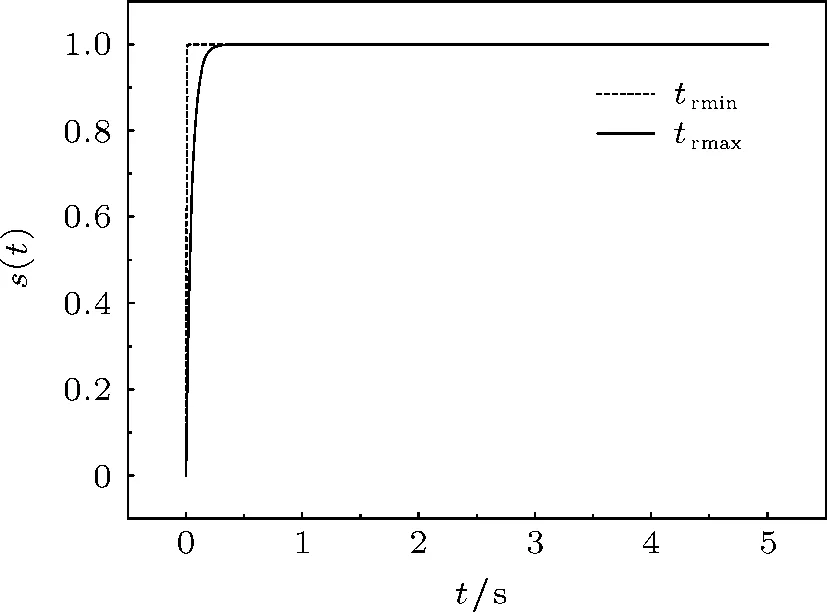
图2 s(t)-t曲线

由图2可知,s([t)≈1,故本文中设]s(t)=1.将方程(1)中的进行泰勒展开,经计算发现取前四阶即可满足计算精度,则

其中b1,b2,b3,b4和b5为展开系数,则方程(1)可简化为

其中

按照廖世俊[15]同伦分析法的基本思想,根据方程(5)的形式,定义非线性算子

其中,q∈[0,1]为嵌入变量,Φ(t;q)是未知函数h(t)的映射.设零阶形变方程为

该方程满足边界条件

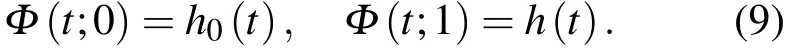
当q从0变化到1时,Φ(t;q)从初始值h0(t)变化到(5)式的解h(t).

根据(5)式,选取线性辅助算子

该线性算子具有性质

其中,C为任意常数.根据边界条件(3)式,初始值h0(t)设为

其中α为未知常数.利用泰勒展开定理,将Φ(t;q)展开成关于q的幂级数

其中

如果辅助参数¯h、辅助函数H(t)和未知常数α选取合适的值,则当q=1时,(13)式能够收敛,则可得

(15)式必定是非线性方程(5)的某一个解.定义矢量

对前面求得的零阶形变方程(7)求辅助参数q的n阶导数,再令q=0,然后除以n!,可得n阶形变方程

该方程满足边界条件

其中

根据解表达原则和系数遍历性原则[15]可以令辅助函数H(t)为

其中k为整数,研究中发现k≤2时,hn(t)中含有ln(t)项,为了避免出现ln(t)项,取

通过求解方程(17),发现hn(t)可以表达成

其中bn,j为系数,将(23)式带入到方程(16)中,按照t的次幂相等原则就可得到系数bn,j的具体表达形式.例如当n=1时,可得

系数bn,j推导的相关工作可由符号运算软件Maple或Mathmatica进行.则当级数取前m阶时,可得

式中

其中INT[]表示取整函数.

3 计算结果分析

通过上述分析可知,仅需选择合适的辅助参数α和¯h时,可确保级数解(15)式收敛.将级数解(15)式带入到方程(1)中,取平方后在区域t∈[0,5]上积分,可得平方残差为

其中

图3为初始液体高度l0=50 mm,三种实验介质在编号为Ⅶ(即R=35.0 mm)的容器内毛细流动时,液面高度取前4阶级数解时,方程(1)的平方残差E和α,¯h的关系曲线图.

图3 三种实验介质在容器Ⅶ内,液面高度前4阶级数解的平方残差Em与¯h和α的关系曲线(a)SF 0.65;(b)SF 1.00;(c)FC-77

表3 不同级数下,(24)式中系数ck的值(实验介质:FC-77,容器编号:Ⅶ,l0=50 mm)

从图3(a)可以看出,Em的最小值在α∈[0.02,0.05],¯h∈[−0.005,0.005]范围内,级数解在该区域内收敛;从图3(b)可以看出,Em的最小值在α∈[−2.5×10−4,2.5×10−4],¯h∈[0.02,0.06]范围内;从图3(c)可以看出,Em的最小值在α∈[−0.001,0.001],¯h∈[−0.01,−0.005]范围内.为了精确获得最小平方残差位置,方程(27)的极值点为

联立求解方程(29)即可得到α和¯h的值.

当实验介质为FC-77,容器编号为Ⅶ(即R=35.0 mm),初始液体高度l0=50 mm时,不同级数下(26)式中系数ck的值如表3所示.

实验介质为FC-77,容器编号为Ⅶ时,液面高度h(t)在不同时刻下的m阶同伦近似解与龙格库塔(R-K)数值计算结果的对比如表4所示.从表4可以看出,当级数m=4时,级数解就开始收敛,所以在圆管毛细流动动力学方程计算中,取级数m=4.

表4 h(t)的m阶同伦近似解与R-K数值计算结果在不同时刻的对比(实验介质:FC-77,容器编号:Ⅶ,l0=50 mm)

图4为取级数m=4时,初始液体高度l0=50 mm,三种实验介质在编号为Ⅰ(即R=2.0 mm)的容器内毛细流动时,液面高度h(t)的同伦解析近似解(HAM)与R-K数值解对比图.由图4可知,应用同伦分析法得到的解析近似解与数值法求得的解是相当符合的.

图4 h(t)的前4阶同伦解析近似解曲线

实验介质为FC-77时,(26)式中的系数ck随初始液体高度l0的变化情况如图5所示,由于系数较多,这里仅给出了c1的变化情况,其他两种实验介质的c1变化规律与FC-77相同.从图5可以看出,c1随l0和圆管半径R的增加迅速减小,当圆管半径R＞10 mm时,c1接近于零.如果实验时想要获得较高的液面高度h(t),则圆管半径不宜大于10 mm.

图5 实验介质FC-77在不同容器时,系数c1与初始液体高度l0的关系曲线

4 结论

本文应用同伦分析方法获得了微重力环境下圆管毛细流动的解析近似解并给出了级数解的表达形式.同伦分析方法为我们提供了一个方便的方法来控制渐进级数的收敛,这是同伦分析方法和其他方法根本性的区别.从同伦分析法与四阶R-K法的计算结果比较表明,同伦分析法具有较好的计算精度.

[1]Lucas V R 1918 Kolloid-Z.23 15

[2]Washburn E W 1921 Phys.Rev.17 273

[3]Bell JM,Cameron F K 1906 J.Phys.Chem.10 658

[4]Rideal E K 1922 Philos.Mag.44 1152

[5]LeGrand E J,Rense WA 1945 J.Appl.Phys.16 843

[6]Siegel R 1961 J.Appl.Mech.83 165

[7]Petrash D A,Nelson T M,Otto E W 1963 NASA TN D-1582

[8]Jeje A A 1979 J.Colloid Interf.Sci.69 420

[9]Ichikawa N,Satoda Y 1994 J.Colloid Interf.Sci.162 350

[10]Joos P,Remoortere P,Bracke M 1990 J.Colloid Interf.Sci.136 189

[11]Qu´er´e D 1997 Europhys.Lett.39 533

[12]Levine S,Reed P,Watson E J,Neale G 1976 In Colloid and Interface Science(New York:Academic)p403

[13]Stange M,Dreyer M E,Rath H J 2003 Phys.Fluids 15 2587

[14]Wang C X,Xu S H,Sun Z W,Hu WR 2009 AIAA J.11 2642

[15]Liao S J 2006 Beyond Perturbation:Introduction to the Homotopy Analysis Method(Beijing:Science Press)p204(in Chinese)[廖世俊2006超越摄动—–同伦分析方法导论(北京:科学出版社)第204页]

[16]Cheng J,Liao S J 2007 Acta Mech.Sin.39 715(in Chinese)[成均,廖世俊2007力学学报39 715]

[17]Liao S J 2003 J.Fluid Mech.488 189

[18]Li Y Q,Zhu D W,Li F 2009 Chin.J.Mech.Eng.45 37(in Chinese)[李永强,朱大巍,李锋2009机械工程学报45 37]

[19]Li Y Q,Li F,Zhu D W 2010 Compos.Struct.92 1110

[20]Yuan P X,Li Y Q 2010 Appl.Math.Mech.31 1293

[21]Li Y Q,Li L,He Y L 2011 Compos.Struct.93 360

[22]Li Y Q,Zhu D W 2011 Compos.Struct.93 880

[23]Shi Y R,Yang H J 2010 Acta Phys.Sin.59 67(in Chinese)[石玉仁,杨红娟2010物理学报59 67]

[24]Yang P,Chen Y,Li Z B 2010 Acta Phys.Sin.59 3668(in Chinese)[杨沛,陈勇,李志斌2010物理学报59 3668]

[25]Liao S J 2012 Homotopy Analysis Method for Nonlinear Differential Equations(Beijing:Higher Education Press)p285

[26]Dreyer M E 2007 Spring Tracts in Mordern Physics 221 51

[27]Sparrow E M,Lin S H,Lundgren T S 1964 Phys.Fluids 7 338