精确Cosserat弹性杆动力学的分析力学方法*

薛纭 翁德玮 陈立群

1)(上海应用技术学院机械工程学院,上海 201418)

2)(上海大学,上海市应用数学和力学研究所,上海 200072)

(2012年7月11日收到;2012年8月29日收到修改稿)

1 引言

弹性杆力学具有悠久的历史和广泛的应用背景.20世纪70年代,弹性杆被作为脱氧核糖核酸(DNA)等生物大分子的力学模型研究其位形的拓扑性质、平衡及其稳定性,进一步推动了弹性杆力学的发展[1−4].鉴于应用背景的复杂和多样性,弹性杆力学面临新的问题:其一是极端细长导致小应变累积成超大位移,形成异常复杂的几何形态;其二是全新的约束形式,如自接触等,对组蛋白的缠绕包括了经典约束具有的单面、非定常、非完整等特征[2,5].因分析力学的建模方法在约束处理和数值计算上的优势[6,7],文献[8—12]建立了Kirchhoff弹性杆静力学和动力学的分析力学理论框架,文献[13,14]将近代分析力学中的对称性理论引入弹性杆静力学,得到了由对称性导致的守恒量.

Kirchhoff弹性杆静力学和动力学的分析力学方法已有所研究,由于忽略了弹性杆截面因变形导致随弧坐标的平移,即拉压和剪切变形,使得变分原理中与主矢有关的项以及关于主矢的3个动力学方程不具有分析力学的形式,并且因主矢与主矩的耦合使得主矩方程的表达也不尽如人意[8−12],给应用带来了不便.在弯扭基础上再计及轴向拉压和截面剪切变形的弹性杆模型是Kirchhoff模型的改进[15,16],这被称之为Cosserat弹性杆或精确模型,Kirchhoff弹性杆是其特例.

本文引入了关于主矢的本构方程后形成的精确Cosserat弹性杆的分析力学方法,其变分原理和动力学方程完全具有分析力学的形式,这既有助于充分利用分析力学的现有成果为弹性杆力学提供新方法,又有利于拓展分析力学的应用领域.

精确Cosserat弹性杆运动和变形的几何关系见文献[16,17].本文基于位形空间的虚位移概念,建立弹性杆精确模型的d’Alembert-Lagrange原理和Hamilton原理,在线性本构关系下导出完全具有分析力学形式的各种运动微分方程,且以弧坐标和时间双自变量为特征.为利用分析力学的现有成果,如对称性和守恒量等以及在数值仿真时实施辛算法铺平道路.

2 弹性杆精确模型的位形描述

依据平面截面假定,以弹性杆的截面为对象,因变形导致截面随弧坐标发生转动和斜向平移,如图1所示.建立惯性坐标系(O-ξηζ)和与截面固结的形心主轴坐标系(P-xyz),沿坐标轴的单位基矢量列阵分别为和ep=(e1(t)e2(,t)e3(,t))T,其中=(s,t)为变形后的弧坐标,s为未变形时的弧坐标,e3为截面的外法矢,指向弧坐标的正向.两组基有关系ep=Q eI,Q为单位正交阵.(P-xyz)的位置和姿态用截面形心相对惯性系的矢径r=O P的坐标阵和Euler角列阵描述,r,qE的坐标依次用 qα,(α=1,···,6)表示.截面的运动方程为

图1 弹性杆截面的平移

对于给定的姿态 qα=qα(s,t),(α=4,5,6),截面随弧坐标的平移存在如下关系:∆r=e3∆s+∆w(见图 1),r(q1,q2,q3) 和 w(q1,···,q6)分别为中心线上一点P的矢径和位移矢量.于是得到关于中心线的微分方程

其中γ=∂sw为P点的应变矢量,其主轴分量γi=γ·ei,(i=1,2,3)中的前两个为截面的剪应变,第三个为拉压应变,存在关系

Kirchhoff弹性杆是取γ=0[8−12].

截面的弯扭度ω和角速度Ω为截面姿态角对弧坐标s和时间t全偏导数的线性组合

式中波浪号表示相对主轴坐标系(P-xyz)求导,ν=∂tr,ω和Ω 的Euler角表达将使(6)式成为恒等式.(2),(3),(6)和(7)式组成弹性杆精确模型的运动学方程.

值得指出的是,应变矢γ和弯扭度ω都是反映中心线弯曲的特征量.

3 弹性杆截面的虚位移

对于变形后的弹性杆,截面随弧坐标绕形心转动的同时还存在平移.定义如下弹性杆截面的虚位移[8].

定义(截面的虚位移) 约束所允许的、与弧坐标s和时间t变化无关的、假想的截面无限小位移定义为弹性杆截面的虚位移,它可分解为随形心的虚平移和相对形心的虚角位移,分别记为δr和δΦ,它对应于如下的变分定义

其中与虚位移δr和δΦ对应的广义坐标变分依次记为δpqα,(α=1,2,3)和δrqα,(α=4,5,6).对仅为广义坐标qα,(α=1,2,3)的函数的变分,有δ=δp,同理,对仅为广义坐标qα,(α=4,5,6)的函数的变分,有δ=δr.

定义微分和变分δ,δp服从交换关系

和运算的普遍性.

由(2)和(5)式知,截面的虚位移存在如下关系:

并有

与Kirchhoff模型类似,可以证明存在以下运动学关系[13]

或

以及

或

其中波浪号表示相对主轴坐标系求导或变分.这些关系也可以用Euler角验证.

若弹性杆被限制在惯性空间(O-ξηζ)中的固定光滑曲面上,约束方程为

在约束的基本假设下[8,9,11,12],(14)式可以化作对截面位形的约束方程

式中 (ξ,η,ς)为截面的形心坐标,b(s,µ(s,t))为截面与约束曲面接触点相对截面形心的矢径,bξ,bη,bζ是其投影.(15)式的变分可化为

(16)式可简写为

式中Aα为(16)式中坐标变分前的系数.方程(16)等价于理想约束条件

其中fC为曲面对杆的分布约束力集度.

4 弹性杆精确模型动力学的微分变分原理

考察原长为∆s的微段杆(图1),作用于其上的内力主矢F,主矩M,惯性力以及约束力的“虚功率”与Kirchhoff模型的区别仅在于(2)式和∂s¯s̸=1.不计因变形产生的惯性力,并利用理想约束条件,可以得到如下的“虚功率”表达式

式中ρ为弹性杆沿中心线的线密度,J为截面的惯量并矢,在主轴坐标系下的坐标阵为J=其中Ji=ρIi/A,A为截面积,I1,I2为截面对主轴x,y的惯性矩,I3为截面对主轴z的极惯性矩,且有I3=I1+I2;f(s,t)和m(s,t)为沿中心线作用的连续分布力和分布力偶.

弹性杆精确模型动力学的 d’Alembert-Lagrange原理表述为:受有理想双面约束的弹性杆在任意时刻的真实运动不同于运动学上的可能运动仅在于真实运动对于任意的虚位移,有

(19)和(20)式也可以直接从矢量形式的动力学方程导出.

设弹性杆服从线性本构关系,用主轴分量表示为

下面将用矢量表达的“虚功率”(19)式化作分析力学形式.

根据(8)—(13)式和分析力学的经典推导,对(α=1,2,3)可以导出如下关系:

式中撇号和点号分别表示∂s和∂t,Sp=为截面的平移弹性应变能和平移动能.

对(α=4,5,6)有以下关系:

以及[9]

或

可以导出

(25)和(26)式推导从略[9].(22)和(27)式的推导如下:

及

其中用到了关系

于是,(20)式化作Euler-Lagrange形式

式中,Λp=Sp−Tp,Λr=Sr−Tr,fα=f·∂r/∂qα,(α=1,2,3),fα=m·Ξα,(α=4,5,6).注意到有关系

(28)式可写成

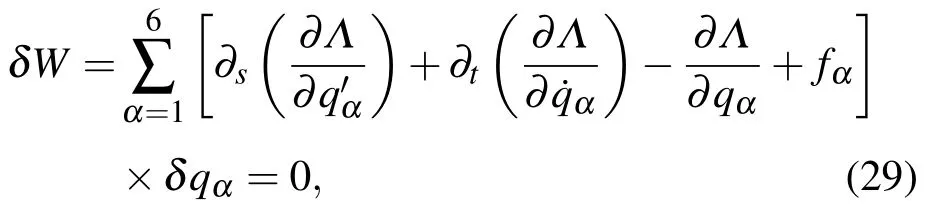
其中

为弹性杆动力学的Lagrange函数.(29)式可化作Nielsen形式

特殊地,对于除端点外不受力作用的弹性杆平衡时,动能为零,即Tp=Tr=0,由矢量形式的平衡微分方程知截面主矢F为常矢量,不失一般性,设

此守恒量不能预先嵌入上面的弹性应变能函数Sr和Sp,但可以证明存在标量函数V,使得

其中

显然,当Ki→∞时,(34)式与Kirchhoff模型一致[1]于是,(29)式化为

其中U=Sr−V.(35)式是利用守恒量(32)式的弹性杆静力学的d’Alembert-Lagrange原理.

5 弹性杆精确模型的动力学方程及其平衡问题的首次积分

对于除端点外不受约束的自由弹性杆,广义坐标变分均为独立,由原理(20),(29)和(31)式分别导出矢量形式的动力学方程

和Lagrange方程

以及Nielsen方程

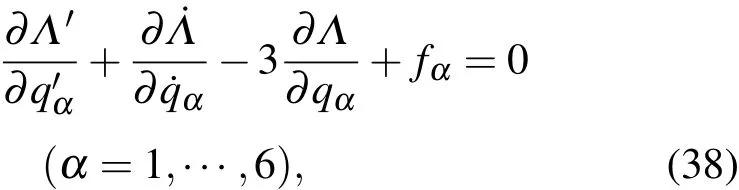
(37)和(38)式统一表达了弹性杆动力学的全部方程.对于受有形如(14)式的曲面约束,导出带乘子的Lagrange方程

从原理(35)式导出平衡微分方程

讨论(40)式的首次积分:

1)若取q1=ξ,q2=η,q3=ζ,则因∂Sp/∂qα=0(α=1,2,3),从式(40a)导出循环积分

此积分的力学意义是主矢在惯性坐标轴的分量为常量,这和平衡的矢量方程结果一致;

2)若取Euler角为姿态坐标,与Kirchhoff模型相同的是,仍有∂U/∂ψ=0,即进动角仍是循环坐标,从式(40b)导出循环积分

3)因Sp,U都不显含s,存在广义能量积分

6 弹性杆精确模型的Hamilton原理和Hamilton正则方程

将(20)式乘d s·d t后再对s和t积分,化作积分变分原理

其中用到了d-δ交换关系(9)式和端点变分条件

当弹性杆服从线性本构关系(21),且不计主动分布力f(s,t)和m(s,t)时,(44)式可进一步化作

其中Λ已由(30)式定义.(46)式就是弹性杆精确模型动力学的Hamilton原理.直接计算变分,从原理(46)式可以导出方程(37)和(38).

定义正则变量qα,以及

从而解出

定义弹性杆的Hamilton函数

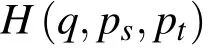
直接计算偏导数,并注意到(37)式,导出弹性杆的Hamilton正则方程

3×6 个变量 qα,psα,ptα,(α=1,···,6),(48)式共有3×6方程,方程组封闭.正则方程(48)显示了弹性杆动力学的特殊性,其相空间是3×6维.

7 结论

基于位形空间上的虚位移定义建立的精确Cosserat弹性杆动力学的d’Alembert-Lagrange原理,可以导出Lagrange方程和Nielsen方程.建立的Hamilton原理和Hamilton正则方程保持了其经典形式.从而将存在不足的Kirchhoff弹性杆动力学的分析力学方法推广到计及拉压和剪切变形情形,使弹性杆的全部动力学方程都表达成分析力学的形式,完成了分析力学方法对弹性杆动力学的移植.双自变量特征也为分析力学的进一步研究提出了新的问题.

[1]Liu Y Z 2006 Nonlinear Mechanics of Thin Elastic Rod—Theoritical Basis of Mechanical Model of DNA(Beijing:Tsinghua University Press,Springer)p1432(in Chinese)[刘延柱2006弹性细杆的非线性力学—–DNA力学模型的理论基础(北京:清华大学出版社Springer)第1432页]

[2]Liu Y Z 2003 Mech.Eng.25 1(in Chinese)[刘延柱2003力学与实践25 1]

[3]Ouyang Z C 2003 Physics 32 728(in Chinese)[欧阳钟灿2003物理32 728]

[4]Li M,Ouyang Z C 2003 Science 55 15(in Chinese)[黎明,欧阳钟灿2003科学55 15]

[5]Malacinski G M(translated by Wei Q)2005 Essentials of Molecular Biology(4th Ed.)(Bejing:Chemical Industry Press)p59(in Chinese)[乔治M马拉森斯基著(魏群译)2005分子生物学精要(北京:化学工业出版社)第59页]

[6]Westcott T P,Tobias I,Olson WK 1995 J.Phys.Chem.99 17926

[7]Pozo Coronado L M 2000 Physica D 141 248

[8]Xue Y,Liu Y Z,Chen L Q 2005 Chin.J.Theor.Appl.Mech.37 485(in Chinese)[薛纭,刘延柱,陈立群2005力学学报37 485]

[9]Xue Y,Liu Y Z 2006 Acta Phys.Sin.55 3845(in Chinese)[薛纭,刘延柱2006物理学报55 3845]

[10]Xue Y,Liu Y Z 2006 Chinese Quarterly of Mechanics 27 550(in Chinese)[薛纭,刘延柱2006力学季刊27 550]

[11]Xue Y,Wen D W 2009 Acta Phys.Sin.58 34(in Chinese)[薛纭,翁德玮2009物理学报58 34]

[12]Xue Y,Shang H L 2009 Chin.Phys.Lett.26 074501

[13]Zhao WJ,Weng Y Q,Fu JL 2007 Chin.Phys.Lett.24 2773

[14]Wang P,Xue Y,Liu Y L 2012 Chin.Phys.B 21 070203

[15]Cao D Q,Tucker R W 2008 Int.J.Solids Struct.45 460

[16]Xue Y,Weng D W,Chen L Q 2009 Chinese Quarterly of Mechanics 30 116(in Chinese)[薛纭,翁德玮,陈立群2009力学季刊30 116]

[17]Xue Y,Weng D W 2011 Mech.Eng.33 65(in Chinese)[薛纭,翁德玮2011力学与实践33 65]