公共点自动匹配算法研究

郑应新，岳建平，甄宗坤

(河海大学地球科学与工程学院，江苏南京210098)

一、引 言

三维激光扫描技术以其无接触、扫描速度快、获取信息量大、精度高、实时性强、全自动化、复杂环境测量等优点被广泛应用于测绘、逆向工程及珍贵文物保护等领域，随着应用的深入，提高点云数据处理的速度和精度的重要性也日渐突出。而点云拼接是点云数据处理的基础，也是最关键的一步，它的效率直接影响点云数据后续处理，因此，实现点云拼接的自动化具有重要的意义。目前点云拼接的方法主要有：公共点法、绝对定位法和ICP法。其中，公共点法由于其精度高、可靠性好而被广泛采用。但目前软件中自带的公共点的拼接方法多是手动或半自动的，这无疑降低了工作效率。针对这一问题，本文利用欧氏距离不变的特性提出基于重心化欧氏距离的公共点自动匹配方法，并针对该方法中可能出现的危险球问题，提出散乱点有序化自动匹配方法，以期实现拼接过程的自动化、高效化。

二、散乱点的重心化欧氏距离自动匹配

基于公共点的点云匹配方法至少需要3个公共点，在一组公共点中任意一点到该公共点组重心的距离保持不变。因此，不同测站的公共点重心认为是同名点，利用该性质可进行各公共点的匹配。

现有目标点集P、参考点集Q，两点集重心的坐标计算为

式中，n为公共点的个数。

P、Q点集中任意一点到该点集重心的距离为

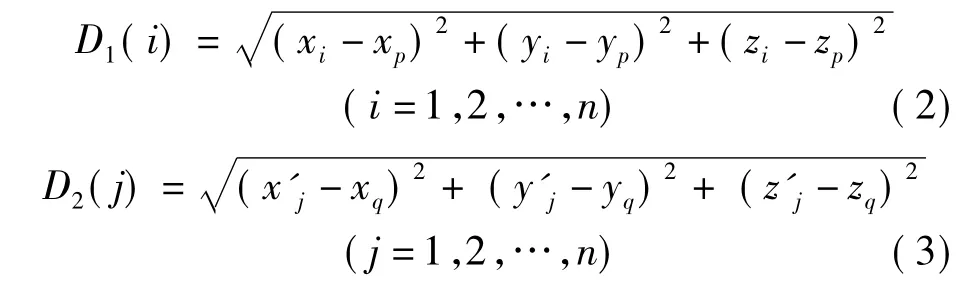
若|D1(i)－ D2(j)|＜ ε，i、j=(1，2，…，n)，则认为P中第i点与Q中第j点为对应点，据此判断其他对应点。阈值ε可根据测量精度及经验选取。

三、散乱点集有序化的自动匹配

上述方法虽然简便高效，但若有两个以上的重心化距离十分接近，将引起判断错误。为解决此问题，提出点集有序化的方法。该方法的基本思路是：计算所有公共点到重心的距离，然后选取与其他距离不相等的距离，通过不相等的距离匹配得到对应点。若不存在唯一距离，则通过角度来找稳健对应点，再计算该对稳健对应点与其他公共点的距离，并将距离排序，根据排序后的点名匹配对应点。数学模型描述如下：

重心坐标按式(1)计算，重心与公共点的距离按式(2)计算，并根据计算的距离进行判断。判断原则：若点集P中D1(i)与P中其他公共点到重心的距离的差值最大，则认为D1(i)是唯一的，在点集Q中也一定存在某段距离与其他公共点到重心的距离的差值最大，设 Q中此段距离为D2(m)，若|D1(i)－D2(m)|＜ε，则认为P中i点与Q中m点为稳健对应点。计算P中i点到其他公共点的距离，以及Q中m点到其他公共点的距离。公共点之间的距离为

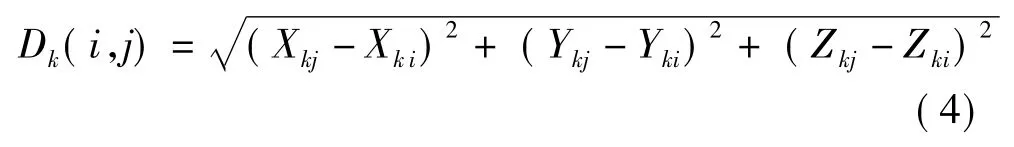
式中，i、j=1，2，…，n;k 为点集号，取值 1、2。

稳健对应点到其他公共点距离按式(4)计算完毕后，分别对两点集距离排序，即D1(i，j)＜D1(i，k)＜… ＜D1(i，n)，D2(m，h) ＜D2(m，l)＜ … ＜D2(m，n)。该不等式中，j、k表示目标点集P中点号，j、k=1，2，…，n，且 j≠k;h、l表示参考点集 Q 中的点号，h、l=1，2，…，n，且 h≠l。然后提取排序后的点号，若|D1(i，j)－D2(m，h)|＜ ε，则提取的点号自动匹配。但若稳健点到某两公共点之间距离相近，则有可能会出现匹配错误。

若点集P、Q中重心o到公共点的距离大致相等，则需通过角度来寻找最稳健的对应点。角度计算公式为

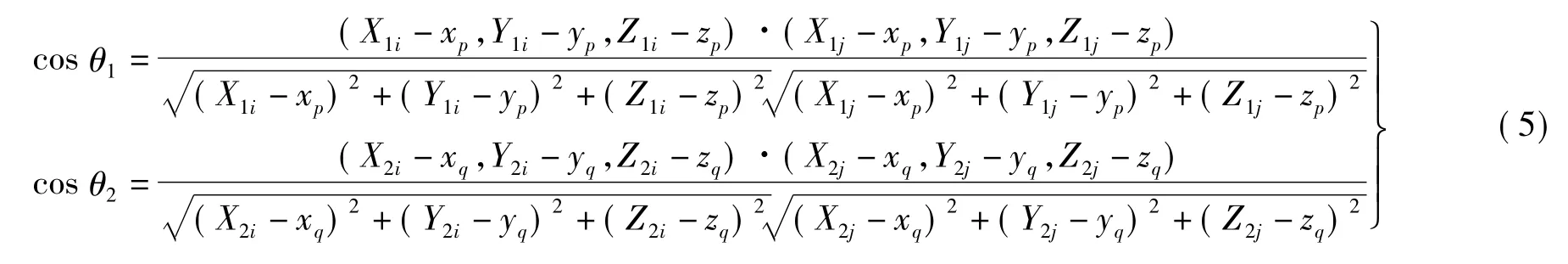
四、矢量化点集自动匹配

按下式计算以重心o为起点，各公共点为终点的向量为

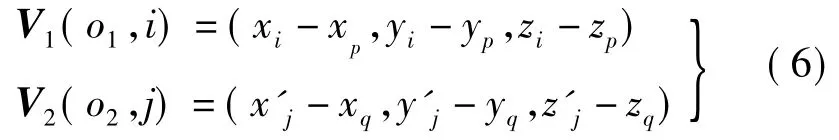
式中，(xp，yp，zp)为点集 P 的重心坐标;(xq，yq，zq)为点集 Q 的重心坐标;i、j=1，2，…，n。

向量之间夹角的计算公式为

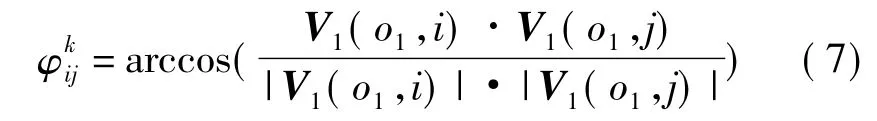
式中，k 为点集号，k=1，2;i、j=1，2，…，n。

首先判断各向量之间夹角是否相等，向量夹角的情况分为以下3种：

3)若向量夹角均相等，则在点集Q中寻找与点集P中向量长度相等的向量，进而判断匹配点。如果出现至少3个向量的长度相等，且这3个向量间夹角相等，则提示错误。

五、实例验证

对上述方法分别用实测数据进行验证，结果见表1～表3。

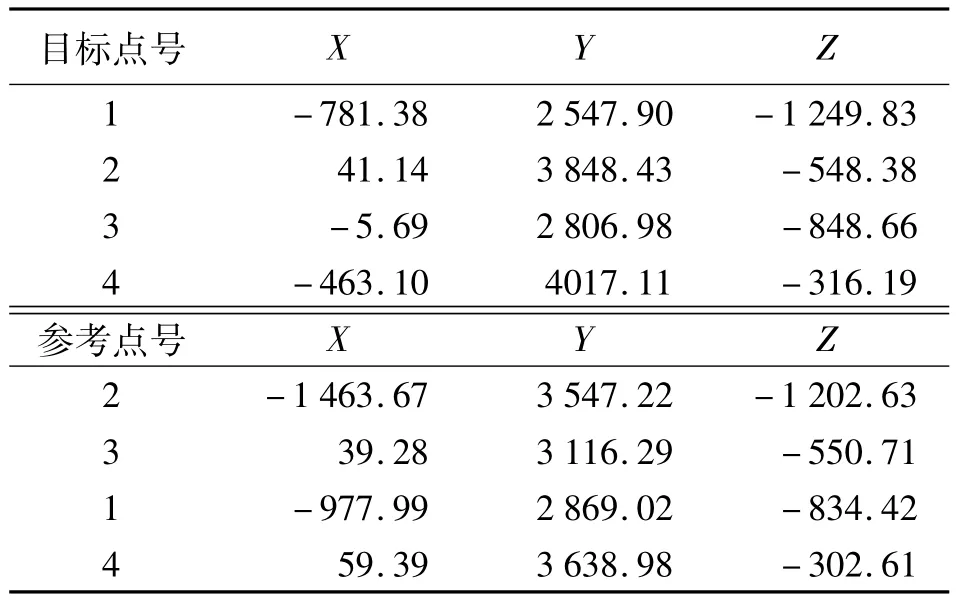
表1 散乱点重心化自动匹配结果

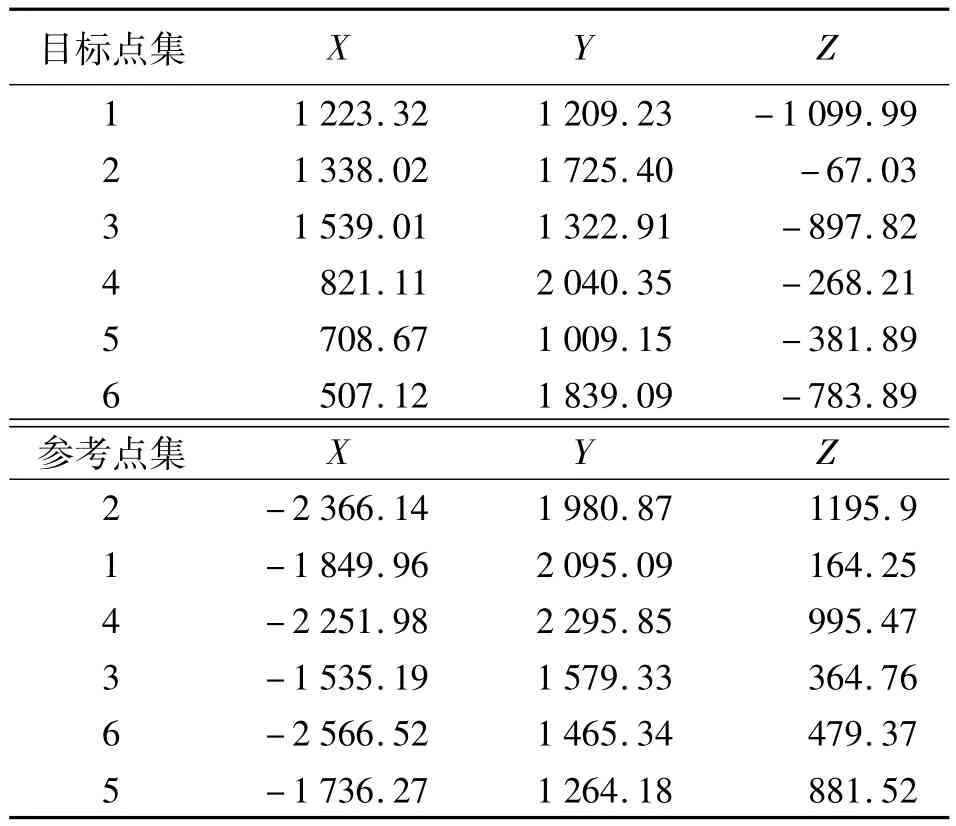
表2 散乱点有序化自动匹配结果

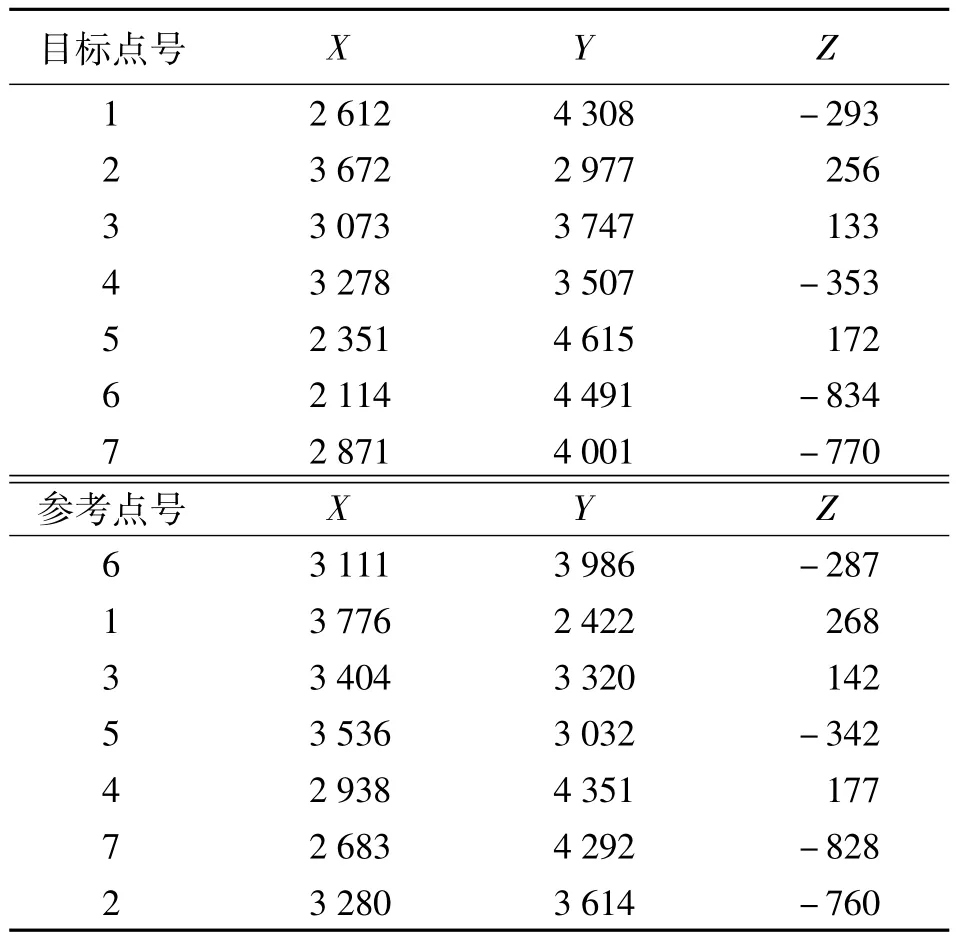
表3 矢量化方法自动匹配结果

由试验结果可以看出，3种方法匹配结果正确。通过上述方法，可快速准确地得到两站中同一标志的对应点，保证了其一一对应的关系。

六、结束语

本文研究了基于公共点自动匹配问题。结合欧氏距离不变原理提出散乱点重心化匹配方法，但如果公共点位于危险球上，上述方法可能失效，为此对该方法作了进一步改进，提出散乱点有序化的方法。试验结果表明，改进的方法可有效解决危险球问题。结合欧氏角度不变原理，提出矢量化匹配方法，并根据矢量化过程中出现的几种问题提出了相应的解决方法。从试验结果可以看出，该方法简便、高效，准确度高，可有效解决匹配过程中手动及半自动方法的问题，提高了匹配效率。

［1］王力，李广云，贺磊，等.点云拼接中标志自动匹配方法［J］.测绘科学，2011，36(2)：144-145.

［2］魏江，熊邦书，冯燕，等.基于法向量的多视点定标球球心算法［J］.计算机工程与应用，2005，41(19)：15-17.

［3］张东，黄腾，陈建华，等.基于罗德里格矩阵的三维激光扫描点云配准算法［J］.测绘科学，2012，37(1)：159-160.

［4］YANG Shen，QI Yue，SHEN Xukun，et al.Rapid and Automatic Method for 3D Scanned Data Registration［J］.Journal of Software，2010，21(6)：1438-1450.

［5］卢小平，王玉鹏，卢遥，等.齐云塔激光点云三维重建［J］.测绘通报，2011(9)：11-14.

［6］HARTLEY R，ZISSERMAN A.Multiple View Geometry in Computer Vision［M］.London：Cambridge University Press，2002.