基于最小二乘拟合的三维激光扫描点云滤波
2013-12-11严剑锋邓喀中邢正全
严剑锋,邓喀中,邢正全
(1.国土环境与灾害监测国家测绘地理信息局重点实验室,江苏徐州221116;2.中国矿业大学环境与测绘学院,江苏徐州221116)
一、引 言
地面三维激光扫描仪可快速获取扫描区域的海量三维坐标数据,在这些数据中,有进行成图、建模和分析等所需要的数据,也不可避免地存在一些影响测量结果的数据[1]。在地形扫描测量时,树木植被的遮挡及长距离和大入射角扫描引起扫描点异常的可能性较大[2-3]。点云数据滤波需要去除这些噪声点,只有将激光扫描点云数据进行滤波后,才能有效地利用扫描数据,为最终生成DEM服务。目前,点云数据滤波方法主要包括基于地形坡度的方法、基于形态学开运算方法、基于分类的算法、拟合法等[4-6]。
其中,拟合法以其原理简单、去噪效果好的优点而在地形扫描点云滤波方面得到广泛应用。传统的移动窗口曲面拟合滤波直接利用一个大尺度的移动窗口通过寻找地面最低点拟合一个粗略地形模型,然后将高差超过给定阈值的点过滤掉[7]。这种方法虽然简单,但过分依赖移动窗口的大小。本文采用基于最小二乘的拟合滤波法,将二次曲面与多面函数结合。首先使用二次曲面拟合滤波,避免了直接进行多面函数拟合错误地选取噪声点作为节点而对结果产生较大的影响;其次在二次曲面拟合去除大的噪声点基础上,再用多面函数拟合可以更好地逼近细节部分,选取准确的地形点,进而获取准确的DEM。
二、最小二乘拟合法去噪
二次曲面拟合可以总体上表达地形趋势,而多面函数拟合的基本思想是:任何一个不规则的复杂曲面均可由一系列规则的数学表面总和以任意精度逼近[8-9]。因此,多面函数可以更好地显示地形细节部分,但同时其拟合精度受节点的影响较大,这就需要保证拟合点的准确性。本文将两种拟合方法结合,首先用二次曲面拟合获取大致趋势面并去掉较大误差点,为多面函数拟合提供精度较高的可选拟合点;然后利用多面函数拟合滤波去除近地形表面的噪声点。
最小二乘曲面拟合后需要设定阈值去除噪声点,阈值的设定可根据滤波区域的地形情况及选用何种拟合方法确定。初次使用二次曲面拟合时,拟合面并不十分精确,只需去掉大的误差点,阈值适当取大,以免将非异常点去掉;第二次使用多面函数拟合去噪时,缩小阈值,去掉误差较小的噪声点,以获取精确的点云。
1.二次曲面拟合[10]
对于高程变化平缓,即在没有突变的范围内,可用曲面进行逼近代替该区域。二次曲面拟合模型为
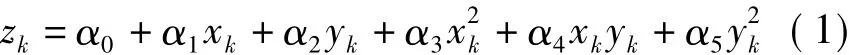
式中,(xk,yk,zk)为点的三维坐标;α0,α1,…,α5称为二次曲面拟合系数。
当拟合点数m大于必要测点数(二次曲面为6)时,有如下误差公式

用最小二乘法可求得 α0,α1,…,α5的值,从而得到二次曲面表达式。
2.多面函数拟合[9,11]
设在测区内有m个已测点S(x,y),或记为数据点(x,y,s),si为点(xi,yi)上的观测量。用 n 个核函数的总和去逼近函数S(x,y),即

式中,n为所取的已测点数,即节点数,n≤m;θ(x,y,xj,yj)为所取的核函数;α为待定系数。
核函数 θ(x,y,xj,yj)有多种类型可以选用,在测量数据处理中,一种常用的模型为具有对称性的距离型倒双曲面模型

式中,δ2为光滑因子,根据节点与拟合点的距离选用。
对于 m 个已知点 Si(xi,yi),i=1,2,…,m,方程矩阵形式为

其中,xjn、yjn表示所选的节点坐标。由最小二乘法可求得系数α的值。
三、方法原理与实现
1.点云分割
扫描得到的点云数据量庞大,不论用何种方法进行拟合去噪,都必须先选取一定数量的地表面点作为拟合点。将点云分成若干单元格,认为每个单元格中的最低点为地面点,用最低点参与拟合。
按一定的长、宽、高将点云区域分割成m×n×k个基本小单元格。郑德华[12]通过使用分割点云确定长方体单元格的方法进行直接点云精简。本文在实际的包含点云分割过程中,首先进行二维网格划分,再考虑第三维即z值的大小,以此得到需要的拟合点。具体的划分步骤包括:
1)对于二维网格的划分,为确定包含所有扫描点的长方形的大小,对于点云数据P(pi∈P),搜索P中所有点的二维方向的最大值与最小值,即xmin、xmax、ymin、ymax。则点云数据二维边界框的4个角点坐标为:(xmin,ymin)、(xmin,ymax)、(xmax,ymin)、(xmax,ymax)。
2)将覆盖整片点云的长方形区域沿x、y方向分割成m×n个小的基本长方形单元格。单元格的大小根据扫描区域及点云间隔来确定,在第一次粗略拟合去噪时一般单元格面积较大,网格边长分别为gx、gy,即

3)确定每个单元格的边界。对于每个单元格来说,需要给予相应的编号,并确定该号的单元格的边界,从而确定每个单元格内的扫描点。边界包括y方向的上界和下界、x方向的上界和下界,这样就确定了每个长方形单元格所包含的所有点。
4)搜索每个单元格内的高程最小点。扫描过程中由于遮挡或随机噪声的影响,点云分割后,不可避免地出现有些单元格为空的情况,因此人为去掉这些单元格是必要的。在剩余的单元格中逐个搜索高程最小点,得到一系列点,用于最小二乘拟合。
2.拟合去噪
用点云分割算法选取拟合点,利用上文中的方法进行两次拟合滤波。首先拟合二次曲面作为趋势面,设定较大阈值,将大噪声点去除;其次在初次滤波的基础上再选取拟合点,并从中选取部分节点,进行多面函数拟合,此时该多面函数可以很好地逼近地形表面,并精确地表达某些细节部分,去除近地表面噪声点。
四、滤波试验和结果分析
本文扫描对象为一开采沉陷区域,大小约为85 m×14 m,分别在区域两边设站扫描,中间有部分重叠。此区域产生噪声点的原因主要包括:①整片区域覆盖了大面积杂草和植被,同时有些人为堆积的土坡,如图1所示;②由于是在两边设站对中间区域扫描,因此中间部分得到的大入射角和长距离扫描点易成为噪声点;③一些随机噪声的影响。扫描共得到455 278个点。

图1 原始点云
由原始扫描点云得到该区域的DEM,如图2所示。由于噪声点分布在整个区域,因此生成的DEM效果很差,区域高低没有趋势性,与实际不符。通过该原始点云数据无法得到准确的DEM。

图2 原始点云生成的DEM
进行初次拟合滤波,通过点云单元格分割选取用于二次曲面拟合的点,本文实际选中的可用于拟合的点为1084个,得到如图3所示的二次曲面。将二次曲面与剔除掉的噪声点叠加(如图4所示),可以看出部分大的噪声点已被去除。图4中黑色长方形框中标注的扫描时的标靶,通过初次去噪已经被部分剔除。

图3 拟合的二次曲面(单位:m)

图4 二次曲面与剔除的噪声点叠加图(单位:m)
从初次滤波后的点云中再选取拟合点,并从拟合点中选取多面函数拟合节点,进行试验比较。由于拟合点较多,节点的分布对拟合的结果影响并不大,因此随机选取在整个区域上均匀分布的节点。多面函数核函数选用距离型倒双曲面模型,进行多面函数拟合滤波。经过两次去噪后,剩余的点数为291 096,滤波后的点云侧视如图5所示。和原始点云相比,植被覆盖及其他大量噪声点已经被剔除,滤波效果较为理想。

图5 滤波后的点云侧视图
由滤波后的点云生成该区域DEM,如图6所示。和图2相比,该DEM较好地表达了实际地形趋势。对滤波后准确的DEM进行三维渲染,结果如图7所示。

图6 滤波后点云生成的DEM

图7 DEM三维渲染图
对地形扫描的最终目的是建立精确的DEM及三维地形图。由上述的实例分析可见,本文的滤波方法针对不大的区域点云滤波很有效,生成的DEM及三维渲染图可以很好地反映该沉陷区的地形变化。
五、结 论
1)对于扫描得到的点云,考虑将误差分为两部分:较大误差噪声点和近地形表面噪声点。前者包含了少量粗差;后者主要是由于随机误差和低矮植被遮挡引起的。这样更有针对性地滤波可以取得较为理想的效果,进而生成准确的DEM。
2)提出点云分割算法,根据区域特点将点云区域首先进行二维划分,再考虑第三维,单元格形状和大小的选取则视扫描区域范围和地形而定,这可为两次拟合提供满足要求的拟合点。同时,由于区域长度较大,远距离处扫描点稀疏并且精度较低,若选取这些点作为拟合点,拟合出的曲面误差较大,在点云分割时可将这些点去除,用附近的较为准确点拟合的地形表面可以更好地表示该处地形。
3)传统的移动窗口最小二乘滤波只能适用于很小区域范围去噪,同时过分依赖所取窗口大小。本文在此基础上将两种拟合方法结合,利用二次曲面和多面函数的不同特点对扫描区域进行了拟合去噪,取得了较为理想的效果,为进一步两种或多种方法的组合滤波提供了借鉴。
[1]李亮,吴侃,刘虎,等.地面三维激光扫描地形测量数据粗差剔除算法及实现[J].测绘科学,2010,35(3):187-189.
[2]SOUDARISSANANE S,LINDENBERGH R,MENENTI M,et al.Scanning Geometry:Influenceing Factor on the Quality of Terrestrial Laser Scanning Points[J].ISPRS Journal of Photogrammetry and Remote Sensing,2011,66(4):389-399.
[3]张毅,闫利,杨红,等.地面激光扫描球形标靶的球心误差研究[J].武汉大学学报:信息科学版,2012,37(5):598-601.
[4]VOSSELMAN G.Slope Based Filtering of Laser Altimetry Data[J].IAPRS,2000(33):935-942.
[5]ZHANG Keqi,CHEN Shu ching,WHITMAN D,et al.A Progressive Morphological Filter for Removing Nongroud Measurements from Airborne LIDAR Data[J].IEEE Transactions on Geoscience and Remote Sensing,2003,41(4):872-882.
[6]张皓,张永生,刘军,等.一种基于平面拟合的LIDAR点云滤波方法[J].测绘科学,2009,34(4):141-143.
[7]PETZOLD B,REISSP,STOSSEL W.Laser Scaning-surveying and Mapping Agencies are Using a New Technique for the Deviation of Digital Terrain Models[J].ISPRS Journal of Photogrammetry and Remote Sensing,1999,54(2-3):95-104.
[8]吕言.数字地面模型中多面函数内插法的研究[J].武汉测绘学院学报,1981(2):14-28.
[9]王新洲,陶本藻,邱卫宁,等.高等测量平差[M].北京:测绘出版社,2006.
[10]钱锦锋.逆向工程中的点云处理[D].杭州:浙江大学,2005.
[11]张菊清,刘平芝.抗差趋势面与正交多面函数结合拟合 DEM 数据[J].测绘学报,2008,37(4):526-530.
[12]郑德华.点云数据直接缩减方法及缩减效果研究[J].测绘工程,2006,15(4):27-30.
