基于智能平面搜索的四轴机械臂避障规划

汪洋，贺小凤，郭晨

（1. 深圳信息职业技术学院 交通与环境学院，广东 深圳 518172；2. 大连海事大学信息科学技术学院，辽宁 大连 116026）

四轴机械臂是自动化加工生产中不可或缺的因素，正被广泛应用于分配、装载、包装、安放以及码垛等作业流程，涵盖了电子、汽车、塑料、食品等众多领域[1]。

随着加工工艺的复杂性与精确性不断提升，四轴机械臂在流水线上经常需要与其他工业设备协同作业，难免会出现与障碍物发生碰撞的危险，存在较大的安全隐患。因此，合理规划四轴机械臂末端的运动路径，规避工作范围内的障碍物，对于安全高效地完成作业任务便显得尤为重要。

路径规划是指给定环境的障碍物条件，以及四轴机械臂末端运动的起始点和目标点位置，要求选择一条从起始点到目标点的路径，使四轴机械臂末端能安全地规避所有的障碍物。这种自主避障并完成作业任务是四轴机械臂研究中的一个重要内容[2]。而路径规划的实质则是预先给定四轴机械臂末端作业轨迹上的关节坐标值序列，使其沿预定路径运动。

如图1所示，四轴机械臂从其底座至作业末端分别有四个自由度，依次为关节1至关节4。其中，关节1、2、4为旋转关节，关节3为滑动关节。由于关节3的纵向运动与关节4的末端带夹具运动均具有较强的灵活性，可以根据实际情况用简单的上下运动指令和旋转运动指令实时控制以规避障碍物。而关节1与关节2在水平面内的关联运动在很大程度上决定了四轴机械臂的主要位姿，两者的耦合是影响障碍物避碰的主导因素[3]。

图1 四轴机械臂Fig.1 Four-ax manipulator

所以，合理规划关节1与关节2在水平面内的关节坐标值序列，便成为四轴机械臂成功避障的关键和前提。本文即是将人工智能理论与平面几何学相结合，基于智能平面搜索提出了一种避障规划算法，用于解决四轴机械臂在X-Y平面内的二维避障问题，并加以仿真验证。

1 避障规划算法的总体思路

从俯视图投影的角度来看，工业现场的实际障碍物虽具有多种平面形状，但任何形状的障碍物投影均可被其最小外接圆包围。为简化对问题的描述又不失一般性，文中假定实际障碍物为圆柱体结构，映射到X-Y水平面上即为一圆形区域[4]。

本算法的总体思路为：先将关节1与关节2构成的关节空间q1-q2栅格化为有限个小方块，并对每个小方块编号，设定坐标值；然后根据平面几何学知识将直角坐标系X-Y下的圆形障碍区域转化为关节空间中不可达的小方块群，求出它们的编号，并给可达矩阵赋值；再采用人工智能理论中具有启发式搜索的A*算法在关节空间中求出避障路径点的编号序列；最后将该编号序列转换为对应的关节坐标值序列，关节1与关节2依次取对应的关节角度值运动即可实现对四轴机械臂的二维避障控制。

2 栅格化关节空间q1-q2

根据工业现场的实际经验，假定四轴机械臂关节1和关节2的运动范围均为[-120°,120°]，取细分精度为6°（可根据实际情况灵活选择细分精度），可将关节坐标轴q1、q2均划分为[120-(-120)]/ 6 = 40条相等的小线段，分别在每条小线段的端点作q1轴与q2轴的平行线，所有平行线相交，可将关节空间平面划分为40*40 = 1600个面积相等的小方块，从而实现了关节空间q1-q2的栅格化，如图4所示。

然后，对每个小方块进行编号并设定关节坐标值，按照从左至右、从下至上依次增大的原则，编号取[1,1600]之间的整数，在图4中，左下角小方块编号为1，右上角编号为1600，1号小方块正上方的小方块编号为41，依此类推，可得出所有小方块的唯一相异编号值。

最后，对每个小方块赋坐标值，为使坐标值分布均匀，取每个小方块的中心坐标(q1,q2)为其坐标值。则1号小方块的坐标值为(-117°,-117°)，1600号小方块的坐标值为(117°,117°)，41号小方块的坐标值为(-117°,-111°)，依此类推，可得出所有小方块的唯一相异坐标值。

3 确定障碍物所在区域

在图2中的直角坐标系下，O为坐标原点，OA2与A2B2分别为四轴机械臂的大臂与小臂。

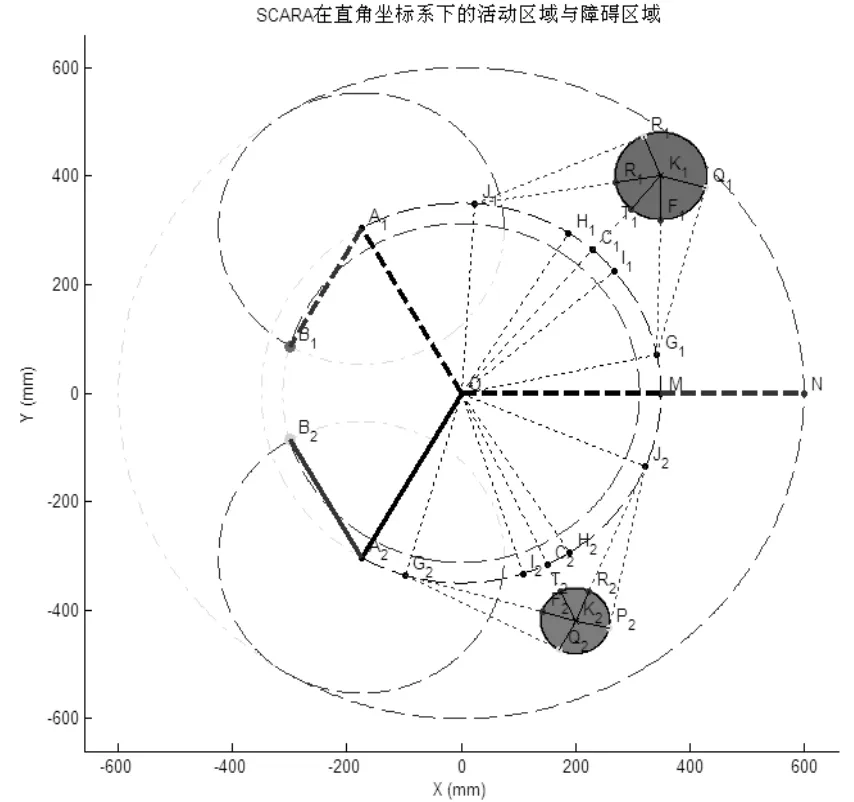
图2 四轴机械臂的工作范围与障碍物位置Fig.2 Working areas and obstacle positions of four-ax manipulator

由右手螺旋法则易知，实线OA2B2表示四轴机械臂处于关节坐标为(-117 ,-117 )的位姿，对应关节空间中的1号小方块；虚线OMN表示四轴机械臂与X轴正向重合时的位姿；虚线OA1B1则表示四轴机械臂处于关节坐标为(117 ,117 )的位姿，对应关节空间中的1600号小方块。图中蓝色与黑色虚线包围的空间即为四轴机械臂的活动区域，在该区域内假设存在两个圆形障碍物圆K1与圆K2，两圆半径均已知。由于本算法要求在关节坐标系下规划避障路径，所以要先将直角坐标系下的障碍区域转换为关节坐标系下对应的编号群。

由平面几何学知识可知，当大臂处于OG1与OJ1之间时，小臂可能与圆K1发生碰撞。仅考虑右手关节坐标系时，这一区间内的任一q1值均有两个q2值：q20与q21与之对应。其中q20为碰撞开始时的关节2角度，q21为碰撞结束时的关节2角度。两者相差为类似于角Q1G1F1的两倍的某个角度值。采用几何学方法，设位姿OG1F1为小臂末端与圆K1发生碰撞的一个极限状态，而OG1Q1为小臂延长线与圆K1相切时的位姿，切点为Q1。由图中所示的几何关系，可求出角Q1G1F1的角度值，同时在q20的基础上加上两倍的Q1G1F1的角度值，即为q21。

左手关节坐标系下的情况完全相似，不再骜述。据此可求出在q1在可能碰撞区间内的每个q2的最大最小值，从而确定障碍物K1在关节空间中的边界值。

同法也可求出圆形障碍物K2在关节空间中的边界值。

根据连通性原理，直角坐标中连通闭合的圆形区域在关节空间中必然也是连通闭合的区域[5]。只要将求出的边界值连接起来，闭合的范围就是关节坐标系下的障碍区域，而这些区域覆盖到的小方块群即为圆形障碍区域映射到关节空间内的障碍区域。

在算法中需设定一个可达矩阵，其维数为1600*1600，各元素取0或1，0表示两个小方块之间不可达，1表示可达。将障碍区域编号群中的每个编号值在可达矩阵中对应的行和列均取为0。同时为了保证每个小方块只能与其紧邻的八个小方块相通（关节空间四角的小方块只与其紧邻的三个小方块相通，四边的小方块只与其紧邻的五个小方块相通），而不出现跳步，还应在可达矩阵的相应位置赋0值。

4 搜索避障路径编号序列

在关节空间中搜索避障路径是本算法的根本所在，而搜索方式又具有决定性影响，本算法中采用A*算法实现搜索[6]。

A*算法是人工智能理论中一种典型的启发式搜索算法，在实时系统、智能控制等方面应用较广，其智能性主要体现在仅需已知起始点S、目标点G的编号与障碍区域的编号群，无需外部条件与人为判断即可实现最优避障路径的自动搜索。

本算法中先建立两个表OpenList与ClosedList，分别存放搜索过程中已生成而未扩展的小方块编号与扩展后的小方块编号；再定义估价函数 f(n) = g(n)+ h(n) 用于决定搜索方向和扩展对象，其中g(n)表示起始点S与当前小方块N之间的关节坐标距离，h(n)表示当前小方块N与目标点G之间的距离；在每一步搜索时取对应f(n)值最小的小方块进行扩展，并将该路径的编号依次存放在表ClosedList中；当搜索到的当前小方块N的编号等于目标点G的编号时结束搜索；最后将ClosedList中的编号回溯即为所求的避障路径编号序列。

5 确定避障路径关节坐标值序列

由关节空间栅格化过程可知，小方块编号值与关节坐标值是唯一对应的，求出避障路径编号序列后，只需将编号依次与关节坐标对应，即可求出最终的避障路径关节坐标值序列。当四轴机械臂的关节1和关节2依次取该序列中的每一个坐标值运动时，反映在直角坐标系X-Y下即为从起始位姿到目标位姿的二维智能避障全过程。

6 仿真验证实例

本文以深圳市众为兴技术股份有限公司自主研发的四轴机械臂SCARA为例（如图1所示），进行仿真验证。

SCARA的大臂、小臂长度分别为350mm、250mm，关节1和关节2的取值范围及空间划分参照2.1小节中的数据，设关节空间中的起始点S为1号小方块，目标点G为1600号小方块。圆形障碍物K1、K2在直角坐标系下的圆心坐标分别为(350,400)、(200,-420)，半径分别为80mm、60mm。将可能发生碰撞的关节1取值区间划分为180个离散点，以充分逼近关节空间内的障碍区域。

采用MATLAB语言进行仿真试验，本避障规划算法进行路径规划的搜索时间为1.5449秒，仿真结果如图3至图5所示。

其中，图3为左右手系下的障碍区域；图4为关节坐标空间中二维避障路径的规划结果，左下角的绿色五角星为起始点，右上角的红色五角星为目标点，红色点阵为障碍区域，绿色点阵连线为避障路径，表示SCARA从大小臂均为负最大角度的位姿开始运动并依次规避两个圆形障碍物，到达大小臂均为正最大角度的位姿；图5为SCARA在直角坐标系下实现二维避障的动态演示过程，图中黑色为大臂每时刻状态，蓝色为小臂每时刻状态，绿色虚线为小臂末端的实际运动轨迹。

仿真结果表明，四轴机械臂SCARA能成功规避障碍物并完成预定的路径任务，实现从起始点到目标点的无碰撞运动。

图3 双手关节坐标系下的障碍物区域Fig.3 Obstacle region in the double-hand joint coordinate frame

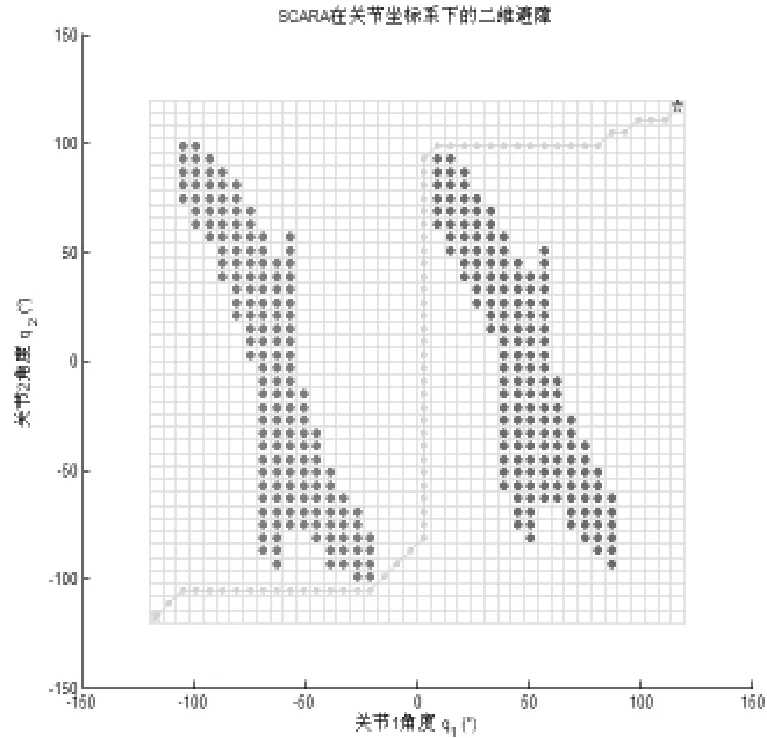
图4 四轴机械臂在关节坐标系下的二维避障路径Fig.4 Two-dimension obstacle-avoidance path of four-ax manipulator in joint coordinate frame

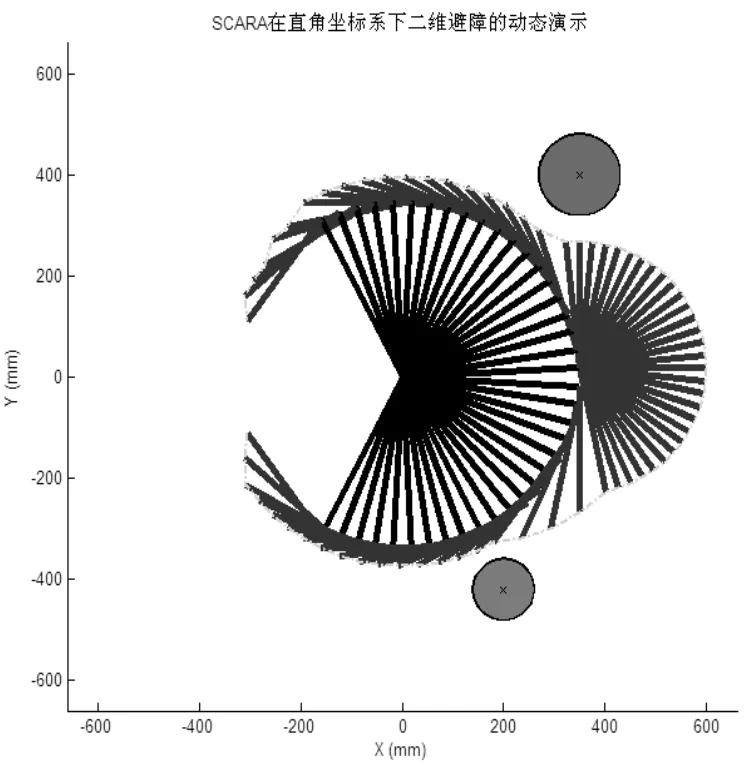
图5 四轴机械臂在直角坐标系下的二维避障动态过程Fig.5 Obstacle-avoidance dynamic process of four-ax manipulator in square coordinate frame

7 结 论

本文提出的智能平面搜索避障算法能有效规划出优化路径，成功解决四轴机械臂在平面内的障碍物避碰问题，具有一定的理论研究价值与较强的实际应用潜力。

需要特别指出的是，由于本算法基于图形中小方块的搜索，关节空间的细分精度对算法的效率影响较大。细分精度过高会降低搜索速度，过少则会降低搜索精度。因此，用户应根据工艺要求与实际情况适中取值，以使算法发挥其最大效用。

References)

[1]张捍东，董保华，岑豫皖，等. 栅格编码新方法在机器人路径规划中的应用[J]. 华中科技大学学报(自然科学版)，2007，35(1)：50-53.ZHANG Handong, DONG Baohua, CEN Yuwan, et al.Application of path encoding novel mechanism based on grids in path planning for mobile robot[J]. J. Huazhong Univ. of Sci. & Tech. (Nature Science Edition), 2007, 35(1):50-53. (in Chinese)

[2]M. Bennewitz, W. Burgard, S. Thrun. Finding and optimizing solvable priority schemes for decoupled path planning techniques for teams of mobile robots[J]. Robotics and Autonomous Systems, 2002, 41:89-99.

[3]王健强，程汀. SCARA机器人结构设计及轨迹规划算法[J]. 合肥工业大学学报(自然科学版)，2008，31(7)：1026-1028 +1041.WANG Jianqiang, CHENG Ting. Structural design and algorithms for trajectory planning of the SCARA robot[J]. J Hefei University of Technology (Nature Science Ed), 2008,31(7): 1026-1028+1041. (in Chinese)

[4]Suryawanshi A. B.，Jose M. B.，Dasgupta B.，et al.Domain mapping as an expeditionary strategy for fast pathPlanning[J]. Mechanism and Machine Theory，2003,(38)11-20．

[5]封岸松，戴炬. 冗余自由度机械手的避障控制[J]. 机器人，2002，24(3)：213-216.FENG Ansong, DAI Ju. Obstacle avoidance control abouredundant manipulator[J]. Robot, 2002, 24(3): 213-216.(in Chinese)

[6]田立中，付宜利，马玉龙， 等. 装配路径规划中基于动态坐标的A*搜索算法[J]. 计算机集成制造系统，2002，8(4)：316-319.TIAN Lizhong, FU Yili, MA Yulong, et al. A* Search arithmetic based on dynamic coordinate in assembly path plan[J]. Computer Integrated Manufacturing Systems, 2002,8(4): 316-319. (in Chinese)