基于温差均匀性原则的换热网络夹点设计法①
2013-12-10万义群崔国民彭富裕许海珠
万义群 崔国民 彭富裕 许海珠
(上海理工大学新能源科学与工程研究所)
换热网络是化工、冶金、石油、动力、环保等工业过程的重要工艺环节,对其进行综合优化在节约能耗和降低产品成本方面有着十分重要的意义。换热网络的综合及优化的方法主要可分为夹点设计法[1],数学规划法[2]和启发式方法[3-4]3大类。夹点设计法由英国学者Linnhoff和Hindmarsh于1983年首先提出,该方法基于热力学原理,以最大能量回收为目的设计换热网络,得到了工业上的广泛应用[5-6];数学规划法在换热网络 Grossmann超结构的基础上建立换热网络的混合整数非线性模型,对目标函数进行优化求解,但由于复杂换热网络具有严重的非线性和多峰性,使得此类方法难以获得全局最优解[7];启发式方法鲁棒性好,具有较好的全局搜索能力,但难以保证求解的质量和效率。
夹点设计法是目前实际应用中最为成功的一种方法,夹点设计的方法主要分为3个步骤:
(1)给定最小允许传热温差,确定夹点位置;
(2)在夹点处将换热网络分成两个独立的子系统,每个子系统按照一定的规则合理匹配物流设计网络结构;
(3)对网络初始结构进行调优,获得最优的网络结构。夹点设计法的关键在于物流的匹配设计,夹点将换热网络分成冷端和热端两个子系统单独处理,从夹点开始向两端匹配,夹点处的匹配条件最为苛刻,远离夹点处的匹配较为宽松,虽然有许多夹点匹配可行性准则及经验规则[8]指导物流匹配,但由于换热网络极为复杂,使得匹配的效果在很大程度上依赖于设计者的经验。
过增元院士从换热器沿程温差与换热效能的关系出发,提出了两股流换热器的温差均匀性优化原则[9-10],依据该原则对换热器进行改进能够提高换热器的换热效能;文献[11]将温差均匀性优化原则应用在多股流换热器上,建立了多股流换热器设计的温差均匀性因子,能够用于衡量多股流换热器通道排列的优劣,从而指导多股流换热器的优化设计;文献[12-14]从换热网络整体强化的角度出发提出了换热网络的温差均匀性优化原则,建立了换热网络的温差均匀性因子,以期为换热网络的换热效能提供一种新的评价指标,并能指导换热网络的优化设计。
鉴于此,本文将温差均匀性因子作为定量的评价指标来指导换热网络结构的设计,提出了一种基于温差均匀性原则的换热网络夹点设计法对传统的夹点设计法进行改进,在此原则下获得的换热网络初始结构具有较好的换热性能,然后采用牛顿法优化初始结构使换热单元数及换热单元面积得到优化,从而达到使换热网络的年综合费用最低的目的。
1 换热网络数学模型
1.1 数学模型
本文的换热网络模型采用无分流分级超构模型,以NH表示热流体的数目,NC表示冷流体的数目。以2股热流体和3股冷流体为例,其无分流的换热网络超结构如图1所示,H1、H2表示热流体,C1、C2、C3表示冷流体。将所有冷、热流体的换热组合记为一个级,每种换热组合可匹配一个换热器,1级换热网络内的换热器数目最大为6个。换热网络的级数为NK,NK=max(NH,NC),换热网络最大换热器个数可以达到NH×NC×NK。冷、热公用工程分别加在最后一级的后面和第一级的前面。

1.2 目标函数
以换热网络的年综合费用F为目标函数,其包括投资费用及公用工程费用,投资费用包括固定投资费用和面积费用,公用工程费用可分为热工用工程费用和冷公用工程费用,目标函数的表达式如下:

式中:QCU,i、QHU,j分别 为 冷、热 公 用 工 程 换 热量,kW;CCU、CHU分别为冷、热公用工程费用系数,$/(kW·a);ACU,i、AHU,j、Ai,j,k分别为冷公用工程单元、热公用工程单元和换热器单元的换热面积,m2;C1、C2、C3分别为冷公用工程单元、热公用工程单元和换热器单元的固定投资费用,$/(台·a);C′1、C′2、C′3分别为冷公用工程单元、热公用工程单元和换热器单元的面积费用系数,$/(m2·a);B为面积费用指数。
1.2.1 约束条件
出口温度约束:

式中:tH,i,out、tC,j,out分别为 热 流 体和冷流体 的 出口温度,℃;tH,i、tC,j分别为热流体和冷流体的目标温度,℃。
1.2.2 换热单元面积约束
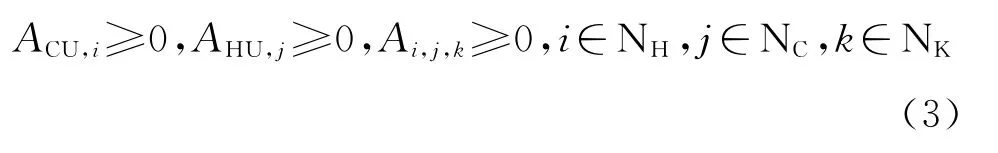
式中:ACU,i、AHU,j和Ai,j,k分别为冷公用工程单元、热公用工程单元和换热器单元的面积,m2。
1.2.3 换热单元换热量约束

式中:QCU,i、QHU,j和Qi,j,k分别为冷公用工程单元、热公用工程单元和换热器单元的换热量,kW。
2 基于温差均匀性原则的换热网络夹点设计法
文献[13]从换热网络的换热效能出发,提出了换热网络的温差均匀性原则,该原则指出换热网络的温差场越均匀则整个换热网络的换热性能越好,并通过对换热网络温差场的分析,建立了基于换热网络离散温差场的温差均匀性因子,其建立的温差均匀性因子表达式如下:

式中:n为换热器的台数,台;Δti为第i个换热器的对数平均温差,℃。
通过具体的实例对换热网络离散温差均匀性因子进行验证,可以得出温差均匀性因子越小则换热性能越好的结论。本文将换热网络的组合曲线进行分段处理,则在一段范围内换热网络的温差均匀性因子能较准确地反映该段的换热性能。将换热网络的温差均匀性因子作为评价指标指导网络结构的设计,从场协同理论[15-16]的角度来说,这样设计的网络结构具有良好的换热性能。
Linnhoff和Hindmarsh所提出的夹点设计法的基本原则[17]有:
(1)在夹点处分解问题,对每一部分进行单独设计;
(2)从夹点处开始设计,向外拓展;
(3)接近夹点处有两个限制:在夹点之上,对所有热物流CPHOT≤CPCOLD;在夹点之下,对所有冷物流CPHOT≤CPCOLD;
(4)使热负荷最大化;
(5)只在夹点以上提供热公用工程,只在夹点以下提供冷公用工程。
其他网络设计原则有夹点匹配可行性准则及经验规则等,按照这些原则设计的网络结构众多,目前没有定量的衡量指标来评价结构设计的优劣,本文引入温差均匀性因子作为评价指标来指导换热网络的初步设计。
初步设计的换热网络需要通过调优以简化结构,从而达到降低综合费用的目的。调优的本质是调节投资费用与公用工程费用之间的竞争关系,一般的方法[18]是断开热负荷回路,实现热负荷回路的能量松弛,在提高能量回收率的基础上减少换热单元数。由于换热网络初始结构较复杂,该方法工作量大,目前已有许多学者应用数学规划法及开发相应的软件[19-20]来对初始结构进行调优,这些方法对于权衡换热网络投资费用与公用工程费用之间的关系具有较高的效率和较好的效果。本文将建立换热网络的数学模型,以年综合费用为目标函数,换热单元面积为变量,采用经典的牛顿法对初始结构进行优化,以此达到调优的效果。
本文提出的换热网络综合优化方法具体步骤如下:
(1)给定最小传热温差,确定夹点位置;
(2)从夹点位置开始,按照热流体或冷流体的进出口温度分成较光滑的若干段;
(3)将每段中包含的冷热物流进行换热匹配,使得能量得到最大化利用。由于分段后换热流股数及换热器单元个数都将减少,可以采用穷举的方法匹配出所有可行的结构,规定用两端的温度约束进出口温度,每次匹配都耗尽一股流体的换热量;
(4)计算每段匹配结构的温差均匀性因子,取因子最小值对应的结构,将各段获得的结构及远离夹点处的匹配组成完整的换热网络结构;
(5)采用牛顿法优化各换热器单元的面积,以此获得年综合费用最优的换热网络结构。
3 算例分析
本算例取自文献[21],该算例由6股热流体和4股冷流体组成,各流体的参数在表1中给出。换热器费用计算公式为:60×A(m2)$;各股流体的传热系数均为0.05kW/(m2· ℃);热公用工程费用系数为100$/(kW·a),冷公用工程费用系数为15$/(kW·a)。

表1 10股流换热网络的物流参数Table 1 Parameters of streams for 10 streams heat exchanger networks
取Δtmin=16.0℃,A为夹点位置,对应的热流体温度为56.0℃,对应的冷流体温度为40.0℃,从夹点位置处开始将组合曲线图进行分段处理,B处对应的热流体温度为85.0℃,对应的冷流体温度为53.1℃,C处对应的热流体温度为99.97℃,对应的冷流体温度为65.0℃,组合曲线及其分段如图2所示。
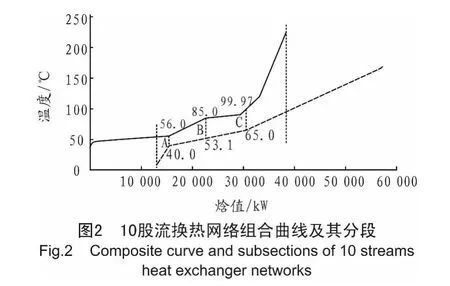
对分段的各部分进行单独设计,AB段包含的换热流体有 H1、H2、H3、H6、C1和C4,这些流体进行匹配换热,计算每种匹配结构的温差均匀性因子,AB段的匹配结构如图3所示(列举部分结构,图中数字为换热器进出口温度,℃),参数见表2。从表2中可以看出,结构一与结构二的匹配使得该部分的出口温度与总换热量相同,但结构一对应的温差均匀性因子最小,说明这种匹配使得该段的温差更均匀,换热性能更好。


表2 AB段设计结构的参数Table 2 Parameters of design structures of AB segment
BC段包含的换热流体有 H2、H3、H5、H6、C1、C2和C4,BC段的匹配结构如图4所示(列举部分结构,图中数字为流体进出口温度,℃),参数见表3。从表3中可以看出,结构三对应的温差均匀性因子最小,说明这种匹配使得该段的温差更均匀,换热性能更好。


表3 BC段设计结构的参数Table 3 Parameters of design structures of BC segment
将AB段和BC段设计的结构以及远离夹点处的匹配组合成一个完整的换热网络结构,然后采用牛顿法优化各换热器单元的面积,最终获得的结构如图5所示(图中数字为流体进出口温度,℃),与其它文献的结果比较见表4。从表4中可以看出,本文优化的结构所耗公用工程量少,具有良好的换热性能,且通过牛顿法的优化使得年综合费用优于其它方法得到的结果。


表4 优化结果对比Table 4 Comparisons of optimization results
4 结论
在温差均匀性原则的基础上,改进传统的夹点设计法对换热网络进行优化。针对传统方法中物流匹配的难点,引入温差均匀性因子作为定量的评价指标指导物流匹配设计网络结构,这种方法设计的网络结构能够保证换热网络整体的温差均匀性和良好的换热性能。采用牛顿法优化初始网络结构中换热器的面积来权衡投资费用及公用工程费用,以此取代传统方法中调优的复杂工作。通过具体的算例分析可知,该方法设计的换热网络结构具有较好的换热性能,且获得了优于其他文献的结果,证明了该方法的可行性和有效性。
[1]Linnhoff B,Hindmarsh E.The pinch design method for heat ex-changer networks[J].Chemical Engineering Science,1983,38(5):745-763.
[2]Yee T F,Grossmann I E.Simultaneous optimization for heat integration-II.Heat exchanger network synthesis[J].Comput.Chem.Eng.,1990,14(10):1165-1184.
[3]Ravagnani M A S S,Silva A P,Arroyo P A,et al.Heat exchanger network synthesis and optimization using genetic algorithm[J].Appl.Therm.Eng.,2005,25(7):1003-1017.
[4]Lin B,Miller D C.Solving heat exchanger network synthesis problems with Tabu search[J].Comput.Chem.Eng.,2004,28(8):1451-1464.
[5]朱玉琴,秦倩倩,卞雯,等.气体分馏装置的节能优化[J].石油与天然气化工,2012,41(2):243-252.
[6]王毅,王震权,范金禄.换热系统夹点温度计算[J].石油与天然气化工,2010,39(S1):44-46,49.
[7]胡向柏,崔国民,涂惟民.复杂换热网络MINLP中的非线性特征分析[J].工程热物理学报,2012,33(2):285-287.
[8]葛玉林.常减压蒸馏流程模拟与优化及换热网络综合[D].大连:大连理工大学,2007.
[9]过增元,李志信,周森泉,等.换热器中的温差场均匀性原则[J].中国科学,1996,26(1):25-31.
[10]过增元.热流体学[M].北京:清华大学出版社,1992.
[11]吕岩岩,崔国民,郭佳,等.多股流换热器设计的量纲Ⅰ温差均匀性优化因子[J].化工学报,2007,58(10):2476-2480.
[12]崔国民,吕岩岩,张勤.换热器网络温差场分析及温差均匀性因子的建立[C]//中国工程热物理学会传热传质学术会议论文集,2006:1608-1611.
[13]吕岩岩.场协同下的换热器网络整体强化技术研究[D].上海:上海理工大学,2009.
[14]崔国民,吕岩岩,胡向柏.换热网络整体强化技术及其温差均匀性因子[C]//中国工程热物理学会传热传质学术会议论文集,2008:454.
[15][德]哈肯 H.协同学:理论与应用[M].杨炳弈,译.第一版.中国科学技术出版社,1990.
[16]过增元,黄素逸.场协同原理与传热强化新技术[M].北京:中国电力出版社,2004.
[17][英]伊恩C肯普.项曙光,著.贾小平,夏力,译.能量的有效利用:夹点分析与过程集成[M].北京:化学工业出版社,2010.
[18]Su J L,Motard R L.Evolutionary synthesis of heat-exchanger networks[J].Comput.Chem.Eng.,1984,8(2):67-80.
[19]李有润,R I Motard.计算机辅助换热网络两步法优化综合[J],化工学报,1990,41(2):254-254.
[20]张平,何小荣.换热网络改造综合中初始网络调优的专家系统[J],计算机与应用化学,2002,19(3):218-222.
[21]Ahmad S.Heat exchanger networks:Cost trade-offs in energy and capital[D].UMIST,Manchester,UK,1985.
[22]Yerramsetty K M,Murty C V S.Synthesis of cost-optimal heat exchanger networks using differential evolution[J].Comput.Chem.Eng.,2008,32(8):1861-1876.
[23]Khorasany R M,Fesanghary M.A novel approach for synthesis of cost-optimal heat exchanger networks [J].Comput.Chem.Eng.,2009,33(8):1363-1370.
