贯流机组主轴疲劳强度计算及其影响因素分析

2013-12-10李永恒

上海大中型电机 2013年1期

李永恒

(哈尔滨大电机研究所，黑龙江哈尔滨 150040)

0 引言

水轮发电机组主轴是实现水轮机与发电机之间扭矩传递的关键部件。如果出现问题，轻则影响电站的运行，重者造成安全事故。

主轴的支撑是通过组合轴承和水导轴承。组合轴承限制主轴的径向位移和轴向位移，水导轴承限制主轴的径向位移。发电机转子和水轮机转轮以悬臂梁式安装在主轴上，主轴两端靠法兰与转轮和发电机转子相连接。工作过程中，主轴要承受轴向水推力、转轮浮力、转轮体装配重力以及主轴传递的扭矩。贯流式水轮机采用卧轴布置结构，由转轮浮力和转轮体装配重力会引起的弯矩，产生交变应力，且主轴有些部位处于水介质中，更容易出现疲劳破坏。

1 疲劳强度及载荷

承受变载荷的结构，其结构的疲劳破坏是在不同频率和幅值的载荷作用下所造成的损伤逐渐累积的结果。一个结构的破坏过程是从裂纹萌生，到扩展，最后是零件材料断裂失效。自1870年提出SN曲线和疲劳极限的概念以来，众多学者对疲劳损伤的研究进行了大量的探索。

影响疲劳损伤的因素有很多，其中主要因素有:载荷、材料、环境条件、结构的形状与几何尺寸。用相同材料制造的相同几何尺寸的结构在相同服役环境下，疲劳损伤量主要与载荷。载荷对疲劳损伤量的影响主要体现在载荷的变化过程，即应力循环特性R或应力幅和应力均值σm。

1.1 非对称循环应力

如果结构是在循环等幅对称载荷作用下工作的，则结构的S-N曲线方程为:

式中:

σ——对称应力循环的应力幅;

M——与应力σ相对应的失效循环次数;

σ-1——对称应力循环的疲劳极限;

N0——与疲劳极限σ-1相对应的失效循环次数;

m——材料常数，即对称应力循环下S-N曲线的对数斜率。

但笔者分析的主轴是在非对称载荷下工作的，对于这种情况，根据材料的不同特性，工程上常常采用简化的极限应力曲线进行等效。对于脆性材料(如主轴材料ZG20SiMn)，采用简化的Goodman方程进行等效。

非对称应力循环的转换满足关系式:

式中:

σ-1cr——非对称应力循环等效为对称应力循环的等效应力;

σRa——非对称应力循环的应力幅值;

σRm——非对称应力循环的应力均值;

Ψσ——将应力均值转化为应力幅值的等效系数。

1.2 等效循环对称应力

S-N曲线是由标准光滑试件在对称循环交变应力下测得的。但主轴的疲劳极限还受很多疲劳因素的影响，例如尺寸大小、缺口应力集中、表面质量、平均应力等。因此，必须对由标准光滑小试件在对称循环交变应力下测得的疲劳强度进行适当修正，才能对主轴进行疲劳强度计算。考虑这些因素影响后，可以得到主轴工作应力等效为循环对称应力的计算公式如式(3)。

式中:

Kσ——有效应力集中系数;εσ——结构尺寸系数;

β——表面加工系数;

Ψσ——平均应力影响系数。

由式(3)可以得到主轴的疲劳安全系数:

式(4)中:

c——为载荷影响系数(水力不平衡力、转轮不平衡力);

σ-1——对称循环下的疲劳极限。

2 某贯流机组主轴疲劳强度分析

从疲劳安全系数的计算公式中可以看出，有效应力集中系数、结构尺寸系数、平均应力影响系数对主轴疲劳强度有很大的影响。但这些系数的选取都是根据经验公式，且使用这些公式时受到适用条件、参数取值范围及应用场合的影响。但是随着有限元的发展，用有限元软件可以较全面地分析主轴的应力和变形，并且结果会更准确。笔者应用有限元法对某电站主轴的疲劳强度进行计算，并对其影响因素进行分析。

2.1 某贯流机组的基本参数

最大功率:Nmax=49 WM

额定转速nr=107.1 r/min

轴向水推力:F1=685 T，转轮体配重G=71 T

转轮浮力:F2=13 T，法兰厚度a=220 mm

法兰面到转轮重心距离:L1=1 163.5 mm，法兰面到转轮浮力中心距离:L2=1 600 mm

材料:ZG20SiMn

假设机组利用系数为0.85，每年365天，则一年的旋转次数为:

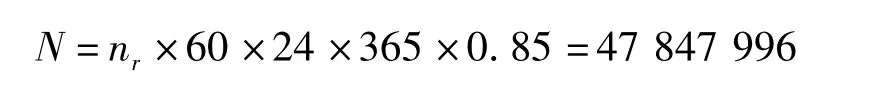
2.2 有限元计算模型

为了使结果更准确，取整个主轴作为计算模型。约束主轴台阶和静板接触面的轴向位移，限制水导轴承、发导轴承支撑面的径向位移。由于转轮的结构比较复杂，笔者分析时没有建转轮模型，而是在法兰端面建立一个刚性面，通过在刚性面上施加弯矩来代替由转轮重力和浮力引起的弯矩。考虑的载荷包括轴向水推力、转轮浮力、转轮体装配重力以及主轴传递的扭矩。重点分析的位置是转轮端法兰圆角(a-a剖面)及主轴上的凹槽(b-b剖面)，如图1所示。这两个部位的工作介质都是水。为了更准确的反应这个部位的应力，对这两个部位的网格划分的很密，有限元模型如图2所示。

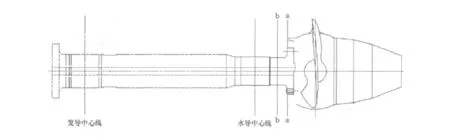
图1 卧式主轴危险截面位置示意图

图2 主轴有限元分析模型

2.3 应力集中系数

疲劳裂纹一般产生在应力集中较严重的地方，首先分别计算了法兰圆角和主轴凹槽两个位置的弯曲、扭转、拉伸应力集中系数。并通过改变法兰圆角和主轴凹槽的大小来验证几何尺寸对应力集中系数的影响。计算时采用的载荷扭矩Mt=1E6 N·m，弯矩 Mb=1E6 N·m，P=-1 MPa。

应力集中系数表示最大实际应力与根据所加载荷和具体结构尺寸计算的名义应力之比。

主轴扭转应力集中系数ατ等于表面最大切应力τmax与轴名义切应力之比τn，即:

ατ=，其中名义切应力τn=，式中 Mt为计算扭矩，模拟主轴所受的扭矩，Wτ主轴名义抗扭截面模量。

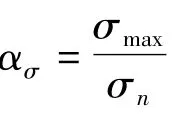
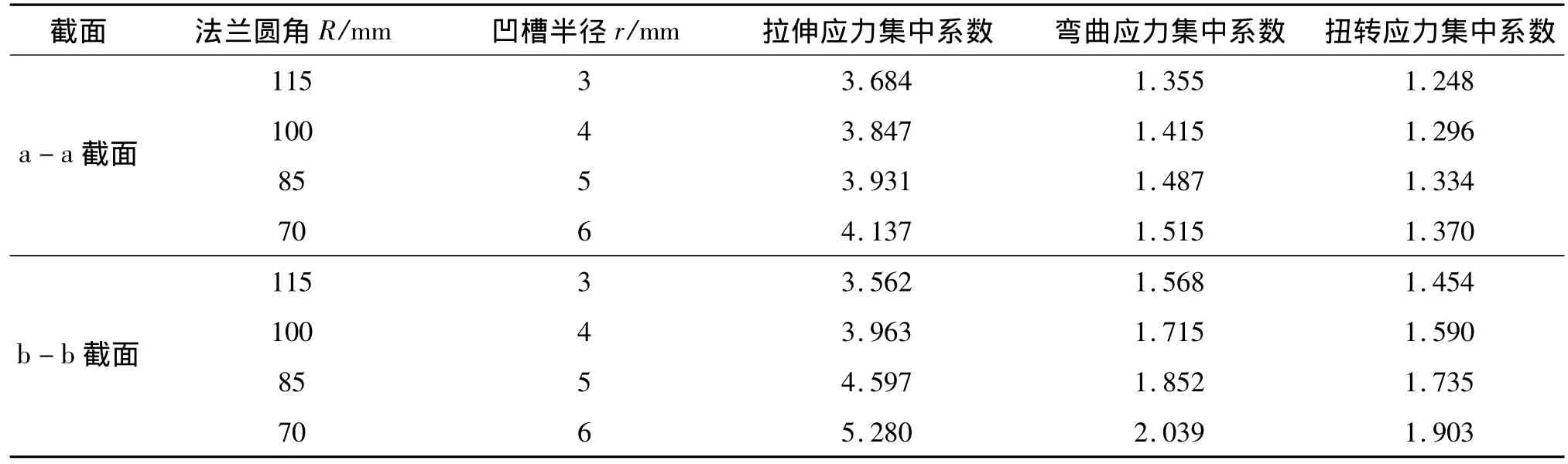
表1 不同尺寸时两个截面的应力集中系数

法兰圆角R=115 mm，凹槽半径r=3 mm时，弯曲正应力、扭转切应力、拉应力一次如图3～5所示。

图3 弯曲状态下的拉应力示意图

图4 扭转状态下的切应力示意图

图5 拉应力下的拉应力示意图

2.4 疲劳寿命

在主轴的实际工作载荷下，分别计算了不同法兰圆角、凹槽大小时，两个危险截面的疲劳寿命。

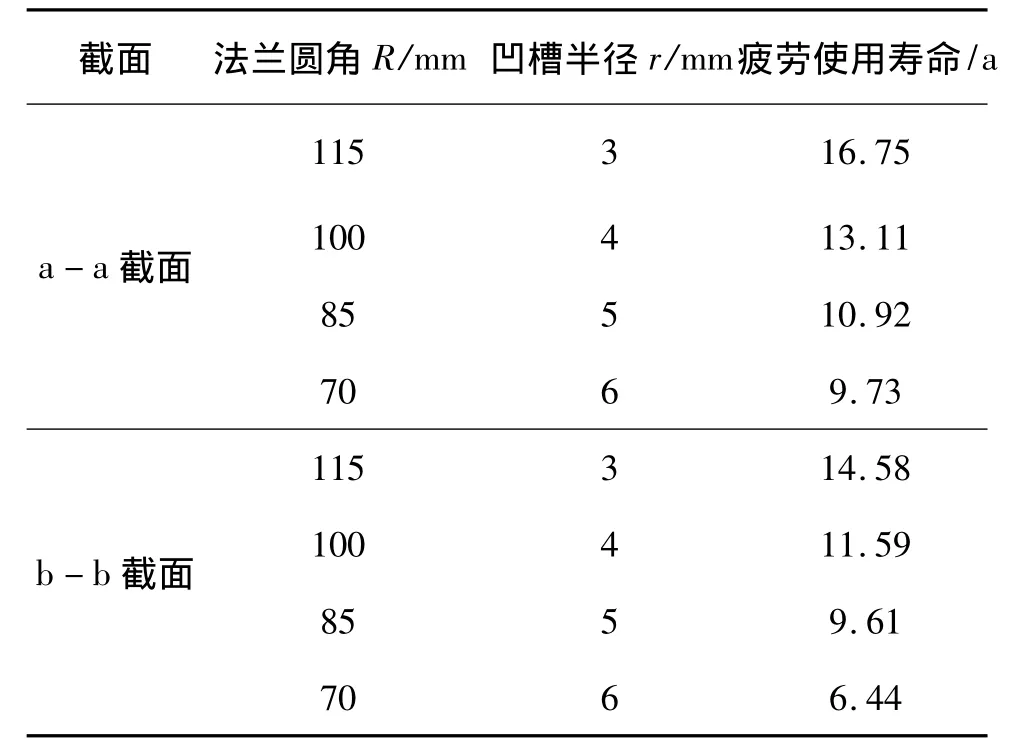
表2 不同尺寸时两个截面的疲劳寿命

从表2可以看出，对于截面b-b，随着凹槽的增大，主轴的使用寿命明显降低，对于截面a-a，随着法兰圆角的减小主轴使用寿命随之减小，但变化不像凹槽处那么明显。通过表1与表2的对比可以看出，两个截面寿命的变化趋势与截面处的应力集中系数的变化趋势相同。从表2可以看出，主轴上的凹槽对疲劳寿命影响太大，所以能不出现凹槽最好不要出现。

法兰圆角R=115 mm，凹槽半径r=3 mm时，主轴的等效应力分布云图如图6所示。