支撑钢框架中关键柱破坏后结构抗倒塌性能分析
2013-12-08高山,魏民,徐嫚
高 山,魏 民,徐 嫚
(1.哈尔滨工业大学 土木工程学院,黑龙江 哈尔滨 150090;2.列日大学 应用科学学院,列日 4000;3.大庆油田设计院,黑龙江 大庆 163712;4.东北林业大学 土木工程学院,黑龙江 哈尔滨 150040)
0 引 言
自从1968年英国Ronan Point公寓发生连续倒塌事件以来,结构的抗倒塌性能研究和设计一直备受全球学者和工程设计人员的关注,而在1996年美国Alfred P.Murrah联邦大楼和2001年世贸中心接连发生的结构连续倒塌事件,更是引发了世界范围内对结构抗连续倒塌的研究热潮。根据ASCE的定义,结构连续倒塌是指结构受到意外荷载的作用而产生局部破坏向其他单元扩展,最终导致结构整体或与初始破坏不成比例的倒塌[1]。
很多国家都制定了相应的规范以防止结构在关键构件破坏后发生连续性倒塌,如英国规范BS 8110-1:1997[2]、欧洲规范 EN 1991-1-7:2003[3]、美国公共事务管理局规范GSA 2003[4]、美国国防部规范 UFC 4-023-03[5]等。综合各国的抗倒塌设计规范,可将结构抗连续倒塌设计方法分为直接设计法和间接设计法,前者主要是定量设计,如拉结力法和局部加强法;后者主要是定性设计,如采用规则的结构体型和合理的构件布置等。中国对于结构抗连续倒塌的研究相对较少,一些学者针对结构抗连续倒塌分别做了一些试验和理论的研究[6-10],但中国规范中仅给出了少许定性设计条款,并未给出详细的设计方法。
在结构体系的抗连续倒塌分析中,主要采用的是线弹性静力分析、非线性静力分析及非线性动力分析。当结构中的关键柱突然发生破坏时,相当于在很短时间内将其所受荷载转移到与失效柱相连的构件和节点上,并带来一定的动力冲击作用,因此,结构连续倒塌实质上是一个非线性动力过程,故在所有方法中以非线性动力分析最接近实际结构发生连续倒塌时的反应。由于非线性动力分析涉及到复杂的动力特性和材料非线性、几何非线性的非线性问题,所以常用于分析大跨度、超高层和复杂建筑结构。
中心支撑作为一种性能优良、构造简单的耗能元件,常用于抗震设计中以抵抗水平荷载;而偏心支撑则作为近年来新型的支撑形式被广泛用于大震作用下结构的抗震设计中,其具有耗能性能优越、造价低等优点。鉴于抗震设计和抗倒塌设计在一定程度上具有共通性,中心支撑和偏心支撑也可以作为抗倒塌构件用于结构的抗倒塌设计中,以抵抗竖向荷载,实现内力的重新分配[11-12]。本文中笔者将采用瞬时拆柱法,对竖向分布荷载作用下,采用不同支撑形式的平面支撑钢框架进行非线性动力反应分析,以研究结构连续倒塌时的动力效应。
1 分析方法
采用瞬时拆柱法对结构进行连续倒塌动力反应分析,如图1所示,其中,q为作用在剩余结构上的竖向均布荷载。首先在结构上施加均布荷载,即结构的使用荷载;然后在保持上一步荷载的基础上,在一定时间内拆除结构的某关键柱,以模拟结构构件的失效,从而对结构进行弹塑性动力分析,如图2所示,其中,P为失效柱的内力,P0为柱底在使用荷载下的反力,t为时间,tf为构件的失效时间,即柱的内力在tf时降为0。根据文献[4]中的规定,失效时间取为剩余结构基本周期T的10%。本文中采用有限元软件ABAQUS进行建模,并进行非线性动力分析。

图1 瞬时拆柱法分析步骤Fig.1 Analytical Steps of Instantaneously Removal Column Method
对于移除失效构件后的剩余结构,采用需求能力比IDCR作为分析参数,需求能力比IDCR的定义为:竖向均布荷载与剩余结构的极限竖向均布荷载之比,即

式中:qu为剩余结构的极限竖向均布荷载,由Pushdown(竖向静力推覆)曲线获得。
2 分析对象及参数

图2 P-t曲线Fig.2 P-t Curve
本文中根据某民用多层住宅设计了1榀6跨12层平面钢框架并对其进行分析,跨度均为6m,层高均为3.6m,并在此框架的基础上,同时在左右两边跨及两中间跨处布置3种中心支撑和2种偏心支撑,包括X型中心支撑、V型中心支撑、反V型中心支撑、V型偏心支撑和反V型偏心支撑。图3为布置支撑的框架。所有梁、柱及支撑均采用轧制H型钢,梁型号为HN450×200×10×14,第1~4层柱型号为HW400×400×13×21,第5~8层柱型号为HW350×350×12×19,第9~12层柱型号为HW300×300×10×15,支撑采用HW175×175×7.5×11。根据文献[11]中的研究,在无特殊要求下,偏心支撑耗能梁段的长度可取梁长的10%~15%,本文中取15%的梁长,即900 mm。梁、柱及支撑均采用HRB335钢材,钢材弹性模量取206GPa,密度取7.85×103kg·m-3,钢材材料本构选用四段式二次塑流本构。选用ABAQUS单元库中的梁单元B31来模拟框架中的梁、柱及支撑,所有梁上均作用大小相同的竖向均布荷载,分别考虑底层边柱C1和中柱C4失效时剩余结构的动力反应。
为了验证模型的正确性,选取文献[12]中所进行的两层单跨(试件PF3)和两层两跨(试件PF4)钢框架水平推覆试验进行验证。图4为有限元模型和试验试件的水平荷载-位移曲线对比。由图4可以看出,模拟结果和试验结果拟合良好,因此采用四段式二次塑流钢材本构和B31梁单元可以很好地模拟钢框架的力学性能。

图3 框架立面(单位:mm)Fig.3 Elevation Drawings of Frames(Unit:mm)
对边柱C1和中柱C4失效后的剩余结构分别进行模态分析,可以得到模型的基本周期T及前2阶自振角频率ω1,ω2。通过采用瑞利阻尼的形式考虑阻尼对结构的影响,可根据剩余结构的前2阶自振角频率及阻尼比求得结构的阻尼。根据《钢结构设计规范》(GB 50017—2003),结构的阻尼比取为0.02。对边柱C1和中柱C4失效后的剩余结构进行Pushdown分析,各框架的分析参数如表1所示,其中,α,β分别为质量阻尼系数和刚度阻尼系数。从表1可以看出,支撑框架的自振角频率均超过无支撑框架的2倍,支撑的布置大大提高了结构的刚度。

图4 水平荷载-位移曲线对比Fig.4 Comparisons of Lateral Load-displacement Curves
3 分析结果
3.1 Pushdown曲线
图5为边柱C1和中柱C4破坏后框架的Pushdown曲线,纵坐标为梁上均布荷载,横坐标为失效柱上部的节点竖向位移。由图5可以看出:各支撑框架边柱C1失效的结构的Pushdown曲线均在中柱C4失效的结构的曲线下方,边柱失效对于结构来说更为不利。支撑框架的刚度要远大于无支撑框架,但极限承载力的提高并不像刚度那样明显。同时,支撑框架的Pushdown曲线较无支撑框架有明显的线性。当结构失效时,失效柱处的节点位移较小,结构表现为突然破坏,这主要是因为支撑设计为两端固接;当柱失效时,支撑多为压弯杆,在较大的荷载作用下很容易出现失稳。由于框架梁、柱节点为刚接,所以无论是否设置支撑,在失效节点处均无法有效形成“悬索作用”,梁中轴力均较小。
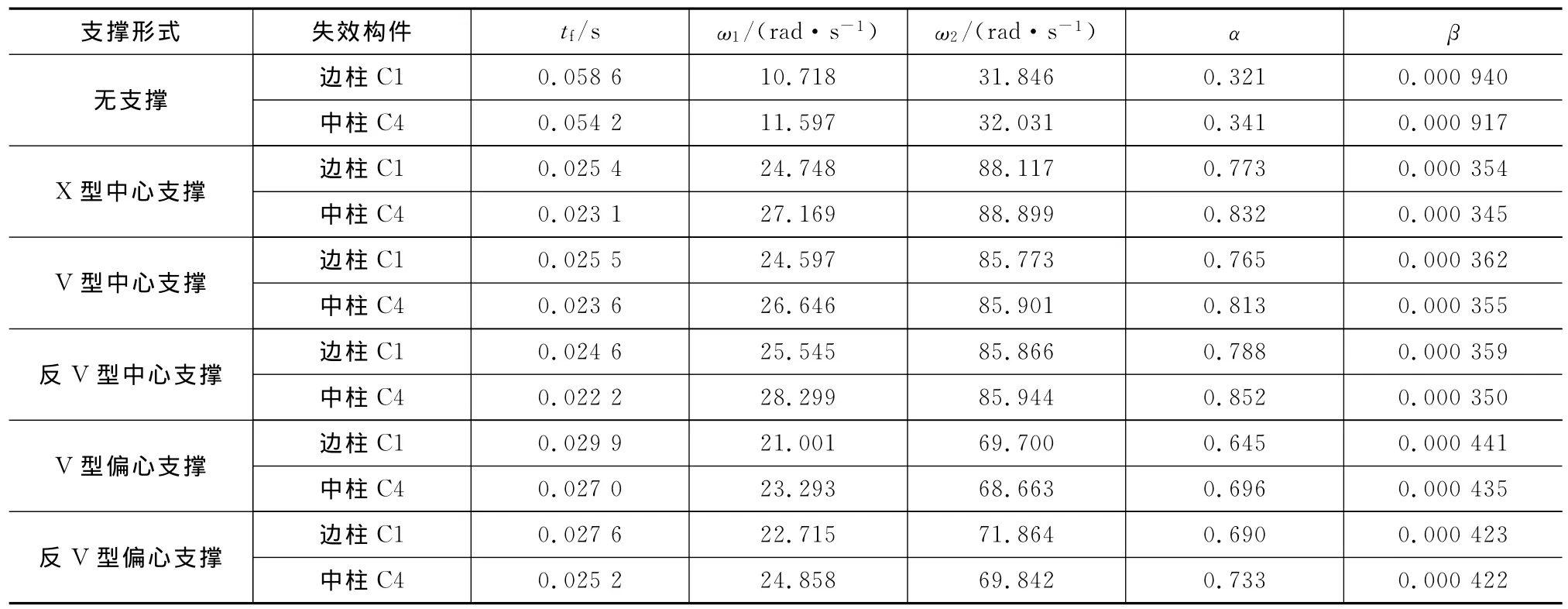
表1 各框架的分析参数Tab.1 Analytical Parameters of Each Frame
由图5还可以看出,V型中心支撑和V型偏心支撑的均布荷载-位移曲线的屈服点并不明显,而X型中心支撑、反V型中心支撑和反V型偏心支撑的均布荷载-位移曲线则具有明显的拐点,在到达屈服点后曲线刚度明显降低,这是由于X型中心支撑和反V型支撑在均布荷载作用下将承受压力作用,因此当受压的支撑失稳时框架的刚度将明显降低,而V型支撑则承受拉力的作用,不会出现明显影响框架刚度的失稳现象。
表2为Powndown曲线中柱失效后各支撑框架的刚度对比,其中,Ei,Es分别为无支撑框架中柱失效和边柱失效后剩余结构的刚度(Ei=1.3Es);支撑框架的刚度以无支撑框架刚度的倍数来表示。从表2可以看出,当中柱失效时,X型中心支撑对于刚度的提高最为明显,V型中心支撑的提高幅度要略高于反V型中心支撑,2种偏心支撑的提高幅度要小于相应的中心支撑。对于边柱失效的情况,X型中心支撑同样提高幅度最大,而2种偏心支撑的提高幅度最小。值得注意的是,V型中心支撑和V型偏心支撑框架在边柱失效和中柱失效时的刚度变化不如无支撑框架和其他支撑形式框架明显,可见,在提高结构刚度方面,无论是设置为中心支撑还是偏心支撑,V型支撑的效果不如X型中心支撑和反V型支撑。
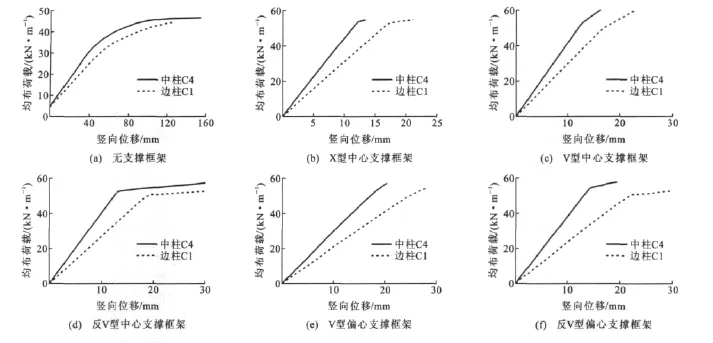
图5 均布荷载-竖向位移曲线Fig.5 Uniformly Distributed Load-vertical Displacement Curves

表2 柱失效后框架刚度Tab.2 Stiffness of Frames After Column Failed
表3为中柱失效和边柱失效后框架能承担的极限均布荷载。与刚度类似,中柱失效后结构的极限均布荷载均要大于边柱失效后的结构。以IDCR为参数,由式(1)可以得到不同IDCR所对应的均布荷载,然后采用瞬时拆柱法对剩余结构进行结构连续倒塌动力反应分析。

表3 柱失效后框架极限均布荷载Tab.3 Ultimate Uniform Loads of Frames After Column Failed kN·m-1
3.2 位移时程曲线
图6为各支撑框架在中柱失效和边柱失效时对应节点的竖向位移时程曲线。从图6可以看出:对于中柱失效的结构,竖向位移均是单调增加至最大值,继而上下波动衰减,逐渐趋于稳定;对于边柱失效的结构,无论是否设置支撑,竖向位移总是在第3个波峰才达到峰值位移,而设置支撑会大大缩短峰值位移到达的时间,剩余结构在较短时间内快速振动并达到峰值位移。当失效时间达到1s时,对于中柱失效的框架其失效点位移基本趋于稳定,而对于边柱失效的框架,其失效点位移仍有一定幅度的振荡,设置支撑并没有起到缓解振荡的作用。
对于无支撑框架,当中柱失效时,随着IDCR的增大,峰值位移由7.8mm增大至94.4mm,所对应的时间由0.068s增大至0.094s;当边柱失效时,随着IDCR的增大,峰值位移由10.5mm增大至134.2 mm,所对应的时间由0.287s增大至0.323s。由此可见,边柱失效时结构的峰值位移更大,出现的时间更晚。
对于有支撑框架,无论中柱失效还是边柱失效,不同IDCR下的峰值位移均明显减小,峰值位移出现的时间也有不同程度的提前。对于同一榀有支撑框架,结构峰值位移的出现时间并没有像无支撑框架那样,随着IDCR的增加有明显的增大。
当中柱失效时,各支撑框架的峰值位移出现的时间相差不多。在不同IDCR下,X型中心支撑框架的峰值位移均最小,其次为V型中心支撑和反V型中心支撑框架,V型偏心支撑和反V型偏心支撑框架最大;当边柱失效时,X型中心支撑和V型中心支撑框架的峰值位移接近,两者的峰值位移最小,其次为反V型中心支撑框架,而V型偏心支撑和反V型偏心支撑框架的峰值位移要明显大于其他形式支撑框架。
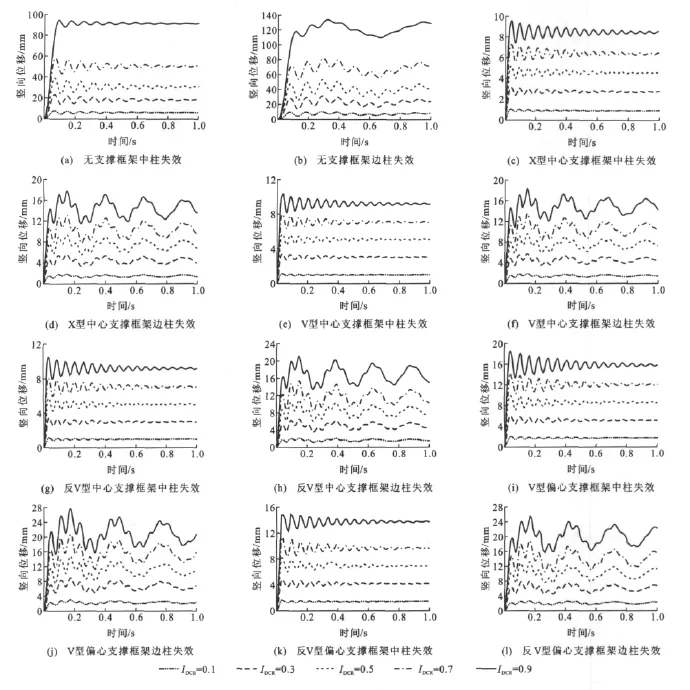
图6 竖向位移时程曲线Fig.6 Vertical Displacement Time History Curves
3.3 轴力时程曲线
图7为无支撑框架底层柱失效后其临柱的轴力时程曲线。由图7可以看出,轴力时程曲线的趋势与失效点的位移时程曲线类似。当底层柱失效时,临柱的内力增大,均在原内力的1.5倍以上,当边柱失效时,临柱的内力放大效应要大于中柱失效的结构。随着IDCR的增大,临柱内力增大的趋势略有降低,对于中柱失效的结构,临柱内力的放大系数从1.71减小至1.58,对于边柱失效的结构,临柱内力的放大系数从1.96减小至1.79。
表4,5中分别给出了中柱失效和边柱失效后临柱的内力最大值随IDCR的变化情况。从表4,5可以看出,虽然支撑可以有效地抑制失效点的位移,但除了V型中心支撑和V型偏心支撑外,在不同IDCR下,其他形式的支撑对临柱的内力都影响不大(由于各级IDCR下结构上的均布荷载不同,各级内力均较原结构内力略大)。而对于V型支撑,由于其构造形式特点,一部分荷载通过支撑直接传向了基础,因此其临柱的内力较原结构和其他支撑结构小;V型中心支撑在传力路径上比V型偏心支撑更明确,因此,V型中心支撑的内力最小。
3.4 IDA曲线
增量动力分析(Incremental Dynamic Analysis,IDA)是结构抗震性能分析常用的研究方法,该方法将一条地震动记录分别乘以一系列因子,从而“调幅”为一系列地震动记录,然后在这组“调幅”后记录的地震动作用下求得结构的动力响应,最后通过绘制“调整因子-最大响应”曲线(即IDA曲线)来评估结构的抗震性能。IDA方法目前已被美国联邦应急管理署(FEMA)用来评估结构整体抗倒塌能力。
本文中采用IDA方法,以IDCR为调整因子,以不同IDCR下结构位移时程曲线的位移最大值作为最大响应,绘制出IDA曲线,如图8所示。
由图8可以看出:与Pushdown曲线类似,无支撑框架的IDA曲线在初始阶段时,荷载与位移成比例增加,结构变为弹性,随着荷载的增加,曲线逐渐进入弹塑性阶段;而在有支撑框架的IDA曲线中,结构动力响应的峰值位移与荷载基本呈线性关系,直至结构发生突然破坏。如果将IDA曲线的斜率看作结构“动力响应刚度”,则可以看出,X型中心支撑、V型中心支撑和反V型中心支撑这3种支撑框架的刚度相差不大,而2种偏心支撑的刚度要略低于相应的中心支撑,这是由于耗能梁端的存在引起的,反V型偏心支撑的刚度要略大于V型偏心支撑,但无论何种支撑形式,其刚度都要远大于无支撑框架结构。

图7 无支撑框架轴力时程曲线Fig.7 Axial Force Time History Curves of Unbraced Frame
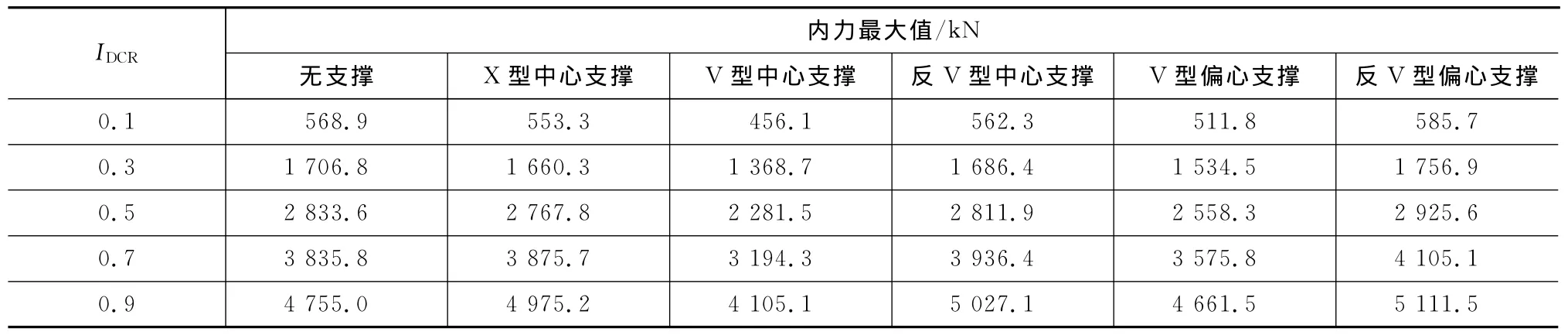
表4 中柱失效后临柱内力最大值Tab.4 Maximum Values of Internal Forces in Adjacent Column After Middle Column Failed
4 结语
(1)无论采用何种形式的支撑,支撑对结构的极限承载力提高并没有太大影响,但对结构刚度提升效果十分明显。无论在承载力还是刚度上,中柱失效结构均要大于边柱失效结构。
(2)无论在底层中柱失效时还是边柱失效时,X型中心支撑、V型中心支撑和反V型中心支撑都可以明显减小失效处节点位移,效果最好;而V型偏心支撑和反V型偏心支撑刚度则相对较小,但在中柱失效时的承载力略有提高。V型支撑在一定程度上会减小临柱内力,而其余形式支撑的设置并不会对临柱内力有太大改变。
(3)总体来说,在框架的抗连续倒塌性能方面,偏心支撑并没有体现出比中心支撑更优越的性能,虽然承载力相差不大,但是会在一定程度上降低框架的刚度。

图8 IDA曲线Fig.8 IDA Curves
[1]ASCE/SEI 7-05,Minimum Design Loads for Buildings and Other Structures[S].
[2]BS 8110-1:1997,Structural Use of Concrete—Part 1:Code of Practice for Design and Construction[S].
[3]EN 1991-1-7:2003,Eurocode 1:Actions on Structures.Part 1-7:General Actions—Accidental Actions[S].
[4]GSA 2003,Progressive Collapse Analysis and Design Guidelines for New Federal Office Buildings and Major Modernization Projects[S].
[5]UFC 4-023-03,Design of Buildings to Resist Progressive Collapse[S].
[6]江晓峰,陈以一.建筑结构连续性倒塌及其控制设计的研究现状[J].土木工程学报,2008,41(6):1-8.
JIANG Xiao-feng,CHEN Yi-yi.A Review on the Progressive Collapse and Control Design of Building Structures[J].China Civil Engineering Journal,2008,41(6):1-8.
[7]易伟建,何庆锋,肖 岩.钢筋混凝土框架结构抗倒塌性能的试验研究[J].建筑结构学报,2007,28(5):104-109,117.
YI Wei-jian,HE Qing-feng,XIAO Yan.Collapse Performance of RC Frame Structure[J].Journal of Building Structures,2007,28(5):104-109,117.
[8]陆新征,李 易,叶列平,等.钢筋混凝土框架结构抗连续倒塌设计方法的研究[J].工程力学,2008,25(增2):150-157.
LU Xin-zheng,LI Yi,YE Lie-ping,et al.Study on Design Method to Resist Progressive Collapse for Reinforced Concrete Frames[J].Engineering Mechanics,2008,25(S2):150-157.
[9]胡晓斌,钱稼茹.单层平面钢框架连续倒塌动力效应分析[J].工程力学,2008,25(6):38-43.
HU Xiao-bin,QIAN Jia-ru.Dynamic Effect Analysis During Progressive Collapse of a Single-story Steel Plane Frame[J].Engineering Mechanics,2008,25(6):38-43.
[10]舒赣平,凤俊敏,陈绍礼.对英国防结构倒塌设计规范中拉结力法的研究[J].钢结构,2009,24(6):51-56.
SHU Gan-ping,FENG Jun-min,CHEN Shao-li.A Study of Tying Force Method in UK Steelwork Design Code[J].Steel Construction,2009,24(6):51-56.
[11]钱稼茹.美国偏心支持框架(EBF)的极限状态设计与实例[J].钢结构,1994,9(3):185-189.
QIAN Jia-ru.Limit-state Design Method in Strength of Eccentric Braced Frame(EBF)and Examples Exercised in USA[J].Steel Construction,1994,9(3):185-189.
[12]舒兴平,沈蒲生.钢框架极限承载力的有限变形理论分析和试验研究[J].工程力学,1993,10(4):32-41.
SHU Xing-ping,SHEN Pu-sheng.Geometrical and Material Nonlinear Analysis of the Ultimate Strength of Steel Frames[J].Engineering Mechanics,1993,10(4):32-41.
