海底浊流在坡道转换处的流动及沉积的数值模拟①

郭彦英 黄河清

(安徽工业大学环境流体研究所 安徽马鞍山 243032)

0 引言

海底浊流形成的浊积岩层为重要的海底油气储层已是国内外学术及产业界的共识［1～7］。近几十年的研究使我们认识到海底浊流为由湍流支持的含有沉积物颗粒的重力流，是将陆源沉积物搬移到海底的重要作用力，地球上最大的沉积为浊流所形成的海底沉积扇和深海平原［1，2］。研究浊流在不同坡度上(比如说大陆架及大陆坡上)的流动及其沉积，会有助于我们理解现有的沉积特征的形成过程及环境，协助探明相关油气储层。

野外观测测量告诉我们海底浊流可由河流入海、风暴及地震等引起的滑塌等作用形成、可在大陆架及大陆坡形成规模巨大的弯曲的类似于陆地河流的海底峡谷，最终在深海坡度平缓处形成巨大海底沉积扇［1～7］。由于坡度的大小决定着海底浊流的侵蚀还是沉积，所以许多实验及数值计算模拟都研究浊流由一接近于大陆坡的坡度(4°左右)的斜坡流入接近于平坡的沉积及流动状况［8～13］。Garcia［7～9］测量了浊流由一5 m长4.8°的斜坡流入约6.6 m长的水平坡的流动速度、浓度及沉积特征，确认了有稳定入流的浊流在平衡状态时的自相似性，即各剖面处的无量纲速度及浓度曲线趋于一致;但对含粗粒沉积物的浊流并未观测到预想中的如明渠流中的急流转变为缓流所发生的水跃及其相应的沉积特征，并推测原因可能是水平渠道不够长。Islam和Imran［11］最近采用新型的声学多普勒测速仪ADV(Acoustic Doppler Velocimeter)重新进行了Garcia的实验，测量了之前未能测量的湍流动能，确认了处于平衡状态的浊流不仅速度及浓度，并且湍流动能也是自相似的。Huang等［12，13］建立了一基于不可压缩流体Navier-Stokes方程和湍流k-ε模型的浊流数值计算的数学模型，并验证可以很好的模拟上述实验浊流的流动及沉积特征并成功再现了水下直峡谷内浊流的外溢及相伴随的自我建堤现象。并且，Huang等［14］通过对水下重力流的断面比能的分析，在研究了海底浊流上边界的水卷吸及底边界的沉积物颗粒的沉积和卷吸后，提出水下浊流的临界密度弗雷德数Frdc(critical densimetric Froude Number)，可以大于1、小于1或不存在。对于斜坡上的海底浊流激流，若其为弱沉积性或弱沉积物卷吸型浊流，水卷吸的影响较大，Frdc＞1，相应的水下水跃如果存在的话，也较弱，其两边沉积物的变化也应相对较小;若水下浊流为含大粒径颗粒的强沉积性的海底浊流，浊流的能量会因沉积而耗散至无需水跃来进一步消耗能量，其Frdc不存在，相应的沉积特性应是渐变的;若其为强沉积物卷吸型的浊流且又遇有反向斜坡时，Frdc＜1，此类水跃跨距最短，强度也高，水跃两边的沉积物会呈现明显的不同特征。这可以很好地解释Garcia实验中对同样的入流，盐水重力流可以观察到水跃，而强沉积型的浊流却没有水跃的现象。

由上述相关研究的概述我们可以看到，有关海底浊流及其沉积的实验及计算模拟研究多为在固定斜坡上的浊流流至平滑的水平坡上的研究。实际的海底峡谷存在着多种坡度转换段，且由边堤溢出的浊流的坡度也在较广的范围内变化。因此研究浊流在较广范围内的斜坡(0.5°～10°)上流至近水平坡的流动及沉积状况的特征，对于我们根据深海沉积扇或峡谷堤外沉积特征反演沉积环境，从而更准确地判断可能的油气储层的状况会有一定的帮助，这正是本文的研究目标。

1 数值计算模型概述

1.1 建模方程

深海里坡度较缓渠道里的浊流由于在其运移过程中经沉积及对环境水体的夹带，其含沉积物浓度一般不高(＜10%)［1，2］，对此类浊流的混合流体可采用不可压缩流体雷诺平均Navier-Stokes(RANS)方程来进行模拟，其质量和动量守恒方程的张量形式如下［7，9，10］:

其中ui是坐标轴xi方向的雷诺平均速度，t为时间，p为压强，ρ和μ分别为液体密度、黏度，μi为涡黏度。考虑到浊流的特殊性，对湍流的模拟采用进行了浮力项修正的标准k-ε模型来模拟湍流动能k及湍流耗散速率ε。涡黏度依下式求得:

沉积物体积比浓度c的传输方程为:

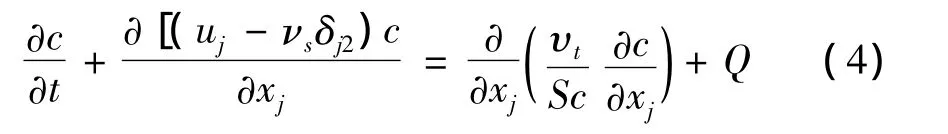
式中νs为沉积物在水中的下沉速度，δ为克罗内克符号，υt为运动涡粘度，Sc为施密特数。本研究中施密特数取1。Q为源项，沉积物和边界的物质交换，包括沉积和夹带，需在此考虑。Huang等利用此模型模拟实验的水下斜坡上盐水重力流及含沉积物的有稳定连续入流的浊流、突然释放型重力流以及三维的梯形直渠道上的浊流的流动及沉积等，均取得了和实验数据相当一致的结果［12～17］，所以本研究中采用与之相同的模型参数来进行研究。

1.2 边界条件

在本研究中，入口需指定流体的流速及各粒径沉积物的浓度，而入口处的湍流动能及耗散率则依经验方程估算［8］。在出口边界，对各变量采取零梯度外延。出口处设定在远离我们需详细研究的区域，以使出口处可能出现的误差对流场的影响尽可能地小。水面采用对称边界条件，这对在深处底部流动的浊流几乎没有影响［13］。对底部边界，假设其粗糙度为入流沉积物的平均粒径值，对流场应用墙面律，对可沉降的泥沙状污染物应用综合的Exner方程以考虑粒状物的沉降、夹带及因底部推移质移动所引起的底部边界的变化。沉积量由模拟的底部沉积物浓度乘以对应的下降速度即可获得，夹带及推移质移动量分别采用了van Rijn及Smith和McLean的基于河床剪切力的经验公式［27～29］。采用这些方法的计算模拟均取得了和实验较为理想的一致［12～17］。

1.3 数值计算方法

采用的数值模拟的基本方法为Ferziger and Peric所描述的适用于非正交网格的有限体积元法［30］。该方法的优点是可使模型方程保持其原始形式且各离散项都有清晰的物理意义，有助于进一步分析和编程。对模型方程的对流项采用近似于二阶精度的中心离散及迎风格式的混合法，扩散项的浓度梯度按具有二次精度的高斯定理计算。对非恒定项采用二阶精度隐式方案。在对守恒方程的各项离散后，任何一个网格单元中心最终的离散方程式可写成一个线性方程式，对整个模拟区域的网格线性离散后即得到一线性方程组。然后应用收敛快的迭代数值求解该线性方程组，求得未知变量。整个建模方程数值求解过程具体如下:(i)根据假定的或上时间步的速度、浓度及压力场解动量方程，求得新的时间步的速度场;(ii)按SIMPLEC算法解含质量守恒的Poison方程，求得压力修正项;(iii)修正压力场及速度场;(iv)解湍流方程(k-ε或其他适用模型)得涡粘度;(v)依解沉积物颗粒的搬运方程;(vi)循环上述过程至此时间步的解收敛;(vii)解埃克森方程求得底部边界的变化及浊流中沉积物和河床的沉积物的交换;(viii)在保持上表面不变的前提下根据底部边界的变动重新分配网格间距;(ix)推进到下一时间步的计算，重复上述步骤，不断推进即可求出浊流在空间及时间上的演化。前期的研究结果表明，上述方法切实可行，对水下盐水重力流、分选差的多粒径组泥沙流及其沉积、水下突然释放型开闸重力流及水下三维直河道的浊流及其沉积的模拟结果均和实验吻合较好［12，13］。

2 计算模型的设立

这里我们讨论正式进行计算模拟实验前的准备工作，包括模拟浊流流入的坡度范围、模拟的空间尺度及计算网格的产生及测试。

2.1 浊流入流及模拟空间的设定

考虑到实际浊流由海底峡谷流入沉积扇以及由峡谷边堤溢出流所能遇到的各种角度范围，初步将模拟入流浊流的坡度设定为在0.5°～10°的范围。其间又分别设定了1°，2°，5°，8°等 4 个角度，所以共要模拟6种不同坡度的入流。浊流流经的沉积扇或溢出堤坝一定距离后的坡度很小，实验室一般用水平坡来模拟。即使初始时是水平坡，浊流沉积开始后，沉积物本身也会建立起一小坡度，所以我们初始即假设上述斜坡上的入流均流入一坡度为0.01的近似的水平坡上。根据Xu(2004)等的对实际浊流的观察，浊流的流速可达2 m/s，厚度达几十米。按几何尺度1∶100缩小，保持模型和原型的弗雷德数一致，模拟的入流速度设定为0.15 m/s，厚度为0.05 m。计算模型的斜坡长6 m，后续近似水平坡长14 m。之所以采取这一模拟尺度，是因为所采用的数学模型被证明可以很好地模拟此尺度下一系列浊流实验［32］。另假设浊流所含沉积物的体积比浓度为0.02，比重为2.65，粒径为25 μm，设周边海水的密度为1 000 kg/m3，这样浊流入流的密度为1 033 kg/m3。自然界中虽然不存在单一粒径的沉积物，但通过模拟含平均粒径沉积物的简化的模型的沉积特性，其结果可以大致反映自然界中复杂的多粒径沉积物的一些沉积特性。

2.2 网格的产生及测试

将原型长2 000 m，深约100 m的峡谷按1∶100比例产生计算用网格如图1所示。网格对底部进行了加密以期能较为准确地模拟浊流底部的边界层。

数值模拟重要的一步是需确认模拟的结果不会因网格密度的改变而改变，一般是通过比较加倍网格密度所模拟的结果来进行。我们对5°斜坡的网格进行了密度加倍的模拟确认。采用130×60的网格所模拟结果和加倍网格密度所模拟的结果几乎一致，即模拟的结果是可靠的。下面模拟实验中采用了此密度的网格。

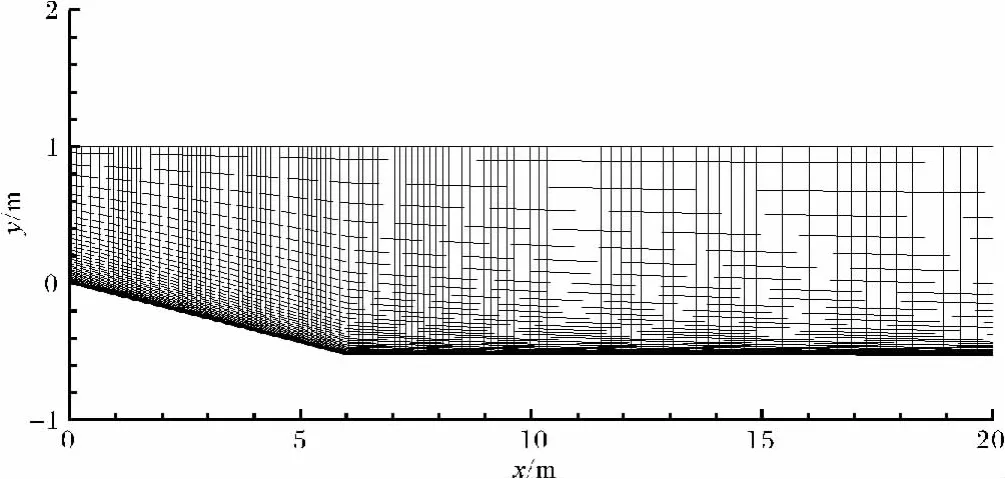
图1 计算模拟用网格图Fig.1 Grid for the simulation domain

3 模拟结果及分析

这节我们将从密度云图及速度矢量、浊流厚度、深度平均速度及浓度、沉积厚度及粒度分布等方面来具体分析坡度对海底浊流的流动及沉积的影响。

3.1 密度云图及速度矢量

水下浊流的二维纵向解析的数值模拟可以向我们展示如同观察实验一样的模拟效果。图2为浊流由不同坡度入流200 s后的密度云图及速度矢量图。

由图可见，随着入流坡度的增大，

(1)斜坡上流速明显增大;

(2)浊流在后续相同水平坡上的流速也一定程度地承接了上游坡上的流速，有一些增大趋势，但没有坡上流速随坡度增大而增大那么明显;

(3)水夹带系数也随坡度的增大而增大，表现在密度云图所反映的浊流厚度在斜坡上随坡度增大而更加快速地沿下游方向变厚，这和Ellison和Turner(1959)年早期的水下重力流的实验观察是一致的［31］;

(4)随着上游坡度的增大，下游水平坡上的浊流也明显地呈现渐次增厚。

3.2 浊流深度及深度平均速度和浓度

浊流深度、深度平均速度及浓度可由下面的积分式(5 ～7)求得［31］。

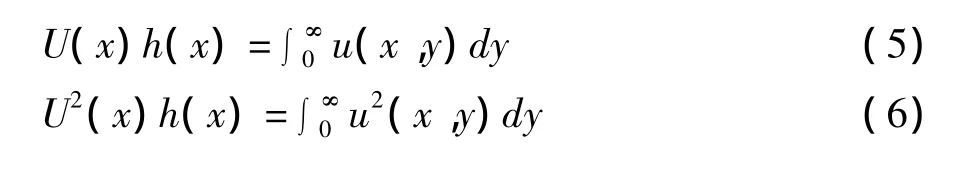
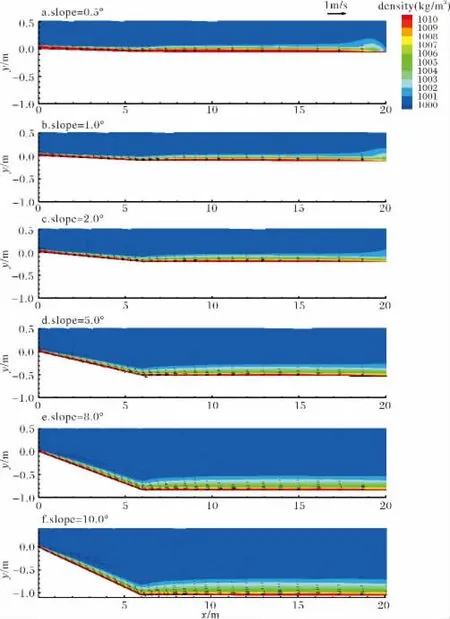
图2 浊流由左下入口流入后200 s的浊流密度云图及速度矢量图Fig.2 The density contours and velocity vectors of turbidity currents at 200 s after inflow initiated on different slope beds

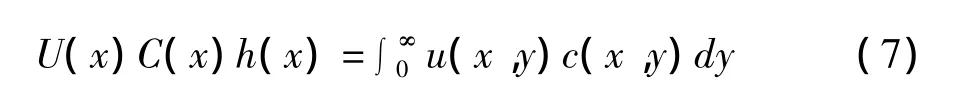
式中y为纵剖面上至谷底距离，实际积分时只需至速度足够小的高度即可。式(6)除以式(5)即得深度平均速度U，式(5)除以U即得浊流深度h，式(7)除以Uh即得深度平均浓度。按上述方法求得的模拟浊流的各变量变化情况如图3所示。由图可见:

(1)在斜坡上，浊流厚度随着坡度的增加而更加快速地增厚，这是由于浊流的水夹带系数随着坡度的增加而增加的缘故;

(2)而在水平坡上，浊流厚度在斜坡末端厚度的基础上以几乎相同的速率沿下游方向缓慢增长，反映了浊流的水夹带系数可能是坡度的函数，只要坡度一定，不论流速及浓度的变化，其厚度增长率都是相同的;

(3)斜坡上的浊流流速随着坡度的增加而增加，至水平坡时，速度会有一定的下降，坡度变换的差别越大，下降幅度也越大，但不会低于小于其坡度的同样浊流的转换后的速度;

(4)在斜坡上，入流浊流的浓度随着坡度的增加而更加快速地下降，这也反映了水夹带程度随着坡度的增加而增加。坡度增加，更多的周边水体被卷吸进浊流，从而引起浓度更快地降低。

(5)至相同水平段后，浓度的下降幅度渐渐趋于平缓，大坡度(10°，8°)入流的浊流在12 m之后比小坡度的浓度更高。这可能是因为大坡度入流的流速快，形成的湍流强度大，搬运能力强，沉积也相应较少(图4e，f)，使浊流中保留了较多的沉积物，其作用大于水夹带的稀释作用，因而，在下游一定距离内形成了相对较高的浓度。

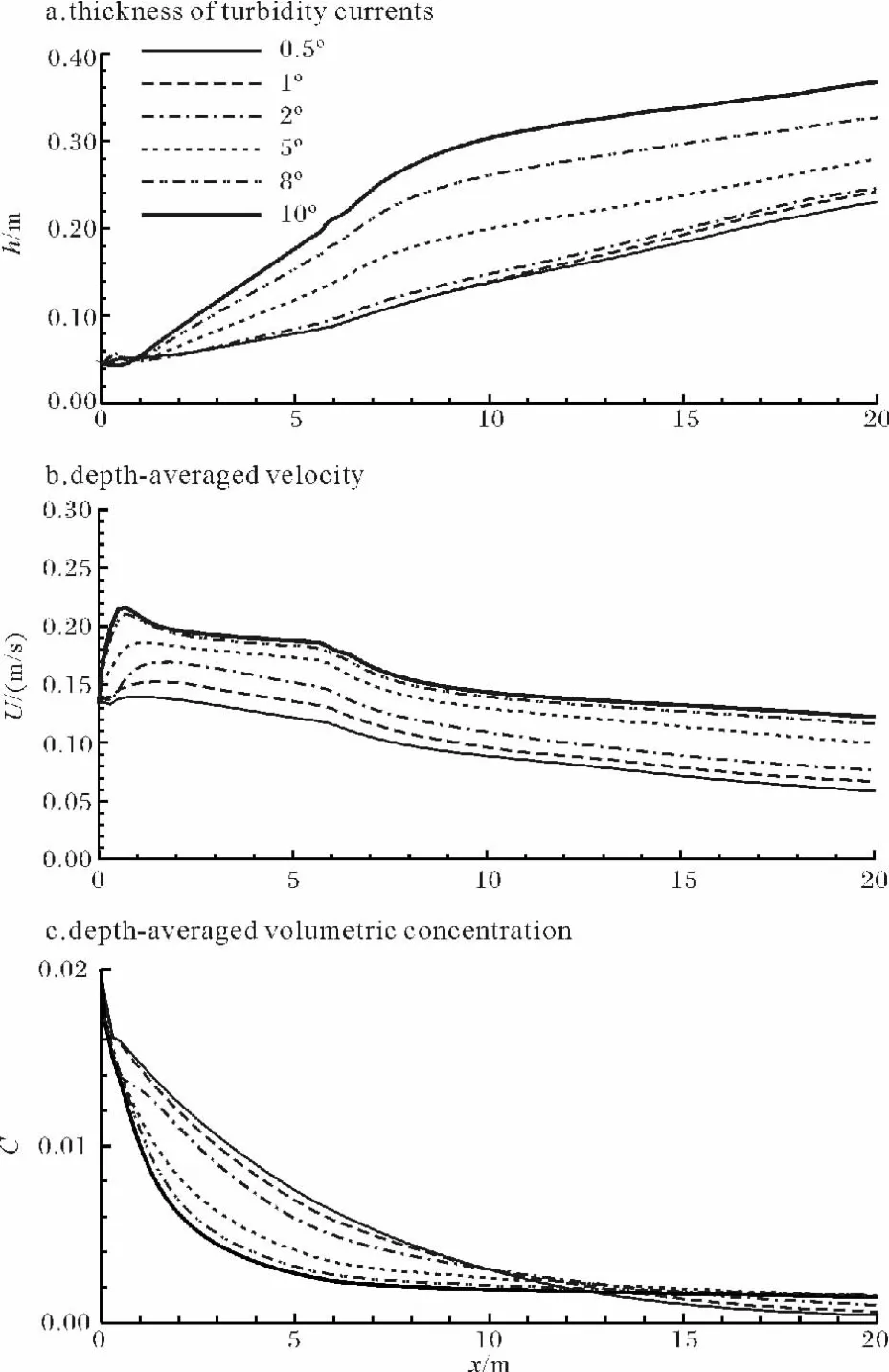
图3 不同坡入流浊流的(a)厚度、(b)深度平均速度及(c)深度平均浓度图Fig.3 The thickness(a)，depth-averaged velocity(b)and depth-averaged concentration(c)of turbidity currents from different inflow slopes

3.3 沉积厚度分布

5次相同的浊流入流流动1 000 s，沿着6种不同坡度及在水平坡因沉积或侵蚀所引起的地形变化如图4所示。由图可见:

(1)当坡度很小时(＜2°)，沉积会渐渐覆盖原有的坡度变化，形成一新的较大的坡度;

(2)当坡度≤2°时，在斜坡上的沉积厚度大于近似水平坡上的沉积;

(3)当坡度大于2°但小于9°时，坡下沉积物厚度大于坡上沉积;

(4)当坡度为8°时，坡上几乎没有沉积，意味着此坡度时沉积和夹带处于平衡状态;

(5)当坡度＞8°时，在斜坡上为侵蚀状态，坡度转换处沉积明显减少，其后渐渐增多，形似长波长的沉积物波。

坡度较大时，水平坡上沉积物少的原因可能是较高的流速将更多的沉积物带至了下游。

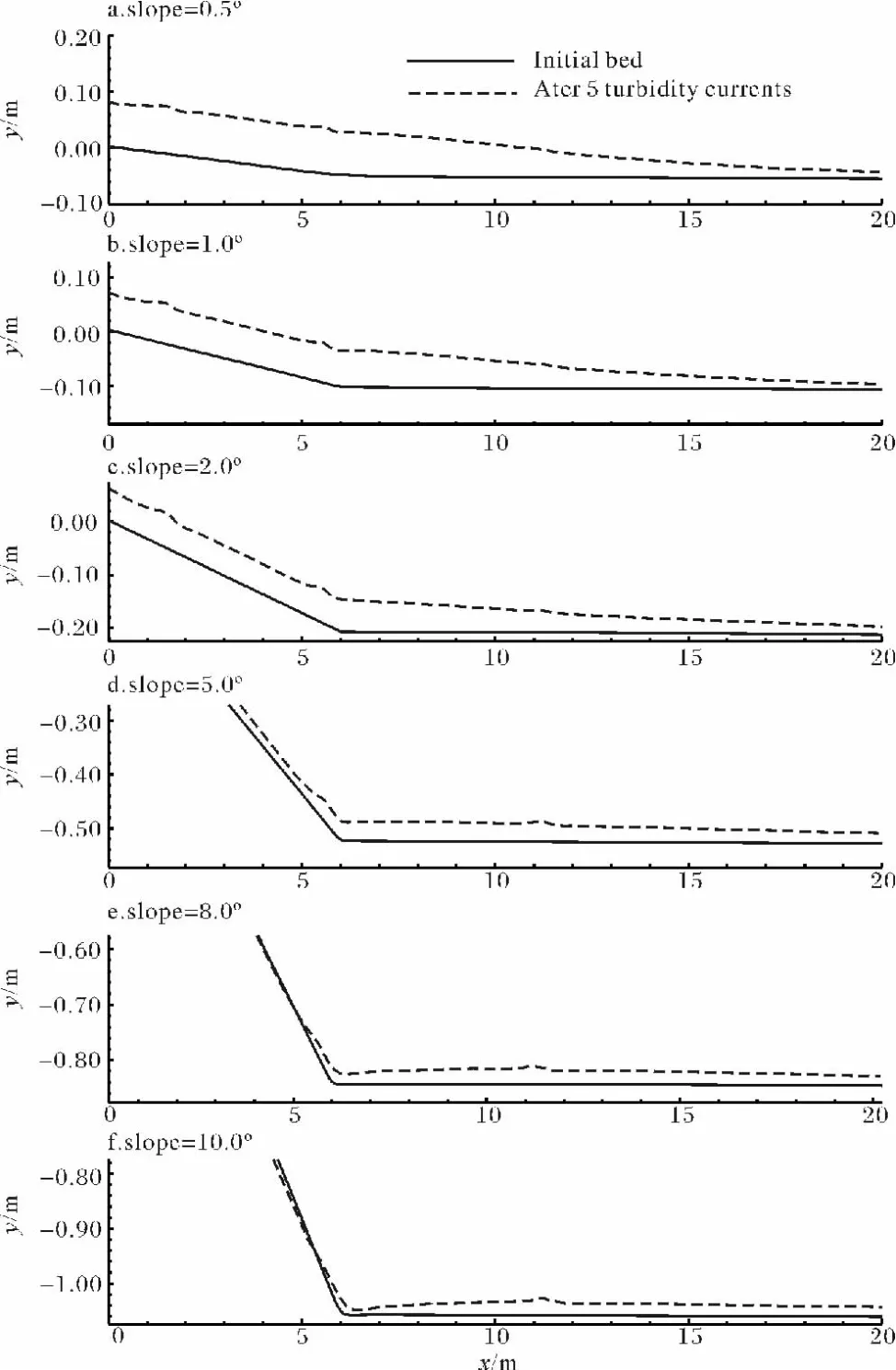
图4 不同坡度入流的5次浊流事件的沉积厚度Fig.4 Bed deformation after five turbidity current events with different inflow slopes

Kubo和Nakjima(2002)通过浊流的二维深度平均模型模拟多粒径沉积物的浊流的多次沉积事件，得出沉积物波可以通过多次的浊流事件在坡度转换处先形成一个波，在通过后续的多次浊流事件向上迁移即形成更多的波，而单粒径沉积物构成的浊流难以形成沉积物波［32］，我们今后将继续探讨这个问题。

4 结论

基于不可压缩流体的RANS方程和湍流k-ε模型建立了含沉积物的重力流的三维动力学模型。应用此模型模拟了相同入流的单粒径沉积物构成的浊流由不同坡度流入近似水平坡的流动及沉积特征，得出如下主要结论:

(1)浊流在斜坡上经短距离调整适应后的平衡状态下的流速随着坡度的增大而增大;在坡度突然转低处，坡度变化的程度越高，速度下降幅度也越大，完成下降的空间跨度也越短;但在相同的水平坡度段，上游坡度越大的话，在水平坡上的流速也相对较高。

(2)由浊流厚度所反映的浊流的水夹带系数是坡度的函数，坡度越大，水夹带系数也越高，反映在浊流厚度在斜坡上线性增长的速率越快，而在下游相同的水平坡上，不同上游斜坡流来的浊流厚度随距离增长的速率趋于一致，反映了坡度对水夹带的较强的控制作用。

(3)和水夹带系数相关的是，浊流浓度在坡度较大的坡上因水夹带系数较大以更快的速率下降，而在相同的水平坡上下降速率趋缓。

(4)在沉积方面，当坡度较小时，坡上沉积多，坡下少，沉积会渐渐覆盖原有的坡度变化，形成一新的较大的坡度;

(5)存在一个临界坡度，当斜坡坡度小于临界坡度时，斜坡上为沉积，坡度越小，沉积越多;随着坡度渐渐增大坡上沉积渐渐减少;过了临界坡度之后，斜坡显示侵蚀现象，使坡度趋于渐渐减小，在坡度转换处沉积明显减少，其后渐渐增多，形似长波长的沉积物波。对于所模拟的粒径为25 μm沉积物来说，此临界坡度为8°左右。

要注意上述模拟结果依赖于我们所采用的依据实验所得河床推移质搬运及河床沉积物颗粒的临界启动剪切力的经验公式等，改变了这些及沉积物颗粒粒径的话，模拟的结果会有一定的改变，但基本特征应相同。了解了不同坡度转换的浊流沉积的上述特点，对于我们根据实测的浊流沉积的剖面特征推测其形成的环境，进而推测相关油气储层的分布状况可能会有一定的参考作用。

References)

1 Middleton G V.Sediment deposition from turbidity currents［J］.Ann.Rev.Earth Planet of Science，1993，21:89-114

2 Kneller B，Buckee C.Turbidity Currents and their deposits［J］.Ann.Rev.Fluid Mech，2010，42:135-156

3 Kneller B，Buckee C.The structure and fluid mechanics of turbidity currents:A review of some recent studies and their geological implications［J］.Sedimentology，2000，47:62-94

4 孙枢.中国沉积学的今后发展:若干思考与建议［J］.地学前缘，2005，12(2):3-10［Sun Shu.Sedimentology in China:Perspectives and suggestions［J］.Earth Science Frontiers，2005，12(2):3-10］

5 方爱民，李继亮，侯泉林，等.浊流及相关重力流沉积研究综述［J］. 地质论评，1998，33(3):384［Fang Aimin，Li Jiliang，Hou Quanlin，et al.Sedimentation of tuibidity currents and relative gravity flows:A review［J］.Geological Review，1998，33(3):384

6 Shanmugan G，Moiola R J.Submarine Fans and Related Turbidite Systems［C］.Bouma A H，Normark W R，Barns N E，eds.Springer-Verlag，New York，1985:29-34

7 Garcia M，Parker G.Experiments on hydraulic jumps in turbidity currents near a canyon-fan transition［J］.Science，1989，245:393-396

8 Garcia M.Hydraulic jumps in sediment-driven bottom currents［J］.Journal of Hydraulic Engineering，1993，119(10):1094-1117

9 García M.Depositing and eroding turbidity sediment driven flows:Turbidity Currents［C］，Project Report.306，St.Anthony Falls Hydraulic Laboratory University of Minnesota，Minneapolis，1990

10 Choi S，Garcia M H.k-ε turbulence modeling of density currents developing two dimensionally on a slope［J］.Journal of Hydraulic Engineering，2002，128(1):55-63

11 Islam M A，Imran J.Vertical structure of continuous release salineand turbidity currents［J］.Journal of Geophysical Research，2010，115:1-14

12 Huang H，Imran J，Pirmez C H.Numerical model of turbidity currents with a deforming bottom boundary［J］.Journal of Hydraulic Engineering，2005，131(4):283-293

13 Huang H，Imran J，Pirmez C.Numerical modeling of poorly sorted depositional turbidity currents［J］.Journal of Geophysical Research，2007，112:1-15

14 Huang H，Imran J，Pirmez C，et al.The critical densimetric froude number of subaqueous non-unity or non-existent［J］.Journal of Sedimentary Research，2009，79(7-8):479-486

15 Huang H，Imran J，Pirmez C.Numerical study of turbidity currents with sudden-release and sustained-inflow mechanisms［J］.Journal of Hydraulic Engineering，2008，134(9):1199-1209

16 Huang H，Imran J，Pirmez C.Nondimensional Parameters of depthaveraged gravity flow models［J］.Journal of Hydraulic Research，2009，47(4):455-465

17 Huang H，Imran J，Pirmez C.The depositional characteristics of turbidity currents in submarine sinuous channels［J］.Marine Geology，2012，329-331:93-102

18 李华，何幼斌，王振奇.深水高弯度水道—堤岸沉积体系形态及特征［J］. 古地理学报，2011，13(2):139-149［Li Hua，He Youbin，Wang Zhenqi.Morphology and characteristics of deep water high sinuous channel-levee system［J］.Journal of Palaeogeography，2011，13(2):139-149］

19 赵月霞，刘保华，李西双，等.东海陆坡海底峡谷—扇体系沉积特征及物质搬运［J］.古地理学报，2011，13(1):119-126［Zhao Yuexia，Liu Baohua，Li Xishuang，et al.Sedimentary characters and material transportation of submarine canyon-fan systems in slope of the East China Sea［J］.Journal of Palaeogeography，2011，13(1):119-126］

20 丁巍伟，李家彪，韩喜球，等.南海东北部海底沉积物波的形态、粒度特征及物源、成因分析［J］.海洋学报，2010，32(2):96-105［Ding Weiwei，Li Jiabiao，Han Xiqiu，et al.Geomorphology，grainsize characteristics，matter source and forming mechanism of sediment waves on the ocean bottom of the northeast South China Sea［J］.Acta Oceanologica Sinica，2010，32(2):96-105］

21 韩喜彬，李家彪，龙江平，等.我国海底峡谷研究进展［J］.海洋地质动态，2010，26(2):41-48［Han Xibin，Li Jiabiao，Long Jiangping，et al.Development of research on submarine canyon in China［J］.Marine Geology Letters，2010，26(2):41-48］

22 汪品先.深海沉积与地球系统［J］.海洋地质与第四纪地质，2009，29(4):1-11［Wang Pinxian.Deep sea sediments and earth system［J］.Marine Geology ＆ Quaternary Geology，2009，29(4):1-11］

23 李祥辉，王成善，金玮，等.深海沉积理论发展及其在油气勘探中的意义［J］. 沉积学报，2009，27(1):77-86［Li Xianghui，Wang Chengshan，Jin Wei，et al.A review on deep-sea sedimentation theory:significances to oil-gas exploration［J］.Acta Sedimentologica Sinica，2009，27(1):77-86］

24 韩小锋，陈世悦，牛海青.海相深水沉积研究现状及展望［J］.地质找矿论丛，2008，23(4):275-280［Han Xiaofeng，Chen Shiyue，Niu Haiqing.The present research status of deep-water deposition and forecasts［J］.Contributions to Geology and Mineral Resources Research，2008，23(4):275-280］

25 陈海洲，李瑞军.深水浊积砂体的成因机理及特征［J］.上海地质，2007，(3):10-13［Chen Haizhou，Li Ruijun.The characteristic and genesis mechanism of deep water turbidity sandbodies［J］.Shanghai Geology，2007，(3):10-13］

26 王海荣，王英民，邱燕，等.南海北部大陆边缘深水环境的沉积物波［J］. 自然科学进展，2007，17(9):1235-1243［Wang Hairong，Wang Yingmin，Qiu Yan，et al.The sediment-wave in the deep-water environment of continental margin of the north of South China Sea［J］.Process in Nature Science，2007，17(9):1235-1243］

27 Felix M.A two-dimensional numerical model for a turbidity current［J］，Spec.Publs.int.Ass.Sediment，2001，31:71-81

28 Smith J D，McLean S R.Spatially averaged flow over a wavy surface［J］.Journal of Geophysical Research，1977，82(12):1735-1746

29 Van Rijn L C.Sediment transport，Part I:bedload transport［J］.Journal of Hydraulic Engineering，1982，110:1431-1456

30 Ferziger J H，Peric M.Computational methods for fluid dynamics(2nd Edition)［M］.New York:Springer，1999

31 Ellison T H，Turner J S.Turbulent entrainment in stratified flows［J］.Journal of Fluid Mech.，1959，6:423-448

32 Kubo Y，Nakajima T.Laboratory experiments and numerical simulation of sediment-wave formation by turbidity currents［J］.Marine Geology，2002，192:105-121