土石坝渗流的流固耦合方法计算分析
2013-12-07代凌辉杨卫元
代凌辉,张 玓,杨卫元
(1.黄河水利职业技术学院,河南 开封 475004;2.鹤庆县水利水电勘测设计队,云南 鹤庆 671500)
0 引言
在土石坝的设计中,渗流问题对坝体的稳定性至关重要,也极大地影响着构筑物的安全和造价。 在进行排水和防渗设施设计或进行坝体稳定性计算时,一般都需要先确定出渗流的自由面[1~2]。 在目前的分析方法中,由于有限元方法能够有效地处理复杂的边界条件、材料的非均匀性、材料的各向异性,并能方便地求解三维问题,在工程设计中被广泛使用。 传统的渗流有限元求解方法的难点是自由面(浸润面)的位置确定,因为渗流区域是未知的,需要通过迭代求解。 使用变网格迭代法,在每次迭代计算时,都要确定自由面的位置,并根据自由面的位置调整渗流网格。 这样,在计算过程中,不但需要重新形成和分解总体传导矩阵,耗费大量的计算时间,而且在自由面附近的单元也可能出现畸形,使得求解失真[3~4]。 目前,许多研究者采用固定网格的方法进行研究。 该方法按照非饱和土力学理论,将整个区域作为分析区域,浸润面取孔隙水压力为零的地方,为问题的求解提供了很大的便利,并保证了较高的精度[5]。 本文试采用基于固定网格的有限元流固耦合法进行分析。
流固耦合是研究变形固体在流场作用下的各种行为,以及固体位行对流场影响的一种计算方法,其重要特征是两相介质之间的相互作用。 变形固体在流体载荷作用下会产生变形或运动,变形或运动又反过来影响渗流,从而改变流体载荷的分布和大小。
1 土石坝非饱和渗流的典型边界条件
土石坝非饱和渗流在进行流固耦合计算时的典型边界条件如图1 所示。 其各边的边界条件为[5]:(1)S1是上游坝面水位以下部分,边界条件为上游已知总水头(此处的总水头等于H1)。在进行有限元流固耦合分析时,只需给出边界上的孔隙水压力即可。 (2)S2是下游坝面水位以下部分,边界条件为下游已知总水头(此处的总水头等于H2)。 同样,在进行有限元流固耦合分析时,只需要给出边界上的孔隙水压力。 (3)S3是坝基不透水基岩,为不透水边界条件,通过该边界的流量为零。 (4)S4为浸润线,其位置是未知的。 该边界上孔隙水压力为零,即总水头等于位置水头z。 在传统的渗流分析中,将该面也看成不透水边界,即渗流只在饱和区内发生,浸润面是最上方的流线。 但在非饱和渗流分析中,无须如此设置。 (5)S5为自由渗出段边界,孔隙水压力为零,且渗流只能沿着下游坡面进行。 在有限元软件中,该种边界条件只允许孔隙水从分析区域中流出,而不允许水流进入。 即假设当边界面上的孔隙水压力为正时,孔隙流体的流速与孔隙水压力成正比;当孔隙水压力为负值(吸力)时,流速限定为零,即流体不会进入到分析区域内部。 具体表达式为:

式中:vn为渗流流速,ks为渗流系数,uw为孔隙水压力。

图1 土石坝非饱和渗流典型边界条件Fig.1 Unsaturated seepage typical boundary conditions of earth dam
2 土石坝流固耦合计算
2.1 均质土石坝流固耦合计算
某均质土石坝坝高为15 m,坝顶宽度为4 m,上、下游坡比均为1∶2,坝底长度为64 m,上游水位高出建基面13 m,下游水位与建基面平齐。 坝壳料土体的渗透系数为1.0×10-7m/s。 建立有限元模型,共划分306 个节点、272 个单元。 按照非饱和渗流典型边界条件,赋予有限元模型相应的边界条件。 计算完成后,绘制孔隙水压力等值线图(如图2 所示)。 从计算结果中提取迎水面上各节点的渗透流量值,相加之后得到该计算模型的渗透流量,为2.55×10-7m3/(s·m)。 该值与水力学方法得到的结果相比,相对误差小于2%,由此证明流固耦合方法的计算结果比较准确。 从孔隙水压力等值线图中可以得出,孔隙水压力为0 的线即为浸润线,渗流逸出点的位置位于下游坝坡6 m 高处(如图2 所示)。

图2 均质坝算例孔隙水压力等值线图(单位:kPa)Fig.2 Pore water pressures isoline of the homogeneous dam (Unit: kPa)
2.2 黏土心墙土石坝流固耦合计算
某黏土心墙土石坝坝高为127.5 m,坝顶宽为11 m,上游边坡系数为1∶2,下游边坡系数为1∶1.75,上游围堰高为40 m,下游排水棱体高为30 m。 以建基面为相对0 高程面,上游水位117.5 m,下游水位10 m。 黏土心墙顶高程与坝顶高程一致,心墙顶宽11 m,底宽87.5 m。坝体的断面如图3 所示。坝体各分区的渗透系数见表1。 采用有限元流固耦合方法进行计算和分析,建立有限元模型,共划分1 062 个节点,975 个单元。 按照非饱和渗流典型边界条件,赋予有限元模型相应的边界条件。
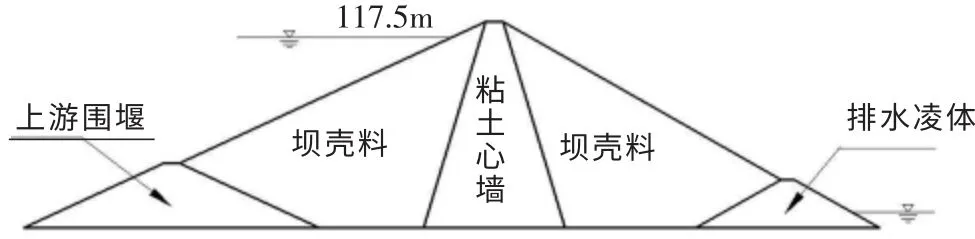
图3 黏土心墙坝横断面图Fig.3 Cross-section of the clay core wall dam

表1 黏土心墙坝算例各分区的渗透系数Table 1 Permeability coefficients of each partition of the clay core wall dam
计算完成后,绘制该黏土心墙坝的孔隙水压力等值线图(如图4 所示)。 从计算结果中提取迎水面上各节点的渗透流量值,相加之后,得到该计算模型的渗透流量,为5.19×10-6m3/(s·m)。从孔隙水压力等值线图可以得出,孔隙水压力为0 的线为浸润线。孔隙水压力等值线在黏土心墙部位急剧下降,说明该坝的黏土心墙防渗效果明显。由此结果可以得出,对于坝体有不同分区、渗透系数不同的非均质坝,有限元流固耦合方法依然适用,而且便捷、高效、结果准确。

图4 黏土心墙坝孔隙水压力等值线图(单位:kPa)Fig.4 Pore water pressures isoline of the clay core wall dam (Unit: kPa)
3 结语
通过对两个算例进行计算,主要得出以下结论:(1) 赋予有限元模型正确的边界条件是得出准确结果的前提。(2)把计算结果中土石坝迎水面上各节点的渗透流量值相加,可得出土石坝整体的渗透流量。(3)根据计算结果,可以绘制出土石坝的孔隙水压力等值线图。 图中,孔隙水压力为0 的线即为浸润线。对于下游逸出点高于下游水位的情况,还可由此确定逸出点的位置。 (4)对于坝体有不同分区、渗透系数不同的非均质坝(如黏土心墙坝),有限元流固耦合方法依然适用,而且便捷、高效、结果较准确。非均质坝的孔隙水压力等值线会在心墙部位急剧下降,由此为检验心墙设计方案的合理性提供了方法和依据。
本文结果证明了采用有限元流固耦合方法计算土石坝非饱和渗流问题的可行性,可为相关类似工程的分析提供参考和借鉴。
[1] 金生,耿艳芬,王志力. 利用饱和-非饱和渗流模型计算坝体自由面渗流 [J]. 大连理工大学学报,2004,44(1):110-113.
[2] 牛文杰,叶为民. 不透水地基上均质土坝渗流自由面的有限元计算[J] .岩土力学,2007(增刊):375-378.
[3] 徐千军,张建红. 确定稳定渗流自由面位置的一种简便方法[J]. 水动力学研究与进展,1999, 14(4):418-423.
[4] 殷宗泽. 土工原理[M]. 北京:中国水利水电出版社,2007:171-189.
[5] 费康,张建伟. ABAQUS 在岩土工程中的应用[M]. 北京:中国水利水电出版社,2010:205-206.
