GF(2m)域上II型最优正规基的字级乘法器

倪 乐，陈 韬，戴紫彬，李 淼

(信息工程大学，河南 郑州 450004)

近些年来，随着椭圆曲线密码体制应用的发展，有限域运算的硬件实现方法成为了研究的热点。由于有限域中正规基[1]上平方运算的易于实现性，正规基被广泛用于表达二进制域上的元素。

本文主要研究正规基上的运算，在正规基中有两种最高效的表示方式，一种是I型最优正规基，一种是II型最优正规基。在 ANSI X9.62[2]和ANSI X9.63[3]中规定了有限域上的元素以正规基表示时的选取规则。但出于安全角度的考虑，I型最优正规基已被许多安全标准排除在外，如 NIST ECDSA和 ANSI X9.62；而 II型正规基由于其更好的安全特性，被广泛推荐及使用在密码算法应用设计中去。本文提出了一种新型基于字级结构的II型正规基乘法器。其特点是关键路径与分割字数及字段大小无关，并可达到很高的时钟频率。

1 II型最优正规基及重序正规基

在 m∈[2，1 000]内，有 155个 m值是存在 II型最优正规基的。II型最优正规基下的乘法矩阵M中1的个数最少，为2m-1个，除第一列外，其他每一列只有两个1，这样就大大降低了乘法运算的空间复杂度和时间复杂度。因此设计针对II型最优正规基的乘法器具有非常重要的意义。

假设β是GF(2)上次数为m的不可约多项式f(x)(正规多项式)的根。如果集合 N={β，β2，β22，…，β2m-1

}中的元素是互相线性无关的，则集合N是扩域GF(2m)上的一组正规基。通过寻找正规多项式，可以建立GF(2)上的扩域GF(2m)的正规基。

定理1[4]令GF(2m)是含2m个元素的有限域。如果2m+1是素数，且下面两个条件之一成立：

(1)2是模2m+1的原根；

(2)2m+1是模4为3的一个素数，并且2模2m+1的次数为m。

则 β=γ+γ-1生成一个 GF(2m)到 GF(2)上的一组最优正规基，其中γ是(2m+1)次本原单位根。

记M为新生成的一组正规基：

则称m为GF(2m)到GF(2)上的一组II型最优正规基。

[5]可得 ，基 M={γ1，γ2，… ，γm-1，γm}为 正222m-1规基 N={β，β2，β ，…，β}的另一种排序形式，M与N之间a′j与 ai角标的映射关系由参考文献[6]中推导出，如下所示：

2 重序正规基字级乘法器设计

2.1 新型字级重序正规基乘法算法

对于任意 A、B∈GF(2m)及其乘积 C∈GF(2m)，均为重序正规基M上表示的数。

则C的单比特ci由以下公式得出：

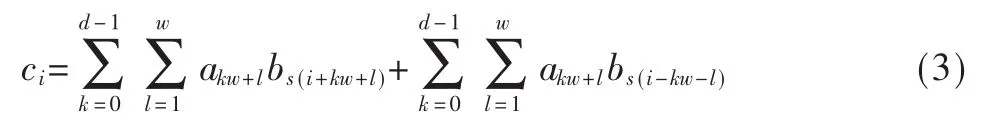
可推出：

综合式(3)、式(4)和式(5)，可得：

由式(6)可推出一种新型字级重序正规基模乘最优算法。

算法1新型字级重序正规基乘法算法

输 入 ：A=(a1，… ，am)、B=(b1，… ，bm)∈GF(2m)，d 为 分割字数，1≤d≤m

输出：C=A×B=(c1，…，cm)∈GF(2m)

②for i=1，2，…，m

④ for l=1，2，…，w，

⑦ end

⑨ end

⑩ end

由以上可得出重序正规基字级乘法器的结构，算法1中的运算均为单比特。在算法第⑤步中，加法用一个XOR门来实现，乘法用一个AND门来实现，而需要一个触发器来保持上一个状态的临时变量。操作数A由外部存储输入，操作数B则需要存入一个(2m+1)bit循环移位寄存器。其中，在l个时钟状态中，函数s(.)的变化规律由bs(i+kw+l)和bs(i-kw-l)决定，如式(7)所示 ：

由上式可推出算法中bs(i+kw+l)和bs(i-kw-l)的下标，并由两个寄存器组成，一个为R1：

另一个为R2：

由公式可知，R1与R2其实为一个寄存器，设计乘法器时将其作为一个(2m+1)bit的寄存器来使用。

2.2 GF(2m)域上重序正规基字级乘法器设计

根据算法1，可以设计出一种 GF(2m)域上新型基于字级结构的重序基乘法器，如图1所示。

图1 GF(2m)域上重序正规基字级乘法器

从图1中可以看出，该乘法器结构由一个(2m+1)bit的循环移位寄存器、连线扩散网络、一层与门、一层累加单元（该单元由一个“异或”门和一个触发器组成）以及一层“异或”阵列组成。其中每一路的核心单元为操作数B的 2 bit相加(“异或”运算)后生成 1 bit，然后再与 1 bit操作数A进行相乘（与运算）得出1 bit部分积，最后部分积反馈到累加单元从而完成一个时钟周期的运算。在经过w+d(d=「m/w-1)个时钟周期后累加单元里的值通过“异或”网络生成最终1 bit的ci值。根据以上分析及图1中的结构，表1中列出了新型字级重序正规基乘法器的空间复杂度。

由于乘积C在经过w个时钟周期后还需要经过“异或”阵列的延迟之后输出有效。这额外的延迟Tex=「log2dTX。 综上所述，总的时钟周期数为

表1 新型字级重序正规基乘法器空间复杂度

3 性能分析与比较

3.1 性能分析

通过前文分析，对于GF(2m)上的模乘运算，该乘法器需要个时钟周期。电路中“与门”个数为dm，“异或”门个数为2dm，空间复杂度为dm#AND+2dm#XOR，时间复杂度为TA+2TX。将本设计与参考文献[7]中的设计进行比较，电路面积对比如表2所示。可以看出，参考文献[7]的设计所占用的电路面积要大于本文中的设计。

表2 不同字级模乘器之间的下复杂度比较

在表2中，与参考文献[8]中的Massey-Omura型乘法器设计相比，本设计采用字级并行结构以后，空间复杂度和时间复杂度均明显降低，这表明电路的时钟频率更高，在花费相同运算时钟周期数的条件下，运算速度更快。

3.2 综合结果

在对GF(2233)上的该型正规基乘法器进行仿真验证后，利用Synopsys公司的Design Compiler工具在0.18μm CMOS工艺标准单元库下对设计进行综合，表3给出了d=8时，4.0 ns约束下的综合报告。

表3 在0.18μm CMOS工艺标准单元库下的综合结果

本文设计了一种支持II型最优正规基的字级乘法算法，针对II型最优正规基与重序正规基之间的特点，给出了基转换方法，设计了一种新的支持II型最优正规基的字级乘法器。根据以上的分析和比较，本文设计的II型最优正规基乘法器在运算速度以及面积等方面具有优势，与串行结构的传统正规基乘法器相比，在GF(2m)上的乘法运算效率得到显著的提高；与全并行结构的传统正规基乘法器相比，大大减少了电路面积；其关键路径延迟与域元素字长无关，能够满足公钥密码中处理高速性和灵活性的要求。

参考文献

[1]WILSON R M．Optimal normal bases in GF(pn)[J]．Discrete Applied Mathematics，1988，89(22)：149-161．

[2]ANSI X9-62.Public key cryptography for the financial service industry-the elliptic curve digital signature algorithm(ECDSA)[S].1999.

[3]ANSI X9-63.Public key cryptography for the financial service industry-the elliptic curve key agreement and apparatus for finite field arithmetic[S].2000.

[4]MULLIN R C，WILSON R M.Optimal normal bases in GF(pn)[J].Discrete Applied Math，1989(22)149-161.

[5]GAO S，VANSTONE S.On orders of optimal normal basis generators[J].Math.Computation，1995，64(2)：1227-1233.

[6]WU H，HASAN M A，BLAKE I F，et al.Finite field multiplier using redundant representation[J].IEEE Trans.Computers，2002，51(11)：1306-1316.

[7]NAMIN A H，Wu Huapeng，AHMADI M.A high speed word level finite field multiplier using reordered normal basis[C].IEEE International Symposium on Circuits and Systems，Seattle，2008.

[8]MASOLEH A R，HASAN A.Low complexity word-level sequential normal basis multipliers[J].IEEE Transactions on Computers，2005，54(2)：98-109.