集成预测模型预测我国农业自然灾害的探讨

王正辉，孙会霞，郭 庆

(1.防空兵学院，河南郑州 450052;2.河南工业大学，河南郑州 450052;3.河南农业大学，河南郑州 450052)

我国是一个农业大国，也是世界上农业自然灾害较为严重的国家之一。农业自然灾害主要包括水灾、旱灾、风灾、虫灾、冻灾等。建国60年来，我国平均每年发生重大水灾、旱灾、风灾等自然灾害23.2次，全国农业每年平均有0.4亿hm2农作物、2亿多人口受灾，经济损失达数百亿元。因此预测农业自然灾害十分必要。

1 预测模型构成

灾害的准确预测是农业的可持续发展条件之一，是灾害防御决策的重要环节。据我国1950-2007年受灾面积统计数据，绘制受灾面积的折线图 (图1)，从图中可见我国农业受灾面积变化既有不断增长的趋势，又有周期变化的规律，还有随机波动成分。

图1 1950-2007年我国农业受灾面积的变化

假设灾害发生强度为D(t)，从长时间看，灾害发生强度的变化既包含有确定的一面，也包含有随机的一面，确定的部分表现为某种趋势T(t)和周期规律P(t)，随机部分可视为在有限的状态之间转移，表现为随机波动成分S(t)。于是混合预测模型可表达为D(t)=T(t)+P(t)+S(t)，t=1，2，3，…。

因此可用混合预测模型作为受灾面积预测公式，建立动态模型并预测未来状态。首先通过建立t=1，2，…，55(即1950-2004年)的混合预测模型，预测 t=56，57，58(即 2005，2006和2007年)的发生值，并和这3年的统计值作比较，通过对比来检验模型的准确度。

2 趋势项的拟合——非线性回归模型

一般用一元非线性回归来拟合趋势项，一元线性回归x(t)=a+bt为一元非线性回归的基础。为了能够应用一般最小二乘法，需要把一般非线性模型x(t)=F(t，a，b)转化为某种线性形式。转换后的一般式为X(t)=A+BT。

其中变换式X(t)=Fx［x(t)］，A=Fa［a］，B=Fb［b］，T=Ft［t］。例如模型 x(t)=a ebt，两边取对数，就可变换为线性形式，其中X(t)=ln(x(t))，A=ln(a)，B=b，T=t。然后可按一元线性回归模型，通过最小二乘法计算出其中参数A，B，T，最后进行代换，计算出 a，b，t，把参数代入原表达式，就可以建立趋势项拟合模型［1］。

3 周期规律的提取——三角函数逼近

由混合预测模型可知，周期成分与随机波动的迭加为原始受灾面积数据D(t)与趋势项预测值之差，从图2中可以看出，绘制的数据折线图显示了该差值序列具有一定的周期性，考虑周期可能存在迭加，可采用三角函数P(t)=C+A sin(ω1+φ1)+B cos(ω2+φ2)，对周期分量数据进行拟合。式中A，B为波动幅度，C为直流成分，ω，ω1，ω2为频率，φ，φ1，φ2为初始相位。由于表达式是非线性的，所以无法利用线性回归来估计参数模型［2］。

确定部分包含趋势项T(t)和周期规律P(t)，把趋势项T(t)和周期项P(t)迭加在一起组成一个确定部分模型，计算结果为:

Q(t)=T(t)+P(t)=1 115.416t0.380+115.786+594.935sin(0.354t+4.368)-462.591cos(0.628t+2.706)。

图2 周期成分和随机波动迭加折线的变化

4 随机成分的评估——马尔科夫链

设有随机过程{Xn，n∈T}，若对于任意的整数n∈ T和任意的 i0，i1，…in+1∈ I，条件概率满足P{Xn+1=in+1|X0=i0，X1=i1，…，Xn=in}=P{Xn+1=in+1|Xn=in}，则称{Xn，n∈T}为马尔科夫链，简称马氏链。马尔科夫链是一种时间离散、状态可数的无后效随机过程，当前的状态和状态转移概率矩阵决定着下一个状态。利用马尔科夫链预测状态转移趋势的步骤可以分4个环节，分别为:状态划分、状态转移矩阵的建立、初始状态概率向量的建立、状态转移预测［3-4］。

4.1 状态划分

根据我国农业自然灾害受灾面积的随机波动情况，可以把随机扰动程度划分为5个状态 (表1)。根据预测波动值等于状态取值区间的平均值和确定部分预测值的乘积，计算出每一年的波动预测值，从图3中可以看出混合模型预测值已经拟合得非常好。

4.2 状态转移概率矩阵的建立

条件概率pij(n)=P{Xn+1=j|Xn=i}为马尔科夫链{Xn，n∈T}在时刻n的一步转移概率，其中i，j∈I。相当于随机游动的质点在时刻n处于状态i的条件下，下一步转移到状态j的概率，状态转移概率矩阵是对离散马尔科夫过程状态转移的定量描述［5］。其一步转移概率矩阵 P1= ［pij］n×n的计算公式为 Pij=Nij/Ni，i，j=1，2，…，n。

表1 随机波动的状态划分

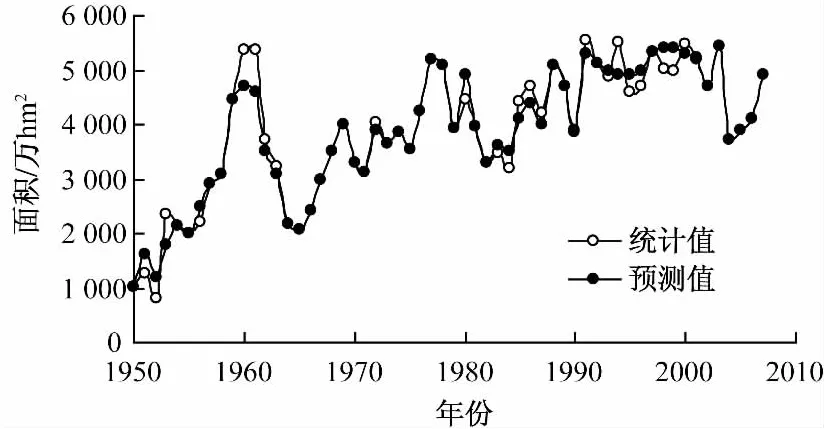
图3 受灾面积和混合模型预测值折线的变化

式中，Ni为序列中出现第i状态的次数，Nij为Ni个状态i中前一年状态为i，下一年状态为j的次数。同理可以建立k步状态转移概率转移矩阵Pk。且有如下的关系:

Pk=P1k及 Pk=P1Pk-1，k=1，2，… 。

根据我国农业自然灾害随机状分量划分的状态(表1)，可以得出1-4步的转移矩阵:

4.3 波动值的预测

设某一时刻状态分布矩阵为At，则状态预测模型:

At+k=AtPk，k=1，2，… 。

以此可计算出未来每一年各种灾害状态出现的概率，从而可确定随机分量的值，2002，2003，2004年随机分量的划分状态为3，5，2，即状态分布向量分别为，A2002=［0 0 1 0 0］，A2003=［0 0 0 0 1］，A2004= ［0 1 0 0 0］，预测计算结果列于表2，其中波动预测值等于用来预测年份的确定部分和状态区间平均值的乘积。

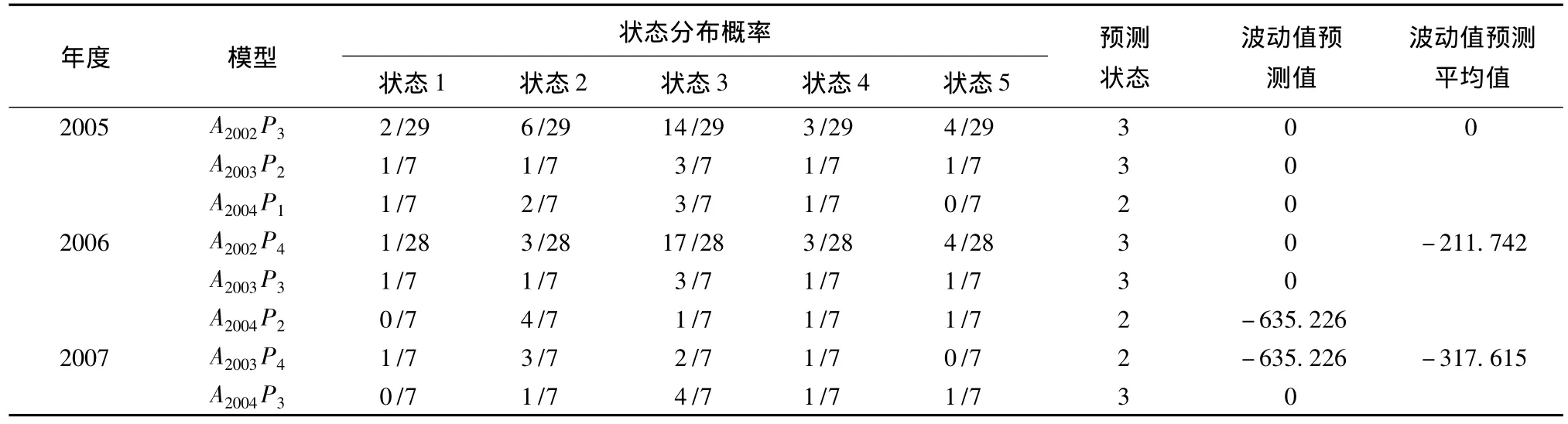
表2 波动值预测

5 预测模型的检验

把上述建立的3类模型迭加起来，可得到我国农业自然灾害集成预测模型:

D(t)=115.786+1 115.416t0.380+594.935sin(0.35t+4.368)-462.591cos(0.628t+2.706)+波动预测值。

当 t=1，2，…，55 时，可 以 计 算 出 1950，1951，…，2004年的我国农业自然灾害拟合值;当t=56，57，58时，可以计算出2005，2006，2007年的农业自然灾害预测值。和2005，2006，2007年的实际值对比 (表 3)，相对误差分别为10.77%，3.03%，8.39%，2006年的预测结果较好，2008年的尚可，2005年的则不太理想。

表3 模型预测值与实际发生值的比较

6 小结

我国是每年发生农业灾害较多且受灾面积较大的国家，对农业受灾面积的准确预测是农业可持续发展条件之一。但农业受灾面积变化受多种因素的影响，且诸多因素之间是一种多变量、强耦合、严重的非线性关系，这种关系具有动态性。传统的预测模型多数基于最小二乘法的单一数学公式，因而传统的一些预测方法精度不高。本研究模拟结果表明，用集成预测模型预测我国自然灾害的方法优于传统的单一数学模型。

［1］ 魏瑞江.河北省主要农作物农业气象灾害灾损评估方法［J］.中国农业气象，2000，21(1):27-31.

［2］ Park M W，Kim Y D.Asystematic procedure for setting parameters in simulated annealing algorithms ［J］.Computer＆Operations Research，1998，25(3):207-217.

［3］ 张颖.软计算方法［M］.北京:科学出版社，2002.

［4］ 宫德吉，陈素华.农业气象灾害损失评估方法及其在产量预报中的应用［J］.应用气象学，1999，27(1):66-69.

［5］ 赵素英，刘艳.应用灰色模型进行初、终霜灾害预测［J］.黑龙江八一农垦大学学报，17(3):31-38.